18.Нормальн.З-н распред.Непрер.Св.Вероятн.Попад.Знач.Норм.Случ.Величины в зад.Полуинтервал.

Непрер.СВ Х назыв.распред.по норм.з-ну если её функция плотн.вероятн.имеет вид:f(x)= * .Где σ,а параметры распред. σ>0.Вероятн.смысл параметров норм.распред.сост.в том,что а=М(Х). σ= σ(Х).Кратко норм.распред.с пар-ми а и σ запис.в виде Х €N(а; σ).График функ.(1)назыв.кривой.норм.распред.или кривой Гаусса.Исслед.функц.(1)показ.что эта функц.определена и положит.на всеё чисовой прямой.При х→+-∾,f(x)→0,т.е.ось Ох явл.горизонт.асимптотой.Функц.f(x) в т.х равн.а достиг.мах.равного.f(a)max= .Кривая норм.распред.симметрична относит.прямой х=а и имеет перегиб в точках с абциссами х=а- σ.х=а+ σ(рисунок).При изменении параметра а и пост. σ.форма кривой не меняется при этом кривая перемещается вдоль оси Ох.(с увелич.а график сдвиг.вправо,а при уменьш.влево).При изменении параметра σ меняятся форма норм.кривой(с уменьш. Σ кривая станов.всё более островершинной)Площадь,заключ.под кривой норм.распред.всегда=1.Функция распред.СВ Х распред.по норм.з-ну=F(x)= dt.Вероятность попадания значений норм.СВ Х в полуинтервал [α,β]т.е.Р(α≤х≤β)=Ф( )-Ф( .В частности вероятн.Р( того,что СВ Х€N(a,δ)отклонится от её матем.ожид.а по абсолютн.величине меньше некотор.положит.числа δравна=Р (( )=2Ф( ).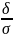

19.Правило трех сигм Преобразуем формулу     P([X-a]<δ)=2Ф( )Введем обозначение t=δ/σ,δ=tσТогда получим:P([X-a]<tσ)=2Ф(t)Если t=3, то P([X-a]<3σ)=2*0,49865=0,9973т. е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973. Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027=1-0,9973. Это означает, что лишь в 0,27% случаев так может произойти. Такие события, исходя из принципа невозможности маловероятных событий можно считать практически невозможными. В этом и состоит сущность правила трех сигм: Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математиче­ского ожидания не превосходит утроенного среднего квадратического отклонения. На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.

20.Функция одной случайной величины.Матем.Ожид.Функц.Одной св

Может оказаться что одна СВ У связана с другой СВ Х функц.зависимостью.Если каждому возм.значению СВ Х соотв.одно возможн.значение СВ У,то СВ У назыв.функц.СВ Х:У= φ(Х).Покажем как найти зак-н распред.СВ У по известному закону распред.СВ Х задан.рядом распределенй .Событие Х=х_i проис.с вероятн.p_i с этой же вероятн.СВ У примет значен.y_i= φ(x_i)Если разл.возможн.значением аргумента Х соотв.разл.значения функц.У,то вероятности соотв.значений Х,У равны между собой.Если же разл.возм.значен.СВ Х соотв.значен.СВ У среди котор.есть равные между собой,то вероятн.повтор.значений СВ У складывают.Если СВ Х явл.непрерывной с плотн.распред.f(x) и нам треб.найти распред.У= φ (Х),то польз.утвержден.:если функц.y=f(x) дифференц.строго возраст.;строго убывающ.обратн.функц.котор.х= Ψ(у),то плотность вероятн.д(у) СВ У наод.по формуле :д(у)=f[Ψ(y)] Ψ^’(y))-1. Матем.ожид.функц.одной СВ.Пусть задана У= φ(Х) и треб.найти матем.ожид.этой функц.зная закон распред.её аргумента Х.Если Х дискретная СВ задан.рядом распред.,то СВ У = φ(Х) будет также дискретной с возм.значен. φ(x_i)=y_i,i=1, ,котор.соотв.вероятности p_i следоват.матем.ожид.функции У= φ(Х)опред.формулой:М(У)=М(φ(Х))= .В случае когда СВ Х непрерывн.имеющ.плотность вероятн.f(x),для нахожд.матем.ожид.функц.У= φ(Х) можно сначало найти по формуле плотн.вероятн.а затем воспольз.рав-вом М(У)= ,а можно вычслить матем.ожид.по формуле:М[u(X)]= .