1.Предмет теории вероятности

ТВ – раздел матем-ки изуч-щий закон-ти однородных массовых случ явл-й.

В т.в. часто треб-ся из конечного мн-ва объектов произв природы наз-х элементами образовать отд мн-ва отлич-щихся друг от друга либо порядком располож-я эл-тов либо самими эл-тами. Эти мн-ва наз-т соединениями а подсчётом их кол-ва и занимается комбинаторика. Перестановками из данных эл-тов наз соединения из этих n-эл-тов различ-щиеся только порядком. Общее число всех перестановок из n-эл-тов вычисл-ся по ф-ле: ;

Размещениями из данных n-эл-тов по k-эл-тов (0<k≤n) наз такие соединения каждое из к-рых содержит k-эл-тов из данных n-эл-тов и отлич-ся от любого другого либо составом эл-тов либо порядком располож-я эл-тов. Общее число 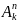в размещении из n-эл-тов по k-эл-тов вычисл-т по ф-ле: ;

Сочетаниями из n-эл-тов по k (0<k≤n) наз такие соединения каждое из к-рых содержит k-эл-тов из данных n-эл-тов и отлич-ся от любого другого хотя бы одним эл-том. Общее число разл сочетаний из n-эл-тов по k вычисл-т по ф-ле: ;

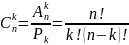Для сочетаний справедливы нерав-ва:

1) = (св-во симметричности),

2) (правило Паскаля);

2 Важных правила комбинаторики:

1) правило умнож-я: если треб-ся выполнить одно за др какие-то k действий к-рые можно выполнить соотв-но сп-бами то все k действия могут быть выполнены 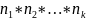сп-бами;

2) правило сложения: если 2 взаимноисключ-щие друг друга действия могут выполн-ся соотв-но m или n сп-бами то выполнить одно любое из этих действий можно m+n сп-бами.

2. События и их классификация

Под опытом или экспериментом или испытанием будем понимать всякое осущ-ние комплекса усл-й или действий при кот наблюд-ся соотв-щее явл-е. Возможным рез-том опыта наз событием. Событие наз достоверным если оно произойдёт обяз-но при испытании. Невозможным наз-ся событие, которое никогда не может произойти ни при одном из совершаемых испытаний. Случайным называется событие, которое при осуществлении некоторой совокупности условий может либо произойти, либо не произойти. Два события наз совместными в данном опыте если появл-е одного из них не исключает возм-ть появл-я другого, и несовместными – в противном случае. Неск-ко событий в данном опыте наз папарно несовместными если любые 2 из них несовместные. Полная группа событий - это папарно несовместные события и при каждом испытании происходит одно из них (и только одно). Два события образ-щую полную группу наз противоположными. Равновозможными наз события когда нет основания полагать что одно из них явл более возможным чем другие.

3 Соотнешения между событ-ми.

Суммой событий А и В называется событие С = А + В, состоящее в наступлении по крайней мере одного из событий А или В. Произведением событий А и В называется событие С = А В, состоящее в том, что в результате испытания произошли и событие А, и событие В.Раз-ю 2х событ А и Б наз такое событ С,кот сост в совместном наступ соб А и ненаступ соб В.Теорема1:вер-ть суммы 2х несовмест событ А и В =сумме их вер-й,т е:Р(А+В)=Р(А)+Р(В).Следствие 1:сумма вер-й событий образ полн группу =1.След2:сумма вер-й противопол соб=1.Теорема2:вер-ть суммы 2х совместных соб А и В=сумме их вер-й без вер-ти их совместн наступ.т е:Р(А+В)=Р(А)+Р(В)-Р(АВ).Теорема3:вер-ть произвед 2х событ А и В =произвед вер-й одного из них на условн вер-ть друго:Р(АВ)=Р(А)Р( ),Р(АВ)=Р(В)Р( )

4Классическое опред-е: Всевозможные исключ-щие друг друга рез-ты одного испытания наз элементарными исходами. Пусть - полная группа равновозможных исходов испытания. При некот исходах соб-е А наступает, а в др – не наступает. Исходы, при кот соб-е А наступает, благоприятствует соб-ю А.Вероятностью соб-я А наз отношение числа m элемент исходов благоприятствующих соб-ю А к числу n всех равновозможных и образующих полную группу элемент исходов т.е. ;

Из опред-я вер-ти след-т св-ва:

1) P (U) = = 1 - вероятность достоверного события равна единице; 2) P (V) = = 0 - вероятность невозможного события равна нулю; 3) 0<P (A)<1 - вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Статистич опред-е: Относит частотой (частностью) соб-я А наз отнош-е числа m опытов в кот появ соб-е А к числу n всех проведённых опытов т.е. .

Оказыв-ся что по мере увел-ния числа испытаний n относит частота соб-я А измен-ся мало, устойчиво колеблясь при этом около некот постоянного числа р кот берут за стат вер-ть. На практике обычно за стат вер-ть берут его относит частоту и польз-ся приближ рав-вом:

5.Геометрич. вер-ть. Геометр. определ-е вер-ти прим-ся, когда исходы опыта равновозможны. Геометр. вер-тью соб. А назыв. отнош-е площади области D к площади обл. U. геометр. определ-е вер-ти события применимо и в случае когда области U и D обе линейные или объёмные Св-ва геометрич. вер-ти: 1)0<=P(A)<=1;2)P(V)=0; 3)P(U)=1; P(A+B)=P(A)+P(B)