31) Сформулировать метод северно-западного угла транспортной задачи.

Заполнение начинается с клетки (1,1) и на каждом следующем шаге заполняется верхняя левая (северо-западная) клетка среди невычеркнутых клеток. Недостатком этого метода является то, что он не учитывает значения тарифов c_ij.

32) Сформулировать метод минимальной стоимости транспортной задачи.

Метод минимальной стоимости

Метод минимальной стоимости прост и позволяет построить опорное решение, достаточно близкое к оптимальному, так как использует матрицу стоимостей транспортной задачи C=(cij).

Как и метод северо-западного угла, он состоит из ряда однотипных шагов, на каждом из которых заполняется только одна клетка таблицы, соответствующая минимальной стоимости: и исключается из рассмотрения только одна строка (поставщик) или один столбец (потребитель). Очередную клетку, соответствующую , заполняют по тем же правилам, что и в методе северо-западного угла. Поставщик исключается из рассмотрения, если его запасы груза использованы полностью. Потребитель исключается из рассмотрения, если его запросы удовлетворены полностью. На каждом шаге исключается либо один поставщик, либо один потребитель. При этом если поставщик еще не исключен, но его запасы равны нулю, то на том шаге, когда от данного поставщика требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль и лишь затем поставщик исключается из рассмотрения. Аналогично с потребителем.

33)Сформулировать алгоритм метода потенциалов транспортной задачи.

1. Определяют модель транспортной задачи. В случае открытой модели переходят к закрытой, вводя либо фиктивного поставщика, либо фиктивного потребителя.

2. Одним из методов проводят первоначальное распределение поставок. При этом должно быть заполнено ровно m+n-1 клеток, где m – число поставщиков, n – число потребителей с учетом фиктивных, если они есть.

3. Находят потенциалы поставщиков u_i и потенциалы потребителей v_j , решая систему уравнений v_j-u_i=c_ij для всех заполненных клеток. Эта система содержит m+n неизвестных и m+n-1 уравнений. Поэтому полагают, что одна из неизвестных ( обычно u₁) равна нулю.

4. Находят матрицу оценок клеток G с элементами g_ij = v_j-u_i-c_ij. Отметим, что оценки заполненных клеток должны равняться нулю. Возможны следующие случаи:

1) в матрице оценок нет положительных значений. В этом случае, полученное распределение поставок является оптимальным и минимальные затраты составят F _min = 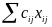( по заполненным клеткам). Отметим, что, если только заполненные клетки имеют нулевые оценки, то задача имеет единственное решение. В противном случае, задача имеет несколько решений.

2) в матрице оценок имеются положительные значения. Выбираем клетку с наибольшей положительной оценкой. Для этой клетки строят цикл перераспределения поставок, определяют объем перемещаемой постав и проводят перераспределение поставок. После этого переходят к пункту 3.

34)Что называется целочисленным программированием?

Целочисленное программирование – один из наиболее молодых, перспективных и быстро развивающихся разделов математического программирования. Можно перечислить большое количество разнообразных задач планирования экономики, организации производства, исследования конфликтных  ситуаций, синтеза схем автоматического регулирования, которые формально сводятся к выбору лучших, в некотором смысле, значений параметров из определенной дискретной совокупности заданных величин. К ним можно отнести и экстремальные комбинаторные задачи, возникающие в различных разделах дискретной математики.

Задачи и методы, относящиеся к перечисленному кругу вопросов, в литературе именуются по-разному. Наибольшее распространение получил термин «целочисленное программирование», однако встречаются и такие как «дискретное программирование», реже «комбинаторное (или диофантово) программирование».

Наиболее изученными задачами этого класса являются целочисленные задачи линейного программирования, в которых на все переменные (или на их часть) наложено дополнительное требование целочисленности. От них принято отличать так называемые дискретные задачи линейного программирования, в которых область допустимого изменения каждой переменной – не множество целых неотрицательных чисел, а некоторое заданное конечное множество.

Целочисленные задачи математического программирования могут возникать различными путями.

1. Существуют задачи линейного программирования, которые формально к целочисленным не относятся, но при соответствующих исходных данных всегда обладают целочисленным планом. Примеры таких задач – транспортная задача и ее модификации (задачи о назначениях, о потоках в сетях).

2. Толчком к изучению целочисленных задач в собственном смысле слова явилось рассмотрение задач линейного программирования, в которых переменные представляли физически неделимые величины. Они были названы задачами с неделимостью. Таковы, например, задачи об оптимизации комплекса средств доставки грузов, о нахождении минимального порожнего пробега автомобилей при выполнении заданного плана перевозок, об определении оптимального машинного парка и его оптимального распределения по указанным работам при условии минимизации суммарной стоимости (машинного парка и производимых работ), о нахождении минимального количества судов для осуществления данного графика перевозок и т. п.

3. Другим важным толчком к построению теории целочисленного программирования стал новый подход к некоторым экстремальным комбинаторным  задачам. В них требуется найти экстремум целочисленной линейной функции, заданной на конечном множестве элементов. Такие задачи принято называть задачами с альтернативными переменными. В качестве примеров можно назвать задачи коммивояжера (бродячего торговца), об оптимальном назначении, теории расписания, или календарного планирования, и задачи с дополнительными логическими условиями (например, типа «или – или», «если – то» и т. п.)

35) . Сформулировать метод Гомори (отсечений).

алгоритм гомора линейное программирование

Введем правильного отсечения, которое лежит в основе многих численных методов решения целочисленных задач линейного программирования.

Определение 2. Пусть x* - оптимальный план задачи (1.1), (1.2), не являющийся целочисленным. Неравенство

где g = (g1, g2, …, gn), называется правильным отсечением, если оно удовлетворяет требованиям:

а) для вектора x* неравенство не выполняется, т.е. <g, x*> > g0 (условие отсечения).

б) если x - целочисленный план задачи (1.1), (1.2) ( т.е. план задачи (1.1)-(1.3)), то x - удовлетворяет (3.1) (условие правильности).

Понятно, что добавление неравенства (3.1) к условиям (1.1), (1.2) сужает допустимое множество X, сохраняя при этом все его целочисленные точки. Тем самым последовательное применение этого приема дает как бы многоэтапную аппроксимацию многогранника Xz с помощью линейных ограничений.

В связи с понятием правильного отсечения возникают две проблемы. Первая из них состоит в том, что бы сформулировать общий алгоритм отсечения для произвольной целочисленной задачи линейного программирования. Вторая проблема состоит в построении правильного отсечения таким образом, что бы обеспечить решение задачи (1.1)-(1.3) за конечное число шагов, т.е. чтобы от множества X всякий раз отсекались достаточно большие участки.

Отметим, что второе требование является довольно тонким. В качестве подтверждения рассмотрим способ построения правильного отсечения, предложенный Данцигом.

Пусть x* - опорный оптимальный план задачи (1.1), (1.2), s и w - списки номеров соответственно базисных и не базисных переменных, отвечающих некоторому базису плана x*. Тогда xj* = 0 при jÎw. С учетом этого свойства нетрудно построить правильное отсечение для плана x*, если он является не целочисленным: в качестве такого может служить неравенство

.

В самом деле, условие отсечения тривиально выполняется, поскольку . Условие правильности так же соблюдено, так как если x = (x1, x2 , …, xn) - целочисленный план задачи (1.1), (1.2), то величина с учетом условий xj ³ 0, jÎw, может быть меньше единицы лишь в том случае, когда xj = 0 при всех jÎw. Но в таком случае план x - опорный, и в качестве его базиса можно принять базис плана x*. Опорный план однозначно определяется своим базисом, откуда получаем, что из неравенства вытекает x=x*. Последнее, однако, невозможно, так как x - целочисленный вектор, а x* таковым не является.

Указанный прием построения правильного отсечения, несмотря на его простоту, оказался малоэффективным, поскольку конечность процесса решения обеспечивается лишь для узкого класса целочисленных задач линейного программирования.

36) Что называется  теорией игр?

Построением математических моделей конфликтных ситуаций и разработкой методов их решений занимается теория игр.

Теория игр – это теория математических моделей принятия оптимальных решений в конфликтных ситуациях.

Конфликтную ситуацию будем называть игрой, а участников конфликтной ситуации игроками. В игре могут сталкиваться интересы двух или нескольких противников, поэтому игры разделяются на парные и множественные. Если во множественной игре интересы некоторых игроков совпадают, то они могут объединяться в коалиции. Такие игры называются коалиционными.

37) Что такое игра?

Конфликтную ситуацию будем называть игрой, а участников конфликтной ситуации игроками. Результатом каждой игры является тот или иной выигрыш. В теории игр выигрыш имеет числовое значение (чаще всего в денежных величинах). Величина выигрыша является функцией стратегий, выбранных игроками.

38) Какие игры называются парными, множественными, коалиционными, конечными, бесконечными, антагонистическими (играми с нулевой суммой)?

В игре могут сталкиваться интересы двух или нескольких противников, поэтому игры разделяются на парные и множественные. Если во множественной игре интересы некоторых игроков совпадают, то они могут объединяться в коалиции. Такие игры называются коалиционными.

Для достижения поставленных целей каждый из игроков принимает те или иные решения. Каждое из таких решений в теории игр называется стратегией игрока. Количество стратегий у каждого игрока может быть конечным или бесконечным, в зависимости от этого игры подразделяются на конечные и бесконечные. В дальнейшем мы будем рассматривать конечные игры. Пример бесконечной игры – “продавец-покупатель”. Стратегии продавца – назначение цены товара, стратегии покупателя – количество покупаемого товара.

Результатом каждой игры является тот или иной выигрыш. В теории игр выигрыш имеет числовое значение (чаще всего в денежных величинах). Величина выигрыша является функцией стратегий, выбранных игроками. Эту функцию называют функцией выигрыша или платежной функцией. Важный класс игр составляют игры, в которых выигрыш одного игрока равен проигрышу другого игрока. Такие игры называются антагонистическими или играми с нулевой суммой. Прямой противоположностью таких игр являются игры с постоянной разностью, в которых игроки и выигрывают, и проигрывают одновременно, так что им выгодно действовать сообща. Между этими крайними случаями имеется множество игр с ненулевой суммой, где имеются и конфликты, и согласованные действия игроков.

39) какая матрица называется платежной матрицей (матрицей выигрышей)?

Результатом каждой игры является тот или иной выигрыш. В теории игр выигрыш имеет числовое значение (чаще всего в денежных величинах). Величина выигрыша является функцией стратегий, выбранных игроками. Эту функцию называют функцией выигрыша или платежной функцией. Важный класс игр составляют игры, в которых выигрыш одного игрока равен проигрышу другого игрока. Такие игры называются антагонистическими или играми с нулевой суммой.