7. Реактор идеального вытеснения (рив) и его характеристическое уравнение

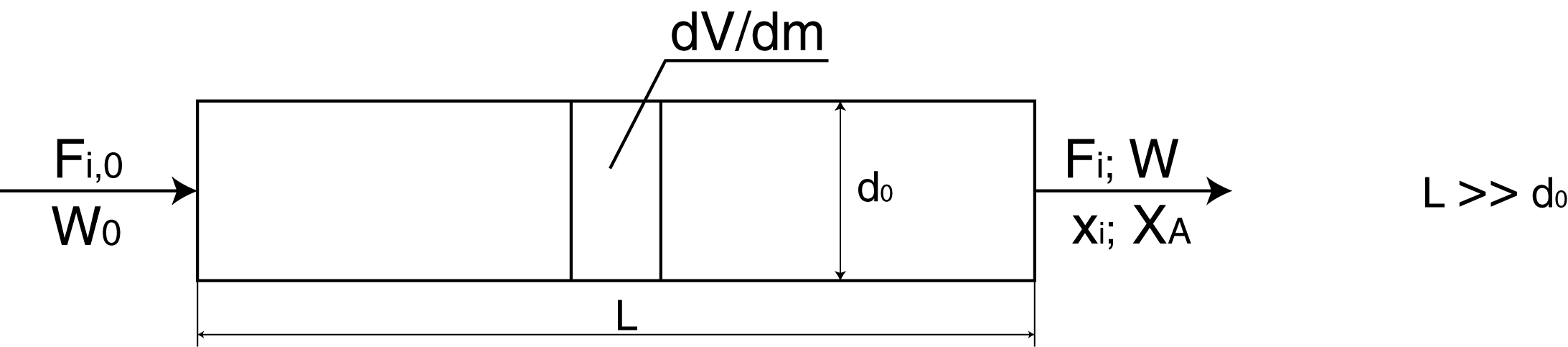
Рис. 7.1. Схема реактора идеального вытеснения.

Реактор идеального вытеснения (рис. 7.1) является моделью непрерывно действующих аппаратов вытеснения, в которых реакционная масса движется вдоль оси, вытесняя последующие слои.

Условием идеальности РИВ является отсутствие продольного перемешивания. В стационарных условиях при постоянстве скорости подачи и состава исходной смеси, а также при постоянстве условий теплообмена каждый элемент пребывает в таком реакторе в течении одинакового времени, а концентрация и температура в каждом поперечном сечении остаются постоянными. При этом, в отличие от периодического реактора, концентрация веществ изменяется не во времени, а по длине реактора (рис. 7.2).

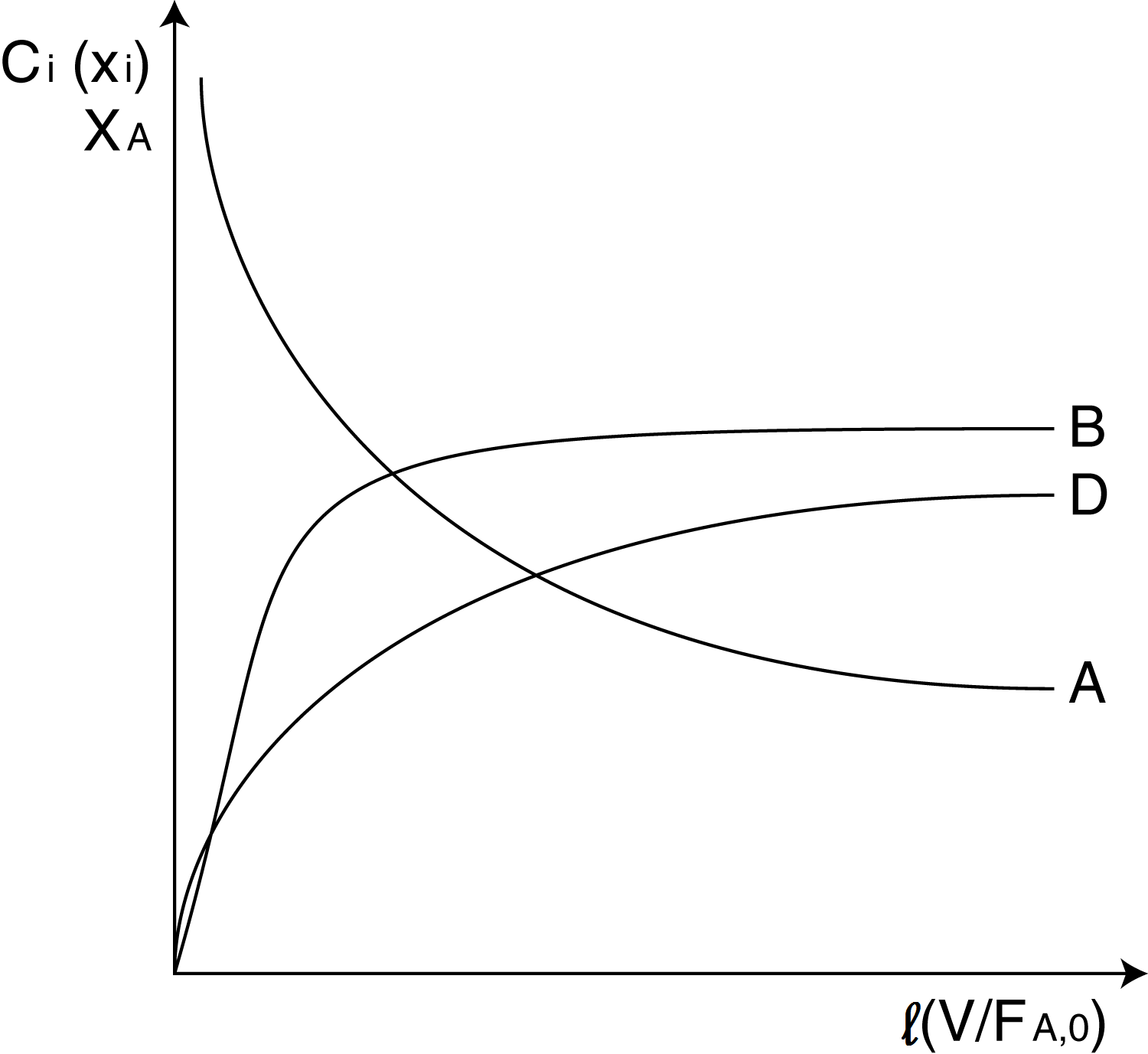
Рис. 7.2. Концентрационные кривые реактора идеального вытеснения.

l – величина обратная мольной нагрузке на единицу мольного объёма в единицу времени. Это позволяет составить уравнение материального баланса для бесконечно малого элемента объёма, поперечного потоку реагентов:

dF_i = r_i ∙ dV;

это следует из уравнения (4-4).

7.1. Гомогенные реакции. После разделения переменных интегрирования получим общее характеристическое уравнение:

; (7-1)

Уравнение (7-1) можно записать для субстрата А:

; (7-2а)

dF_A,0 = –F_A,0  dX_A

Разделим обе части уравнения (7-1) на W₀:

; (7-2)

V – объём;

W₀ – объём/время;

(V/W₀) = r_ист – истинное время контакта.

;

В уравнении (7-2) V/W₀ имеет размерность времени и при отсутствии насадки в реакторе или за вычетом её объёма равно истинному времени контакта.

Очевидно, что в этом случае уравнения (6-3) и (7-2) для периодического реактора и реактора вытеснения соответственно полностью совпадают. Более общую форму уравнения для РИВ верную и для изменяющего объема смеси можно вывести изменяя F_i в уравнении (7-1) через химические выходы ключевых веществ.

;

Это из уравнения (2-6) при условии, что F_i,0 = 0

Подставив значение F_i в уравнение (7-1) получим:

; (7-3)

Это уравнение годится и для основного реагента A, если полагать, что его выход x_A = 1 – X_A.

В левой части уравнения (7-3) находится величина обратная мольной нагрузке единицы объема реактора по основному реагенту в единицу времени и имеющая размерность:

V/F_A,0 = [(объем)(время)(моль)^–1];

Эта величина называется условным временем контакта и является временной характеристикой гомогенных непрерывных процессов, заменяющей время реакции при периодических условиях.

7.2. Гетерогенно-каталитические реакции. Для гетерогенно-каталитических реакций материальный баланс можно составить для микромассы катализатора.

dF_i = r_idm_K;

Разделив переменные, выведем характеристические уравнения:

; (7-4)

Разделим обе части на W₀:

;

Отсюда можем выразить характеристическое уравнение гетерогенно-каталитических реакций:

; (7-5)

Чаще всего используют уравнение. в левой части которого находится величина, обратная мольной нагрузке единицы массы катализатора по основному реагенту в единицу времени и имеющая размерность:

F_А,0/m_K = [(масса)(время)(моль)^-1]

Эту величину также называют условным временем контакта и она является временной характеристикой непрерывных гетерогенно-каталитических реакций. Хотя она и не имеет размерности времени.

В технологии используют ещё одну временную характеристику, а именно объёмную скорость [u] = [(время)^-1]. Если её выражать по объёму всей поступающей смеси, приведенному к условиям в реакторе, то u=W/V, т.е. объёмная скорость равна объёмной нагрузке единицы реакционного объёма, в единицу времени. Тогда при неизменности объёма смеси во время реакции u = τ ^–1_ист. Объёмную скорость применяют и для характеристики гетерогенно-каталитических процессов, относя её к насыпной массе катализатора. Кроме того, её часто выражают по объёмному потоку не всей смеси, а только основного реагента и при том в нормальных условиях.

РИВ применяют для кинетических исследований реакций в потоке, особенно для газофазных процессов, в том числе гетерогенно-каталитических. К условиям идеального вытеснения близки аппараты большой длины и малого диаметра. Поэтому реактор изготавливают в виде трубки или змеевика, имеющих карманы для термопары. Для обеспечения постоянной температуры по длине реактора и диаметру его термостатируют. Ввиду трудностей с теплообменом в этом типе реактора допускается регулирование температуры с пониженной точностью до 12C. Перед началом каждого опыта через реактор пропускают 35 объёмов реакционной смеси, чтобы в аппарате установился стационарный режим. После этого накапливают пробу продуктов и анализируют её тем или иным методом. Начинают следующий опыт при других параметрах процесса, т.о. каждый опыт даёт только одну экспериментальную точку. По сравнению с периодическим условием здесь большая длительность и трудоёмкость исследований. В РИВ варьируют те же параметры, но вместо времени изменяют условное время контакта (V/F_A,0 и m_K/F_A,0 ) Экспериментальные данные сводят в таблицы или представляют в виде кинетических кривых в координатах:

x_i^A(X_A, C_i) – V/F_A,0(m_K/F_A,0).