4. Скорость превращения веществ, скорость реакции и кинетические уравнения

Кинетический метод является универсальным для количественного изучения химических реакций. Кинетический метод используется в двух направлениях:

Теоретическом – для выяснения механизмов реакции и реакционной способности реагентов.

Практическом – для расчетов химических реакторов и оптимизации химических процессов.

4.1. Периодические реакции. Скорость превращения любого вещества для гомогенных реакций определяется уравнением:

; (4-1)

n_i – количество вещества (моль; кмоль);

t – время (с; мин; ч);

V – объем (мл; л; м³);

При постоянстве реакционного объема объем можно ввести под знак дифференциала. Тогда получим концентрационное выражение скорости превращения вещества i:

; (4-2)

Для гетерогенных реакций скорость превращения вещества обычно относят к единице массы катализатора:

; (4-3)

m_К – масса катализатора.

4.2. Непрерывные процессы. Для непрерывных процессов в стационарных условиях скорость превращения веществ определяется, как производная их мольных потоков по реакционному объему для гомогенных реакций или по массе катализатора для гетерогенно – каталитических реакций

; (4-4)

; (4-5)

Поскольку F_i измеряют в молях (кмолях)/время, то размерность этих скоростей совпадет с размерностью r_i в уравнениях (4-2) и (4-3).

Для любой реакции справедливо соотношение (1-1), которое можно записать в дифференциальной форме:

;

;

Разделим эти равенства на значение Vdt, dt, dV, или dm_К, то получим:

; (4-6)

В отличии от скорости превращения вещества r_i величина r независима относительно участников реакции и всегда положительна . Это и есть скорость химической реакции связанная со скоростью превращения вещества для простых реакций соотношением:

r_i = ν_i·r;

Для сложной системы превращений, каждая из простых реакций имеет некоторую скорость r_j:

; (4-7) - для гомогенных реакций

; (4-8) - для гетерогенных

_i,j  стехиометрический коэффициент вещества i для простой реакции j взятый с соответствующим знаком.

Из выражений (4-7) и (4-8) видно, что скорости реакции есть соответствующие производные полноты реакции. В сложных системах реакции каждое вещество может образовываться или расходоваться по нескольким простым реакциям, и тогда общая скорость его превращения будет связана со скоростью соответствующих реакций уравнением:

; (4-9)

Это выражение аналогично выражению (1-3).

Для описания дифференциального баланса системы нужно иметь такие уравнения только для ключевых веществ, однако в правой части уравнений нужно учитывать все простые реакций, а не только независимые, как это было при расчете баланса сложных реакций:

Пример:

Процесс гетерогенно-каталитической дегидратации этилового спирта протекает по реакции:

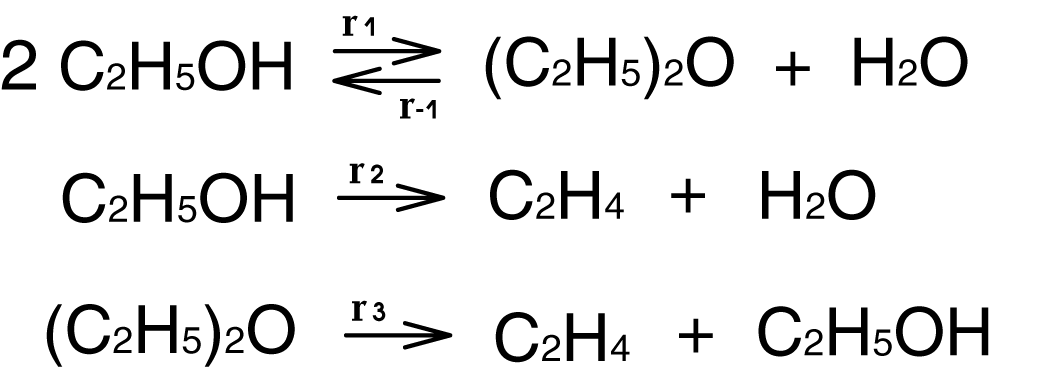
Требуется через скорости реакций записать скорость превращения ключевых веществ. В этой системе реакции имеется 2 ключевых вещества: диэтиловый эфир и этилен. Скорости превращения равны:

;

;

Скорость каждой простой реакции есть функция концентраций или парциальных давлений некоторых постоянных, к которым относятся константы скорости k_j, константы равновесия К_j и адсорбционный коэффициент b_i.

Константа скорости определяется уравнением Аррениуса:

; (4-10)

k_j,0 – предэкспоненциальный множитель;

E – энергия активации реакции;

Константы равновесия К_j определяется уравнением

; (4-11)

K₀ – предэкспоненциальный множитель;

Таким образом константы кинетического уравнения зависят от температуры.

Различные постоянные этого уравнения (k_j, K_j, E_j, b_j, k_i,0 и др.) называют параметрами химической реакции и обозначают через _j.

В отличии от этого внешние факторы, влияющие на скорость реакции, можно назвать параметрами химического процесса. Сюда относятся концентрация или парциальное давление, температура. Тогда выражение для скорости реакции можно записать в общем виде:

; (4-12)

Концентрационный вид этого уравнения может быть самым разнообразным, являясь следствием механизма реакций, материального баланса веществ и т.д.

Объединяем уравнения (4-9) и (4-12) получаем уравнение для скорости превращения вещества:

; (4-13)

В дифференциальной форме уравнение (4-13) описывается изменением количества вещества в зависимости от параметров реакций и условий процесса.

Совокупность уравнения скорости для всех ключевых веществ называют кинетической моделью процесса в стационарных условиях его проведения. Нахождение таких уравнений является задачами кинетического исследования. Основными этапами этого исследования являются:

1. проведение эксперимента.

2. выдвижение гипотезы о механизме реакций и построение уравнений на основе этого механизма.

3. обработка результатов эксперимента по этим уравнениям.

В действительности этапы последовательности нарушаются.