16. Интегральные методы исследования последовательных реакций

Из необратимых реакций этого типа наиболее интересны реакции первого порядка:

A₀ A₁ A₂ …;

и последовательно-параллельные превращения, имеющие общий второй реагент:

A₀ A₁ A₂ …;

К последовательно-параллельным реакциям относятся и реакции последовательного замещения атомов водорода при хлорировании, алкилировании и т.д:

Сюда же относят реакции последовательного присоединения к полиолефинам и ароматическим соединениям:

CH₂=CH–CH=CH₂ CH₃–CH=CH–CH₃ CH₃–CH–CH–CH₃

Последовательное удлинение молекулярной цепи при олигомеризации:

Рассмотрим кинетику последовательно-параллельных превращений имеющий общий второй реагент:

A₀ A₁ A₂ …;

Если стехиометрические коэффициенты и порядок реакции по реагентам каждой стадии для этой реакции равны единице, то при их необратимости получим для первого промежуточного продукта, что селективность равна:

; (16-1)

где С_А и С_В – текущие концентрации исходного реагента и первого промежуточного продукта.

Последнее выражение надо проинтегрировать. Для этого вводим вспомогательную переменную.

U = C₁/C₀;

C₁ = UC₀;

Интегрируем С₁ относительно С₀:

;

Приравняем правые части последнего уравнения и уравнения (16-1):

;

Из последнего равенства получаем:

;

Опустим минус для удобства, а потом его учтем. Проинтегрируем правую часть уравнения приняв в ней, что (k₁/k₀)  1 = 

Тогда:

;

;

Избавимся от логарифма:

;

Возведем левую и правую части уравнения в степень (k₁/k₀)  1:

;

;

;

Умножим обе части уравнения на (С₀/С_0,0)

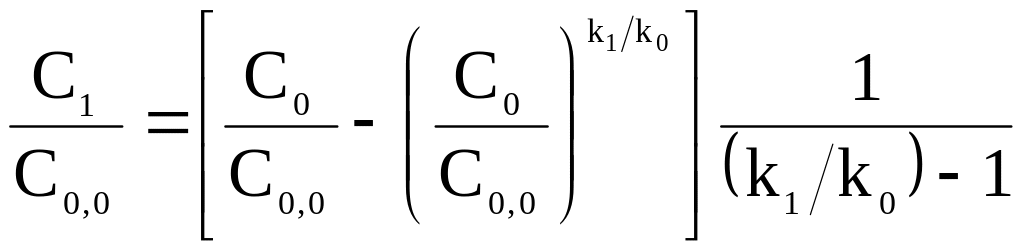; (16-2)

Заменим (С₀/С_0,0) на (1 – Х₀) и (С₁/С_0,0) на :

; (16-3)

; (16-4)

Таким образом, выход первого промежуточного продукта зависит от доли непревращенного исходного реагента или от (1Х_А) и от соотношения констант скорости соответствующих реакций. Это уравнение справедливо если (k₁/k₀)  1.

Если (k₁/k₀) =1, то справедливо другое выражение. Последовательно- параллельные реакции имеют некоторые важные особенности. Для них часто бывает, что второй реагент вначале превращается в активную промежуточную частицу (радикал или катион), которая атакует каждый из последующих образующих продуктов реакции. Причем эта элементарная стадия и определяет соотношение продуктов. В результате независимо от вида кинетического уравнения реакций оказываются справедливыми выведенные выше уравнения. Проиллюстрируем эти уравнения рис. 16.1

Рис.16.1. Зависимость состава продуктов и селективности последовательных реакций от степени конверсии.

Анализ полученной зависимости показывает, что по первому промежуточному продукту при Х_А  0, селективность , что является доказательством последовательной схемы превращения.

17. Исследование влияния температуры

Влияние температуры на состав продукта, селективность и скорость реакции проявляется через зависимость от нее параметров реакций, т.е констант скоростей, равновесия, адсорбционных коэффициентов, коэффициентов диффузии.

Уравнение зависимости константы скорости от температуры:

;

Зависимость константы равновесия от температуры:

;

Зависимость абсорбционных коэффициентов от температуры:

;

В этих реакциях величины k_j,0; K_j,0; b_i,0 – предэкспоненциальные множители

K_j,0 и b_i,0 – постоянные интегрирования, не имеющие физического смысла.

Для полной характеристики процесса при его исследовании необходимо найти предэкспоненциальные множители, энергию активации или энтальпии всех параметров, входящих в кинетическую модель. Последовательность исследований следующая:

1. В начале описанными выше методами при некой температуре находят концентрационные зависимости скорости и ее константы.

2. Считая, что модель сохраняет свой вид и при других температурах, проводят опыты при 2-х – 4-х других температурах, определяя соответствующие параметры.

3. После нахождения констант при нескольких температурах находят активационные параметры или энтальпию процесса по линеаризованной форме приведенных выше уравнений типа Аррениуса:

;

; (17.1)

;

Эти уравнения в координатах (lnk_j,0  1/T) ; (lnK_j,0  1/T) ; (lnb_i,T  1/T) дают линейную зависимость с тангенсом угла наклона E_j/R, H_j/R (рис.17.1)

Расчет значений lnk_j,0; lnK_j,0; lnb_i,0 проводят при помощи линейного МНК.

Рис.17.1. Линеаризация уравнения Аррениуса.

Доверительный интервал искомых величин находят обычным образом, устраняя в них лишние значащие цифры из предэкспоненциального множителя в уравнении Аррениуса, затем можно найти энергию активации.