Отметим, что в последнем случае адиабатический процесс называют изоэнтропийным процессом, т.К. .Термодинамическое определение энтропии

Понятие энтропии было впервые введено в 1865 году Рудольфом Клаузиусом. Он определил изменение энтропии термодинамической системы при обратимом процессе как отношение общего количества тепла   к величине абсолютной температуры   (то есть тепло, переданное системе, при постоянной температуре):

.

Например, при температуре 0 °C, вода может находиться в жидком состоянии и при незначительном внешнем воздействии начинает быстро превращаться в лед, выделяя при этом некоторое количество теплоты. При этом температура вещества так и остается 0 °C. Изменяется состояние вещества, сопровождающееся выделением тепла, вследствие изменения структуры.

Рудольф Клаузиус дал величине   имя «энтропия», происходящее от греческого слова τρoπή, «изменение» (изменение, превращение, преобразование). Данное равенство относится к изменению энтропии, не определяя полностью саму энтропию.

Эта формула применима только для изотермического процесса (происходящего при постоянной температуре). Её обобщение на случай произвольного квазистатического процесса выглядит так:

,

где   — приращение (дифференциал) энтропии некоторой системы, а   — бесконечно малое количество теплоты, полученное этой системой.

Необходимо обратить внимание на то, что рассматриваемое термодинамическое определение применимо только к квазистатическим процессам (состоящим из непрерывно следующих друг за другом состояний равновесия).

Поскольку энтропия является функцией состояния, в левой части равенства стоит её полный дифференциал. Напротив, количество теплоты является функцией процесса, в котором эта теплота была передана, поэтому   считать полным дифференциалом нельзя.

Энтропия, таким образом, согласно вышеописанному, определена вплоть до произвольной аддитивной постоянной. Третье начало термодинамики позволяет определить её точнее: предел величины энтропии равновесной системы при стремлении температуры к абсолютному нулю полагают равным нулю.

22. Второе начало термодинамики

Второе начало термодинамики может быть сформулировано несколькими способами. В наиболее очевидной формулировке второе начало гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому. Более строго, невозможны такие процессы, единственным конечным результатом которых был бы переход тепла от тела, менее нагретого, к телу, более нагретому.

Второе начало термодинамики может быть также сформулировано следующим образом: невозможны такие процессы, единственным конечным результатом которых явилось бы отнятие от некоторого тела определенного количества тепла и превращения этого тепла полностью в работу.

На первый взгляд может показаться, что второй формулировке противоречит, например, процесс изотермического расширения идеального газа. Действительно, все полученное идеальным газом от какого-то тела тепло превращается полностью в работу. Однако получение и превращение его в работу не единственный конечный результат процесса, кроме того, в результате происходит изменение объема газа.

Легко убедиться, что утверждение, содержащееся во второй формулировке, логически вытекает из утверждения, заключенного в первой формулировке. В самом деле, работа может быть полностью превращена в тепло, например, при трении. Поэтому, превратив с помощью процесса, запрещенного второй формулировкой, тепло, отнятое от какого-либо тела, полностью в работу, а затем превратив эту работу при посредстве трения в тепло, сообщаемое другому телу с более высокой температурой, мы осуществим  процесс, невозможный согласно первой формулировке.

Использую процессы, запрещаемые вторым началом термодинамики, можно было бы создать двигатель, совершающий работу за счет тепла, получаемого от такого, например, практически неисчерпаемого источника энергии, как океан. Практически  такой двигатель был бы равнозначен вечному двигателю. Поэтому второе начало иногда формулируется следующим образом: невозможен перпетуум мобиле второго рода, т.е. такой периодически действующий двигатель, который получал бы тепло от одного резервуара и превращал это тепло полностью в работу.

Согласно наиболее общей формулировке второго начала термодинамики, бесконечно малое кол-во тепла , переданное системе в обратимом процессе, отнесенное к абс. т-ре Т, является полным дифференциалом ф-ции состояния 5, наз. энтропией. Для обратимых процессов  dS; для необратимых  < dS. Для любых процессов (обратимых и необратимых) второе начало термодинамикиможет быть обобщено записью dS  . В изолированных (замкнутых) системах  и dS 0, т.е. возможны лишь процессы, сопровождающиеся увеличением энтропии (закон возрастания энтропии). В состоянии равновесия энтропия изолированной системыдостигает максимума и никакие макроскопич. процессы в такой системе невозможны.

второе начало термодинамики

ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ - один из осн. законов термодинамики, устанавливающий необратимость реальных термодинамич. процессов. В. н. т. сформулировано как закон природы H. Л. С. Карно (N. L. S. Carnot) в 1824, P. Клаузиусом (R. Clausius) в 1850 и У. Томсоном (Кельвином) (W. Thomson, Kelvin) в 1851 в различных, но эквивалентных формулировках. В. н. т. в формулировке Клаузиуса утверждает, что процесс, при к-ром не происходит никаких изменений, кроме передачи тепла от горячего тела к холодному, необратим, т. е. теплота не может самопроизвольно переходить от более холодного тела к более горячему (принцип Клаузиуса). Согласно формулировке Томсона, процесс, при к-ром работа переходит в тепло без к--л. иных изменений состояния системы, необратим, т. е. невозможно полностью преобразовать в работу всё тепло, взятое от тела, не производя никаких др. изменений состояния системы (принцип Tомсона). Принцип Томсона эквивалентен утверждению о невозможностивечного двигателя 2-го рода. В. н. т. можно сформулировать также в виде принципа Каратеодори: вблизи любого состояния термодинамич. равновесия и сколь угодно близко к нему существует состояние, в к-рое нельзя попасть при помощи адиабатич. процесса.

Из невозможности вечного двигателя 2-го рода следует Карно теорема о том, что кпд любого теплового двигателя не превосходит кпд Карно цикла  , к-рый определяется только темп-рой нагревателя T₁ и холодильника T₂. На основании теоремы Карно удаётся построить абс. шкалу темп-р (шкалу Кельвина, см. Абсолютная температура).

Рассматривая циклич. процесс, при к-ром система получает (или от неё отнимают) малые кол-ва теплоты dQ при абс. темп-ре T, можно сформулировать В. н. т. в виде Клаузиуса неравенства 

интеграл берётся по замкнутому циклу; если тепло отнимают, то считается, что   . Знак равенства относится к обратимым процессам (равенство Клаузиуса). Клаузиус установил неравенство (1), рассматривая циклич. процесс как предел суммы большого числа элементарных циклов Карно.

Из равенства Клаузиуса следует, что для равновесного процесса   есть полный дифференциал ф-ции состояния S, наз. энтропией. Если учесть первое начало термодинамики ,согласно к-рому

(U - внутр. энергия, P - давление, V - объём), то из В. н. т. следует, что существует интегрирующий множитель T^-1, к-рый делает выражение (2) полным дифференциалом   . Поэтому В. и. т. можно сформулировать в виде неравенства  . Неравенство Клаузиуса можно записать в след. виде:   (знак равенства соответствует обратимым процессам). Это неравенство - другая, интегральная формулировка В. н. т. Из него следует, что для адиабатически изолиров. системы  при необратимых процессах энтропия возрастает, а при обратимых - остаётся неизменной.

Др. эквивалентные формулировки В. н. т. можно получить с помощью любого термодинамического потенциала. Напр., дляГельмгольца энергии (свободной энергии)   получим .

При выборе в качестве термодинамич. потенциала Гиббса энергии  получим 

В кинетич. теории газов В. н. т. является следствием Болъцмана Н-теоремы, т. к. Н-функция Больцмана, определяемая через ср. логарифм ф-ции распределения атомов, пропорциональна энтропии идеального газа. Поэтому убывание энтропии имеет не абсолютный, а вероятностный характер.

В статистич. физике выясняется физ. смысл энтропии, связанной с логарифмом термодинамической вероятности Wсоотношением Больцмана  . Термодинамич. вероятность   определяется статистич. весом макроскопич. состояния. Возрастание энтропии означает переход системы из менее вероятного состояния в более вероятное.

В термодинамике неравновесных процессов В. н. т. оказывается следствием положительности производства энтропии (т. е. скорости её возрастания), к-рое является положительно определённой квадратичной формой от термодинамич. сил, характеризующих отклонение системы от состояния термодинамич. равновесия. T. о., неравновесная термодинамика даёт количественную характеристику В. н. т.

В статистич. физике устанавливают пределы применимости В. н. т., связанные с существованием флуктуации энтропии. Вывод о "тепловой смерти" Вселенной, к-рый иногда делают на основе применения к ней В. н. т. как к замкнутой термодинамич. системе, не является правомерным. Ошибочны также попытки опровергнуть этот вывод, учитывая возможность флуктуации, как это было сделано Л. Больцманом (L. Boltzmann). Дело в том, что в эволюции Вселенной существ. роль играет тяготение, к-рое не принималось во внимание.

Найдем полезную работу цикла Карно.

       Процесс А–В. Положительная работа, совершенная газом при изотермическом расширении одного моля газа от V₀ до V₁.

       Тепло, полученное от нагревателя Q₁, идет на изотермическое расширение газа, совершая при этом работу А₁:

.

(5.4.1)

Процесс В–С – адиабатическое расширение. При адиабатическом расширении теплообмен с окружающей средой отсутствует и работа расширения А₂ совершается за счет изменения внутренней энергии.

       Уравнение адиабаты:  .

       Давление при этом изменится до Р₂. Полученная работа на этой стадии:

.

(5.4.2)

       Процесс С–D – изотермическое сжатие. На третьем этапе газ изотермический сжимается V₂ до V₃. Теплота Q₂, отданная газом холодильнику при изотермическом сжатии, равна работе сжатия А₃ – это работа совершаемая над газом, она отрицательна:

.

(5.4.3)

       Процесс D–А – адиабатическое сжатие.

       Уравнение адиабаты:  . 

       Работа сжатия на последнем этапе:

(5.4.4)

       Общая работа цикла A = A₁ + A₂ + A₃ + A₄, или

.

       Обозначим  , тогда

(5.4.5)

       Значит работа, совершаемая газом больше работы внешних сил.

       Работа равна площади ограниченной кривой АВСDА.

       Из равенств следует:

.

(5.4.6)

       Полезная работа:

       КПД η равен:

(5.4.7)

      Из (5.4.7) видно, что η < 1, зависит от разности температур между нагревателем и холодильником (и не зависит от конструкции машины и рода рабочего тела). Это ещё одна формулировка теоремы Карно.

       Цикл Карно, рассмотренный нами, был на всех стади ях проведен так, что не было необратимых процессов (не было соприкосновения тел с разными температурами). Поэтому здесь самый большой КПД. Больше получить в принципе невозможно.

КПД η цикла Карно равен

η=T1−T2T1,

η = 0,40 = 40 %. КПД тепловой машины η можно найти и так:

η=AQn,(1)

где Q_n — количество теплоты, полученное газом от нагревателя,

A = Q_n – Q_x,   (2)

Q_x — количество теплоты, отдаваемое газом. Решим систему уравнений (1) и (2). Например,

Qn=Aη,Qx=Qn−A=A⋅(1η−1),

Q_x = 150 Дж.

24. Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева.

Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона:

где p — давление; V - объем T — температура; Z_r = Z_r (p,T)  — коэффициент сжимаемости газа; m - масса; М — молярная масса; R — газовая постоянная.

Свойства реальных газов

Реальные газы отличаются от идеальных газов тем, что молекулы этих газов имеют объемы и связаны между собой силами взаимодействия, которые уменьшаются с увеличением расстояния между молекулами. При практических расчетах различных свойств реальных газов наряду с уравнением состояния применяется отношение P·/(R·T)=c, которая называется коэффициентомсжимаемости.  Так как для идеальных газов при любых условиях P· = R·T, то для этих газов с = 1. Тогда величина коэффициента сжимаемостивыражает отклонение свойств реального газа от свойств идеального. Величина с для реальных газов в зависимости от давления итемпературы может принимать значения больше или меньше единицы и только при малых давлениях и высоких температурах она практически равна единице. Тогда реальные газы можно рассматривать как идеальные. В связи с отличием свойств реального газа от свойств идеального газа нужно иметь новые уравнения состояния, которые связывали бы значения P, х, T и давали бы возможность рассчитывать некоторые свойства газов для разных условий. Были предложены многочисленное число различных уравнений состояния реальных газов, но ни одно из них не решает проблему для общего случая. Развитие кинетической теории газов, позволило установит точное уравнение состояния реальных газов в виде:

P· = R·[1 -  /( + 1)·B_ / ^]. (6.1)

B_ – вириальные коэффициенты, выражаются через потенциальные энергию взаимодействия молекул данного газа и температуру Т. Однако это уравнение в общем виде не может быть использовано для непосредственных расчетов реальных газов. Для отдельных частных случаях получены расчетные уравнения того или иного реального газа. Из-за сложности вычисления вириальных коэффициентов обычно ограничиваются расчетом первых двух коэффициентов. Тогда расчетное уравнение имеет вид:

P· = R·(1 – А/ - B/ ²), (6.2)

где А и В - первый и второй вириальные коэффициенты, являющиеся функцией только температуры.  При расчете свойств многих реальных газов уравнения такого типа получили большое распространение.

25. Уравнение состояния

Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом итемпературой.

Для одного моля газа Ван-дер-Ваальса оно имеет вид:

где

•  — давление,

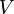•  — молярный объём,

•  — абсолютная температура,

•  — универсальная газовая постоянная.

Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка   учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка   — объем молекул газа.

Для   молей газа Ван-дер-Ваальса уравнение состояния выглядит так:

где

•  — объём,

[править]Вывод уравнения

Наиболее известны два способа получения уравнения: традиционный вывод самого Ван-дер-Ваальса и вывод методами статистической физики.

[править]Традиционный вывод

Рассмотрим сначала газ, в котором частицы не взаимодействуют друг с другом, такой газ удовлетворяет уравнению состояния идеального газа:

Далее предположим, что частицы данного газа являются упругими сферами одинакового радиуса r. Так как газ находится в сосуде конечного объёма, то пространство, где могут перемещаться частицы, будет несколько меньше. В исходной формуле следует вычесть из всего объёма некую его часть b, которая, вообще говоря, зависит только от вещества, из которого состоит газ. Таким образом, получается следующее уравнение:

Стоит заметить, что вычитаемый объём b не будет в точности равен суммарному объёму всех частиц. Если частицы считать твёрдыми и абсолютно упругими шариками, то вычитаемый объём будет примерно в четыре раза больше. Это легко объясняется тем, что центры упругих шаров не могут приближаться на расстояние ближе  .

Далее Ван-дер-Ваальс рассматривает силы притяжения между частицами газа и делает следующие допущения:

• Частицы распределёнными равномерно по всему объёму.

• Силы притяжения стенок сосуда не учитываются, что в общем случае неверно.

• Частицы, находящиеся внутри сосуда и непосредственно у стенок, ощущают притяжение по-разному: внутри сосуда действующие силы притяжения других частиц компенсируют друг друга.

Таким образом, для частиц внутри сосуда силы притяжения не учитываются. А частицы, находящиеся непосредственно у края сосуда, затягиваются внутрь силой, пропорциональной концентрации:

.

Число частиц, которые находятся непосредственно у стенок, в свою очередь тоже предполагается пропорциональным концентрации n. Можно считать, что давление на стенки сосуда меньше на некоторую величину, обратно пропорциональную квадрату объёма:

Окончательное уравнение: