Кпд. Тепловые двигатели

Коэффициент полезного действия  (КПД)  — это характеристика  результативности системы  в отношении  преобразования или передачи энергии,  который   определяется отношением  полезно использованной энергии к  суммарной  энергии, полученной системой.   КПД — величина  безразмерная, обычно  ее выражают  в процентах: Коэффициент полезного действия (КПД) теплового двигателя определяется по формуле: где A = Q1Q2. КПД  теплового двигателя  всегда меньше 1. Цикл Карно — это обратимый круговой  газовый процесс,  который состоит из последовательно стоящих  двух изотермических и двух адиабатных процессов, выполняемых с рабочим телом. 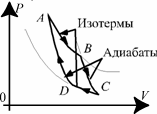Круговой цикл,  включающий в себя две изотермы и две адиа- баты, соответствует максимальному КПД. Французский инженер Сади  Карно в 1824 г.  вывел  формулу максимального КПД идеального теплового двигателя, где рабочее тело — это идеальный газ, цикл которого  состоял из двух изотерм и двух адиабат, т. е. цикл Карно. Цикл Карно — реальный рабочий цикл  теплового двигателя, свершающего работу за счет теплоты, подводимой рабочему телу в изотермическом процессе. Формула КПД цикла Карно, т. е. максимального КПД тепло- вого двигателя  имеет вид: где T1 — абсолютная температура нагревателя; Т2 — абсолютная температура холодильника. Тепловые двигатели — это  конструкции, в которых  тепловая энергия превращается в механическую. Тепловые двигатели  многообразны  как  по  конструкции, так и по  назначению.  К ним относятся паровые машины,  паровые турбины, двигатели внутреннего сгорания, реактивные двигатели.   Однако,  несмотря на многообразие, в принципе действия различ- ных тепловых двигателей  есть общие черты. Основные компонен- ты каждого теплового двигателя: 1)  нагреватель; 2)  рабочее тело; 3)  холодильник. Нагреватель выделяет тепловую  энергию,  при этом  нагревает рабочее тело, которое находится в рабочей камере двигателя. Рабочим телом может быть пар или газ. Приняв количество теплоты, газ расширяется, т.к.  его давление больше внешнего давления,  и двигает поршень, производя положительную работу. При этом его давление  падает, а объем увеличивается.  Если сжимать газ,  проходя те же состояния, но в обратном направлении, то совершим ту же по абсолютному значению,  но отрицательную работу. В итоге вся работа за цикл будет равна нулю. Для того чтобы работа теплового двигателя  была отлична от нуля, работа сжатия  газа должна быть меньше работы  расширения.  Чтобы  работа сжатия  стала меньше работы расширения, необходимо, чтобы процесс сжатия проходил при меньшей температуре, для этого рабочее тело нужно охладить, поэтому в конструкцию теплового двигателя  входит холодильник. Холодильнику рабочее тело отдает при соприкосновении с ним количество теплоты.

21. Энтропия идеального газа

Рассмотрим изменение энтропии идеального газа при изотермическом расширении его от объема V₁ до V₂.

Согласно формуле (2.38) совершаемая при этом механическая работа

.                                                          (2.63)

При изотермическом процессе работа равна теплу, переданному  или отданному системой A = ΔQ. По определению   и, стало быть, энтропия

.                                                  (2.64)

Это же выражение можно получить и непосредственно из определения (2.62). Пусть молекула газа находятся в объеме V. Вероятность нахождения одной молекулы в объеме V пропорциональна объему V. Вероятность нахождения N молекул в этом же объеме пропорциональна V^N, поскольку эта вероятность представляет собой вероятность N независимых событий. Таким образом, изменение энтропии при расширении газа есть

,

что аналогично формуле (2.64).

Энтропия системы является функцией ее состояния, определенная с точностью до произвольной постоянной.         Если система совершает равновесный переход из состояния 1 в состояние 2, то изменение энтропии

.

(6.2.1)

       Таким образом, по формуле (6.2.1) можно определить энтропию лишь с точностью до аддитивной постоянной, т.е. начало энтропии произвольно. Физический смысл имеет лишь разность энтропий.         Исходя из этого, найдем изменения энтропии в процессах идеального газа.         Так как при Т = const,

,

,

, или

.

(6.2.2)

Таким образом, изменение энтропии ΔS_1-2 идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида перехода 1 - 2.         Каждый из изопроцессов идеального газа характеризуется своим изменением энтропии, а именно:

• изохорический: 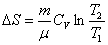  , т.к.  ;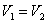

• изобарический: 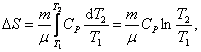  т.к. Р₁ = Р₂;

• изотермический: 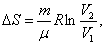  т.к.  ;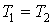

• адиабатический: 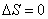  , т.к.