«22»Производная функции. Задачи ,приводящие к понятию производной.

Производной функции f(x) в точке х называется предел отношения приращения функции в точке х к приращению аргумента, когда приращение аргумента стремится к нулю, если этот предел существует

Задачи

Рассмотрим на примере Х^(2)

1. Фиксируем Х ; y(x)=x-∆x

2. Задаем приращение Х-∆Х

3. Составим разность ∆У=У(Х-∆Х)-У(Х)=(Х+∆Х)^(2)- X^(2)= ∆Х(2Х-∆Х)

4. Составим отошени разность ∆У : ∆Х= ∆Х(2Х+ ∆Х) : ∆Х=2Х+ ∆Х

5. Вычислить предел y’=LIM ∆y = ∆x(2X+∆x)= 2x+∆x (там деление)

∆x->∞ ∆X ∆x (полоски нет)

«23»Физический и геометрический смысл производной.

Определение

Функция y = f(x), имеющая производную в каждой точке интервала (a, b), называется дифференцируемой в этом интервале;операция нахождения производной функции называется дифференцированием.

В задаче про скорость прямолинейного движения было получено V = lim ∆s/∆t.

∆t→

. Это равенство перепишем в виде V = ′, т. е. скорость прямолинейного движения материальной точки в момент времени t -это производная от пути S по времени t. В этом заключается механический смысл производной.

Обобщая, можно сказать, что если функция y = f(x) описывает какой - либо физический процесс, то производная y’- это скорость протекания этого процесса. В этом состоит физический смысл производной.

В задаче про касательную к кривой был найден угловой коэффициент касательной

k = tg α = lim ∆Y/∆X. Это равенство перепишем в виде f′(x) = tg α = k, т.е. производная f′(x) в точке ∆x→0 x равна угловому коэффициенту касательной к графику функции y = f(x) . в точке, абсцисса которой равна x. В этом заключается геометрический . . . смысл производной.

«24»Вычисление производной на основе ее определения.

Определение производной

Рассмотрим функцию f(x), область определения которой содержит некоторый открытый интервал вокруг точки x0. Тогда функция f(x) является дифференцируемой в точке x0, ее производная определяется формулой Для производной используются обозначения:

Для нахождения производной функции f(x) в точке x0 на основе определения следует выполнить следующие действия: Записать отношение  Упростить дробь, сократив ее, если возможно, на Δx; Найти производную  , вычисляя предел дроби. Если данный предел существует, то говорят, что функция  f(x) дифференцируема в точке x = x0.  Пример 1 Используя определение, найти производную функции  Решение. По определению производной «25»Непрерывность диффиренцируемой функции. Теорема 1. Пусть функция y = f(x) дифференцируема на интервале (a, b). Тогда функция f непрерывна на (a, b). Доказательство Возьмем произвольное фиксированное число x   (a,b). По условию теоремы Следовательно, в малой окрестности числа x0 можно определить функцию α = α(Δx), стремящуюся к нулю при   такую, что Но тогда и следовательно, функция f непрерывна при x = x0. Так как число x0 – произвольное, то функция fнепрерывна на всем интервале (a, b). «26» Производная суммы, разности, произведения и частного двух функций. суммы (разности) произведения частного 2-х фунций

«27»Производная сложной функции

Сложная функция – это функция, аргументом которой также является функция.

С нашей точки зрения, это определение наиболее понятно. Условно можно обозначать какf(g(x)). То есть, g(x) как бы аргумент функции f(g(x)).

К примеру, пусть f – функция арктангенса, а g(x) = lnx есть функция натурального логарифма, тогда сложная функция f(g(x)) представляет собой arctg(lnx). Еще пример: f – функция возведения в четвертую степень,

а - целая рациональная функция (смотритеклассифика- цию элементарных функций), тогда

«28»Производная обратной и параметрически заданной функции.

Производная обратной функции

Дифференцируемая монотонная функция f: ]a, b[ → R с необращающейся в нуль производной имеет обратную дифференцируемую функцию f^-1, производная которой вычисляется по формуле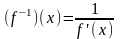

Производная параметрически заданной функции

Если функция f задана параметрически

x = φ(t), y = ψ(t), α < t < β,

где y = f(x) и функции φ и ψ дифференцируемы, причем φ'(t) ≠ 0, то

«29»Производная и

и

«30»Производные и

и

«31»Производный y= arcsinX и y=arcos X

и

«32»Производные y=arctg X и y =arcctg X

и

«33»Производная 2-го порядка и ее физический смысл

Если функция f’ дифференцируема, то ее производную называют второй производной от f и обозначают f”: f” = (f’)’

Вторая производная от параметрической функции x = x (t) и y = y (t) задается формулой:

Физический смысл производной второго порядка проясняется из того, что если первая производная f’(x) задаёт мгновенную скорость изменения значений f(x) в момент времениx в момент времени f’(x), задаёт мгновенную скорость изменения значений мгновенной скорости, то есть ускорение значений f(x).

Следовательно, третья производная - это скорость изменения ускорения (или, что то же самое, ускорение изменения скорости, поскольку, как очевидно следует из определения,

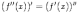
«34»Правило лопиталя

Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность  типа 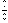  или  .  Пусть a является некоторым конечным действительным числом или равно бесконечности.

Если  и ,то

Если и ,то аналогично

Правило Лопиталя можно также применять к неопределенностям типа  . Первые две неопределенности   можно свести к типу   или   с помощью алгебраических преобразований. А неопределенности 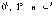  сводятся к типу   с помощью соотношения

Правило Лопиталя справедливо также и для односторонних пределов

ПРИМЕР 1 .

Решение.

Поскольку прямая подстановка приводит к неопределенности типа  , применяем правило Лопиталя

Пример 2   .

 Решение.

Используя правило Лопиталя, можно записать

«35»Интервалы монотонности функции. Необходимые условия.

Функция называется возрастающей если Х1>X2f(x1)>f(x2)

Функция называется убывающей если Х1>X2f(x1)<f(x2)

Если функция только возрастающая или только убывающая ,то она называется МОНОТОННОЙ.

ТЕОРЕМА 1(НЕОБХОДИМЫЕ УСЛОВИЯ)

ЕСЛИ ФУНКЦИЯ f(x) ДИФФЕРЕНЦИМА И ВОЗРАСТАЕТ (УБЫВАЕТ) НА ИНТЕРВАЛЕ (a,b),

ТО f’(x) 0 ( f’(x) 0) ДЛЯ ЛЮБОЙ Х ПРИНАДЛЕЖАЩЕЙ (a,b).

ДОКАЗАТЕЛЬСТВО

Хо-произвольная точка из (а,b)

Рассмотрим случай возрастания

Для Х>Хо f(X) f(Xo)

Для Х<Хо f(X) f(Xo)

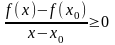 , так как функция дифференцима

= .

«36»Теорема Ролля

Пусть:

1. Функция   непрерывна на отрезке  :  ;

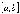2. Для любого x из интервала   существует производная:  ;

3. на концах отрезка [a, b] принимает равные значения.

Доказательство

1. Функция непрерывна   существуют  .

2. Если  , то функция   является константой, и ее производная в любой точке равна 0, т.е. теорема доказана.

3. Если же  , то оба значения   не могут достигаться в концевых точках, т.к. 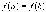  и  . Тогда хотя бы одно из них достигается во внутренней точке c, и, по теореме Ферма    

Замечания:

1. Существует хотя бы одна точка, в которой касательная к графику функции параллельна оси Ox (см. рисунок к теореме Ферма).

2. Все условия теоремы Ролля существенны, т.е. нельзя отбростиь хотя бы одно из них.

«37»Теорема Лагранжа

Пусть:  1) f(x) определена и непрерывна в замкнутом промежутке [а,b],  2) существует конечная производная f/(x) , по крайней мере, в открытом промежутке (а,b). Тогда между aи b найдется такая точка с(a< с <b), что для нее выполняется равенство

Доказательство. Введем вспомогательную функцию, определив ее в промежутке [а,b] равенством: F(x)=f(x)−f(a)− (x−a).

Эта функция удовлетворяет всем условиям теоремы Ролля. В самом деле, она непрерывна в [а,b], так как представляет собой разность между непрерывной функцией f(x) и линейной функцией. В промежутке (а,b)она имеет определенную конечную производную, равную F/(x)=f/(x)−

Наконец, непосредственной подстановкой убеждаемся в том, чтоF(a)=F(b)= 0, т. е. F(x) принимает равные значения на концах  промежутка.

Следовательно, к функции F(x) можно применить теорему Ролля и утверждать существование в (а,b)такой точки с, что F′(с)=0. Таким образом, f ‘ (c)− =0

Откуда =f ‘(c) Теорема Доказана.

Геометрическая смысл теоремы Лагранжа. Обращаясь к геометрическому истолкованию теоремы Лагранжа, заметим, что отношение =

есть угловой коэффициент секущей АВ, а f/(c) есть угловой коэффициент касательной к кривой y=f(x) в точке с абсциссой x=c. Таким образом, утверждение теоремы Лагранжа равносильно следующему: на дуге АВ всегда найдется, по крайней мере, одна точка М, в которой касательная параллельна хорде АВ.

«38»Достаточные условия монотонности функции

Достаточное условие строгой монотонности функции на промежутке.

Теорема (достаточное условие) Если функция f(x) дифференцируема на (a,b) и f/(x)≥0  (f/(x)≤0)  на (a,b), то f(x) не убывает (не возрастает) на (a,b). Доказательство Рассмотрим случай когда f/(x)≥0 . Рассмотрим две точки x1,x2∈(a,b)  и применим формулу Лагранжа. На [x1,x2] функция f(x) удовлетворяет всем условиям этой теоремы. Следует, чтоx1<x2: f(x2)−f(x1)=f/(c)(x2−x1),  где c∈(x1,x2)  и правая часть больше нуля, значит f(x2)−f(x1)≥0  или f(x2)≥f(x1)  при x2>x1, функция не убывает. Теорема доказана. Замечание Если требовать, что f/(x)>0  (f/(x)<0) , тогда функция строго возрастает (убывает).

 

«39» Экстремумы. Т.Ферма

Необходимые условия экстремума. Если точка x_о является точкой экстремума функции f(x), то либо f ^'(x_о) = 0, либо f (x_о) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть x_о - критическая точка. Если f ^' (x) при переходе через точку x_о меняет знак плюс на минус, то в точке x_о функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x_о экстремума нет.

Второе достаточное условие. Пусть функция f(x) имеет производную  f ^' (x) в окрестности точки x_о и вторую производную   в самой точке x_о. Если f ^' (x_о) = 0,  >0 ( <0), то точка x_оявляется точкой локального минимума (максимума) функции f(x). Если же  =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].

Пример 3.22. Найти экстремумы функции f(x) = 2x³ - 15x²+ 36x - 14.

Решение. Так как f ^'(x) = 6x² - 30x +36 = 6(x -2)(x - 3), то критические точки функции x₁ = 2 и x₂ = 3. Экстремумы могут быть только в этих точках. Так как при переходе через точку x₁ = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку x₂ = 3 производная меняет знак минус на плюс, поэтому в точке x₂ = 3 у функции минимум. Вычислив значения функции в точках x₁ = 2 и x₂ = 3, найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) = 13.

Теорема Ферма

Если функция   имеет производную и в точке   имеет экстремум, то значение производной в этой точке равно 0.

Доказательство

Пусть   - точка минимума. Тогда при 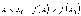 . Значение выражения  . Значит,  . Рассмотрим теперь  , при этом также  , и выражение  . Значит, правая производная  . По теореме 14.5  . Из ранее доказанного следует:  . Теорема доказана.

«40»Достаточные условия экстремума

По теореме Ферма достаточное условие экстремума f'(x₀)=0. Значит, для того чтобы найти точки «подозрительные» на экстремум, нужно взять производную от функции f(x₀), приравнять ее к нулю и решить получившееся уравнение. Однако, не все корни этого уравнения будут экстремумами. Для того чтобы выяснить наверняка, является ли точка точкой экстремума, нужно знать достаточное условие экстремума. Корни уравнения f'(x₀)=0 называют стационарными точками. Достаточное условие экстремума: Если при переходе через стационарную точку производная меняет знак, то эта точка является экстремумом. Если меняет знак с «+» на «-», то это точка максимума. Если меняет знак с «-» на «+», то это точка минимума. Если при переходе через стационарную точку производная не меняет знак, то эта точка не является экстремумом. Очевидно, что точки, в которых функция принимает максимальное значение на некотором промежутке нужно искать среди точек максимума. А точки, в которых функция принимает минимальное значение - среди точек минимума. Однако нельзя забывать, что максимальное (минимальное) значение функция может принимать и на концах промежутка.

«41»Выпуклость графика. Достаточные условия.

ОПРЕДЕЛЕНИЕ. Кривая y = f(x) называется выпуклой (вогнутой) на интервале (a;b) если x(a;b) кривая выпукла (вогнута) в соответствующей точке M(x ; f(x)). Замечания.

1)Если M₀(x₀ ; f(x₀)) – точка перегиба кривой y = f(x), то x₀ – внутренняя точка области определения функции f(x).

2) Точками перегиба кривой y = f(x) часто называют точки, которые разделяют интервалы выпуклости и вогнутости этой кривой (т.е. абсциссы точек перегиба кривой y = f(x)).

Достаточное условие вогнутости ( выпуклости ) функции.

Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:

если  f '' ( x ) > 0 для любого x   ( a, b ), то функция  f ( x ) является вогнутой на интервале ( a, b );

если  f '' ( x ) < 0 для любого x   ( a, b ), то функция  f ( x ) является выпуклой на интервале ( a, b ) .

 Замечание. Точки, в которых вторая производная функции y = f(x) обращается в ноль или имеет разрыв, называют иногда критическими точками II рода функции y = f(x) (или критическими точками функции y = f(x) по второй производной).

«42»Асимптоты графика

Определение. Асимптотой графика функции y=f(x) называется прямая, обладающая тем свойством, что расстояние от точки(x ,f(x))   графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.

По способам их отыскания выделяют три вида асимптот: вертикальные x=a , горизонтальные y=b  , наклонные y=kx+b

Очевидно, горизонтальные являются частными случаями наклонных (приk=0).

Нахождение асимптот графика функции основано на следующих утверждениях.

Теорема 1. Пусть функция   определена хотя бы в некоторой полуокрестности точки   и хотя бы один из ее односторонних пределов в этой точке бесконечен, т.е. равен   или  . Тогда прямая   является вертикальной асимптотой графика функции.

Таким образом,  вертикальные асимптоты графика функции следует искать в точках разрыва функции или на концах ее области определения (если это конечные числа).

Теорема 2. Пусть функция   определена при значениях аргумента, достаточно больших по абсолютной величине, и существует конечный предел функции  . Тогда прямая   есть горизонтальная асимптота графика функции  .

Может случиться, что  , а  , причем   и   - конечные числа, тогда график имеет две различные горизонтальные асимптоты: левостороннюю и правостороннюю. Если же существует лишь один из конечных пределов   или  , то график имеет либо одну левостороннюю, либо одну правостороннюю горизонтальную асимптоту.

Теорема 3. Пусть функция   определена при значениях аргумента, достаточно больших по абсолютной величине, и существуют конечные пределы    и  . Тогда прямая   является наклонной асимптотой графика функции  .

Заметим, что если хотя бы один из указанных пределов бесконечен, то наклонной асимптоты нет.

Наклонная асимптота так же, как и горизонтальная, может быть односторонней.

«43»Дифференциал функции. Геометрический смысл дифференциала

 Понятие дифференциала функции

Пусть функция у=ƒ(х) имеет в точке х отличную от нуля производную.

Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать D у/Dх=ƒ'(х)+α, где α→0 при ∆х→0, или ∆у=ƒ'(х)•∆х+α•∆х.

Таким образом, приращение функции ∆у представляет собой сумму двух слагаемых ƒ'(х)•∆х и а•∆х, являющихся бесконечно малыми при ∆x→0. При этом первое слагаемое есть бесконечно малая функция одного порядка с ∆х, так как а второе слагаемое есть бесконечно малая функция более высокого порядка, чем ∆х:

Поэтому первое слагаемое ƒ'(х)· ∆х называют главной частью приращения функции ∆у.

Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):

dy=ƒ'(х)•∆х.                                        (24.1)

Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х. Так как у'=х'=1, то, согласно формуле (24.1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.

Поэтому формулу (24.1) можно записать так:

dy=ƒ'(х)dх,                                              (24.2)

иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной .Из формулы (24.2) следует равенство dy/dx=ƒ'(х). Теперь обозначение производной dy/dx можно рассматривать как отношение дифференциалов dy и dх.

Геометрический смысл дифференциала функции

Выясним геометрический смысл дифференциала.

Для этого проведем к графику функции у=ƒ(х) в точке М(х; у) касательную МТ и рассмотрим ординату этой касательной для точки х+∆х (см. рис. 138). На рисунке ½ АМ½ =∆х, |AM₁|=∆у. Из прямоугольного треугольника МАВ имеем:

Но, согласно геометрическому смыслу производной, tga=ƒ'(х). Поэтому АВ=ƒ'(х)•∆х.

Сравнивая полученный результат с формулой (24.1), получаем dy=АВ, т. е. дифференциал функции у=ƒ(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.

В этом и состоит геометрический смысл дифференциала.

«44»Кривизна кривой (правильность билета под ?)

Вычисление кривизны кривой

Р ассмотрим кривую L, задаваемую дифференцируемой функцией y = f(x) (см. рис. 12). На кривой возьмем фиксированную точку P₀(x₀, y₀), где y₀ = f(x₀), и подвижную точку P(x, y). Пусть функция s = s(x)описывает длину дуги  . Зададим x приращение Δx. Это вызовет изменение длины дуги на Δs, где  . Далее, через точки P, P₁ проведем касательные. Пусть угол между касательной к точке P и осью Ox равен α, а угол между касательной к точке P₁ и осью Ox равен α + Δα. Тогда угол между касательными равен Δα.

Определение 11. Кривизной K кривой в точке Pназывается предел отношения   при стремленииΔs к нулю, т.е. 

Кривизна K является одной из важнейших характеристик кривой и выражает степень искривленности кривой.

Выведем формулу для вычисления кривизны кривой в каждой ее точке. Из определения производной следует, что  . Следовательно,  . Далее выполним преобразования 

Для того, чтобы найти K, необходимо определить производные α'(x), s'(x). Производнаяs'(x) задается формулой (9). Для нахождения производной α'(x) сначала заметим, что tg α = y'(см. п. 1.2), следовательно, α = arctg y'. Дифференцируя это равенство, получаем

Так как  , то формула для вычисления кривизны кривой имеет вид

«45»Функция многих переменных. Задачи, приводящие к функции многих переменных и определение.

«46» Предел и непрерывность функций двух переменных

Пусть функция Z=f(M) определена на некотором множестве {M} и точка M₀ {M} или M₀ {M}, но обладает тем свойством, что в любой δ-окрестности этой точки содержится хотя бы одна точка множества {M}, отличная от M₀.

ОПРЕДЕЛЕНИЕ 1: Число А называется пределом функции Z=f(M) в точке M₀, если функция Z=f(M) определена в окрестности точки M₀ и для любого ε>0, δ>0 такое что при |M₀M|<δ, выполняется неравенство |f(M)-A|<ε.

обозначение: 

ОПРЕДЕЛЕНИЕ 2: Функция Z=f(M) называется непрерывной в точке M₀, если предел функции в этой точке существует и равен значению функции в этой точке, т.е.