Сложение матриц и их свойства.

Пусть n и m — фиксированные натуральные числа. Рассмотрим множество матриц над некоторым числовым полем Р размером n x m, обозначим его Р_{n x m} .

Определение 5. Возьмем две матрицы A, B Р_{n x m.} Под суммой матриц A и B (обозначают А+В) понимают матрицу С  Р_{n x m} такую, что c_ij =a_ij + b_ij. для всех i=1,…,n; j=1,…,m.,т.е. чтобы сложить две матрицы, надо сложить элементы, стоящие на одинаковых местах.

Свойство 1. Сложение матриц ассоциативно, т.е. (А+В)+С = А + (В+С) и коммутативно, т.е. А+В=В+А, .

 Доказательство следует из соответствующих свойств для чисел. 

Свойство 2. Если нулевую матрицу прибавить к произвольной матрице тех же размеров, то последняя не изменится.

Свойство 3. Для любой матрицы A  Р_{n x m}  B  Р_{n x m} такая, что А+В=0. Такая матрица В называется противоположной к матрице А.

Умножение матрицы на число и его свойства.

Определение 6. Пусть А  Р_{n x m} ,   Р — произвольный элемент поля Р. Под произведением А понимают матрицу В тех же размеров такую, что b_ij =  a_ij.

Свойство 1. 1А = А .

Свойство 2. (+) А = А + А. (Умножение матрицы на число дистрибутивно относительно сложения чисел) .

Свойство 3.  (А + В) = А + В. (Умножение числа на сумму матриц дистрибутивно относительно сложения матриц) .

Свойство 4. () А =  (А) .

 Доказательство проводится сравнением элементов матриц левой и правой частей равенства. Например, рассмотрим свойство 2. Известно, что (+)a_ij =  a_ij +  a_ij, где a_ij — произвольный элемент матрицы А,(дистрибутивность умножения относительно сложения элементов поля). 

§2. Умножение матриц.

Мы никак не мотивировали операцию сложения матриц, но едва ли это вызвало недоумение в силу своей естественности. Операция умножения матриц уже не обладает этим качеством.

Пусть A = (a_ij)_{m x n} , B = (b_ij)_{n x p}. Под произведением АВ понимают

матрицу С с элементами c_ij = .

АВ := С= (с_ij)_{m x p}.

Например, А = и В = .

Тогда AВ =

5=1 0 + 2 1 + 3 1

6=1 1 + 2 1 + 3 1

7= 1 4 + 2 0 + 3 1 и т.д.

Берется i-тая строка матрицы А и j-тый столбец матрицы В, перемножаются покомпонентно и результаты складываются. Это есть элемент матрицы С на позиции i,j.

Свойство. Произведение матриц не коммутативно, т.е. АВ ВА, в том числе и квадратных.

Пример (доказывающий свойство):

=

=

Замечание 1. Запись A = (a_ij)_{m x n} обозначает, что матрица А имеет размеры

m x n.

Замечание 2. В двойной сумме результат суммирования не зависит от порядка суммирования, т.е.

, ибо левая часть равенства и правая часть есть сумма элементов матрицы .

Теорема (об ассоциативности произведения матриц).

Пусть А, В, С — матрицы над числовым полем Р такие, что определено произведение АВ и ВС. Тогда имеют смысл произведения (АВ)С, А(ВС) и верно равенство (АВ)С = А(ВС).

 Пусть A = (a_ij)_{m x n} , B = (b_ij)_{n x p} , С = (с_ij)_{р x s} . Они подходящих размеров, чтобы было определено и . Введем обозначения АВ = (d_ij)_{m x p} , BC = (l_ij)_{n x s} , A(BC) = (f_ij)_{m x s} , (AB)C = (r_ij)_{m x s} . Матрицы A(BC) и (AB)C одинаковых размеров. Требуется проверить, что f_ij = r_ij . Выразим f_ij и r_ij через элементы матриц А, В, С:

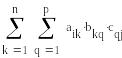
f_ij = = = . _,

.

Полученные суммы отличаются лишь порядком суммирования, что не влияет на результат (по замечанию 2). 

Определение. Произведение нескольких матриц определим индуктивно, т.е. если имеем k матриц, то их произведение определим следующим образом: (A₁, ... , A_k-1) A_k

Упражнение. Доказать, что в произведении нескольких матриц скобки можно расставлять как угодно.

Указание. Воспользоваться ассоциативностью.

Теорема 2. Пусть A = (a_ij)_{m x n} . Тогда AE_n = E_mA = A, где Е — единичная матрица подходящего размера.

 Доказательство проводится непосредственной проверкой равенства:

=

Аналогично доказывается, что E_mA = А .

Теорема 3. Пусть A = (a_ij)_{m x n} . Тогда АО_{n x s} = O_{m x s} , где О — нулевая матрица подходящего размера.

 Произведение таких матриц будет матрицей размером m x s. Каждый элемент, очевидно, будет равен 0. 

Теорема 4 (дистрибутивность умножения матриц относительно сложения матриц).

(А + В)С = АС + ВС, где С — матрица подходящего размера, и — матрицы одинаковых размеров.

 Пусть A = (a_ij)_{m x n} , B = (b_ij)_{m x n} , С = (с_ij)_{n x p} . Понятно, что (А + В)С и АС + ВС одинаковых размеров. Чтобы доказать их равенство, надо показать, что на одних и тех же местах стоят одни и те же элементы.

Следующее равенство доказывает теорему:

элемент на элемент элемент на

позиции на позиции позиции

матрицы матрицы матрицы



Транспонирование матриц.

Определение 1. Пусть A = (a_ij)_{m x n} . Транспонирование матрицы — это такое ее преобразование, при котором строка с номером i записывается в столбец с тем же номером.

Обозначение: А^t , А^tr , А'.

Пример:

, то .

Теорема 5. Имеют место следующие равенства:

1. (А^t)^t = A.

2. (αA + βB)^t = αA^t + βB^t.

3. (AB)^t = В^tА^t .

Причем, А и В — матрицы подходящих размеров, α и β — любые числа.

 1. А = (а_ij)_{m x n}

(A)^t = (а_ji)_{n x m} (А^t)^t = A.

2. Доказать самостоятельно.

3. Пусть имеем А = (а_ij)_{m x n} и B = (b_ij)_{n x s} . Тогда A^t = ( _ij)_{n x m} , B^t = =( _ij)_{s x n}, AB = (c_ij)_{m x s}, B^tА^t = (d_ij)_{s x m} , (AB)^t = ( _ij)_{s x m}.

Матрица В^tA^t и (AB)^t одинаковых размеров, и чтобы доказать, что В^tA^t = (AB)^t , надо показать, что на одинаковых местах стоят одинаковые элементы.

.

Мы получили, что на позиции ij у матрицы В^tA^t и матрицы (AB)^t стоит один и тот же элемент. 

Определение 2. Матрица А называется симметрической, если А^t = А, и кососимметрической, если А^t = -А.

Пример. Симметрическая матрица:

кососимметрическая матрица:

Упражнение. Будет ли произведение симметрических (кососимметрических) матриц симметрической (кососимметрической) матрицей? Если будет, доказать. Если не будет, привести пример.