
- •41 Теория подобия центробежных насосов
- •Регулирование подачи центробежных насосов
- •46 Классификация насосов
- •Насосы возвратно-поступательного действия
- •48 Шестеренчатые насосы Принцип действия шестеренчатых насосов
- •Функции гидропривода
- •Виды гидроприводов
- •Гидропривод с разомкнутой системой циркуляции
- •52 Определение кпд гидропривода при постоянной нагрузке
- •5.2 Определение кпд гидропривода при работе в цикличном режиме
- •Устройство и принцип действия
- •55 Водоструйные установки и водоподъемники
- •57 Водокольцевой насос
- •Принцип работы и особенности
1. Предмет гидравлики: Гидравлика — прикладная наука о законах движения (капельных жидкостей и газов) и равновесии жидкостей (гидростатика) и способах приложения этих законов к решению задач инженерной практики. В отличие от гидромеханики, гидравлика характеризуется особым подходом к изучению явлений течения жидкостей; она устанавливает приближённые зависимости, ограничиваясь во многих случаях рассмотрением одноразмерного движения, широко используя при этом эксперимент, как в лабораторных, так и в натурных условиях. Наряду с этим намечается всё большее сближение между гидромеханикой и гидравликой: с одной стороны, гидромеханика всё чаще обращается к эксперименту, с другой — методы гидравлического анализа становятся более строгими. Гидравлика широко использует теоретические положения механики и данные экспериментов. В прошлом гидравлика носила чисто экспериментальный и прикладной характер, в последнее время её теоретические основы получили значительное развитие, это способствовало сближению её с гидромеханикой. Гидравлика решает многочисленные инженерные задачи, рассматривает многие вопросы гидрологии, в частности, законы движения речных потоков, перемещения ими наносов, льда и шуги, процессы формирования русла и т. д. Этот комплекс вопросов объединяется речной гидравликой (динамикой русловых потоков), которую можно рассматривать как самостоятельный раздел гидравлики. По отношению к гидромеханике гидравлика выступает как инженерное направление, получающее решение многих задач о движении жидкости на основе сочетания эмпирических зависимостей, установленных опытным путём, с теоретическими выводами гидромеханики. В гидравлике рассматриваются также движение наносов в открытых потоках и пульпы в трубах, методы гидравлических измерений, моделирование гидравлических явлений и некоторые др. вопросы. Существенно важные для расчёта гидротехнических сооружений вопросы гидравлики — неравномерное и неустановившееся движение в открытых руслах и трубах, течение с переменным расходом, фильтрация и др. — иногда объединяют под общим названием «инженерная гидравлика», или «гидравлика сооружений». Таким образом, круг вопросов, охватываемых гидравликой, весьма обширен, и ее законы в той или иной мере находят применение практически во всех областях инженерной деятельности, особенно в гидротехнике, мелиорации, водоснабжении, канализации, теплогазоснабжении, гидромеханизации, гидроэнергетике, водном транспорте и др.
2. Понятие о жидкости: Жидкостью называется вещество (промежуточное между твердым и газообразным), находящееся в конденсированном агрегатном состоянии и обладающее способностью легко изменять свою форму под действием весьма незначительных сил. Жидкости подобно твердым телам, обладают малой сжимаемостью и большой плотностью, но в то же время, подобно газам, не обладают упругостью формы. Наиболее характерным свойством жидкости является текучесть.
Континуум считается непрерывной средой без пустот и промежутков, свойства которой одинаковы во всех направлениях. Это означает, что все характеристики жидкости являются непрерывными функциями и все частные производные по всем переменным также непрерывны.
Реальная жидкость не допускает наличия разрывов непрерывности ни внутри движущегося потока, ни на границах его с твердым телом. В действительности жидкость или газ не могут скользить вдоль поверхности твердого тела; скорости тех частиц, которые граничат с твердой стенкой, равны нулю, жидкость как бы прилипает к поверхности тела. Однако эта скорость резко возрастает при удалении от поверхности и на внешней границе весьма тонкого по сравнению с размерами тела пограничного слоя достигает значений, соответствующих схеме свободного скольжения идеальной жидкости. В случае плохо обтекаемого тела пограничный слой отрывается от поверхности тела и значительно искажает картину обтекания тела идеальной жидкостью. Подробнее об этом будет сказано в главе VIII, посвященной динамике вязкой жидкости. Реальные жидкости не являются абсолютно подвижными. Реальные жидкости обладают рядом физических свойств, которые во многом определяют область их использования. Для изучения курса гидравлики из физических свойств жидкостей наиболее важными являются плотность (весомость), удельный объем, температурное расширение, сжимаемость, вязкость.
Идеальная жидкость — в гидродинамике — воображаемая (идеализированная) жидкость, в которой, в отличие от реальной жидкости, отсутствует вязкость. В идеальной жидкости отсутствует внутреннее трение, то есть, нет касательных напряжений между двумя соседними слоями. Моделью идеальной жидкости пользуются при теоретическом рассмотрении задач, в которых вязкость не является определяющим фактором и ею можно пренебречь. В частности, такая идеализация допустима во многих случаях течения, рассматриваемых гидроаэромеханикой, и даёт хорошее описание реальных течений жидкостей и газов на достаточном удалении от омываемых твёрдых поверхностей и поверхностей раздела с неподвижной средой. Математическое описание течений идеальных жидкостей позволяет найти теоретическое решение ряда задач о движении жидкостей и газов в каналах различной формы, при истечении струй и при обтекании тел.
3. Силы, действующие в жидкости: Внешние силы могут быть поверхностными и объемными (массовыми). Поверхностные силы - это силы, действующие непосредственно на граничную (внешнюю) поверхность выделенного объема жидкости и пропорциональны площади этой поверхности. Они обусловлены воздействием соседних объемов жидкости на данный объем или воздействием других тел. Объемные (массовые) силы пропорциональны массе выделенного объема жидкости (или при постоянной плотности среды пропорциональны объему) и действуют на все частицы среды этого объема. Примером объемных сил являются сила тяжести, центробежная сила, сила инерции и др.
4. Физические свойства жидкости:
1) Основной механической характеристикой жидкости является плотность , определяемая для однородной жидкости отношением ее массы m к занимаемому объему , кг/м3. Плотность однородной жидкости одинакова во всех точках. Для определения плотности служат ареометры.
2) Вес жидкости, приходящийся на единицу объема, называется удельным весом γ, Н/м3 и определяется по формуле
![]() Где G
- вес жидкости в объеме V.
Где G
- вес жидкости в объеме V.
Удельный вес - величина размерная и измеряется в системе СИ в ньютонах на кубический метр - Н/м3.
3) Температурное расширение - способность жидкостей изменять объем при изменении температуры. Для капельных жидкостей характеризуется коэффициентом температурного расширения βt, равным относительному изменению объема при изменении температуры t на один градус при постоянном давлении:
![]() где
W
- первоначальный объем; ∆W
- изменение этого объема при повышении
температуры на величину ∆t
Коэффициент температурного расширения
в системе СИ имеет размерность град-1.
где
W
- первоначальный объем; ∆W
- изменение этого объема при повышении
температуры на величину ∆t
Коэффициент температурного расширения
в системе СИ имеет размерность град-1.
Коэффициент βt зависит для данной жидкости от температуры и давления.
4) Сжимаемость - способность жидкостей уменьшать объем при увеличении давления. Характеризуется коэффициентом объемного сжатия βw , который представляет собой относительное изменение объема жидкости на единицу изменения давления:
![]() где
W
- первоначальный объем жидкости; ∆W
- приращение (изменение) этого объема
при увеличении давления на величину ∆p
.
где
W
- первоначальный объем жидкости; ∆W
- приращение (изменение) этого объема
при увеличении давления на величину ∆p
.
Коэффициент объемного сжатия в системе СИ имеет размерность Па-1. Знак минус в этой формуле обусловлен тем, что положительному приращению давления p соответствует отрицательное приращение (т.е. уменьшение) объема жидкости.
Процесс изменения объема V жидкости под влиянием давления может происходить в различных условиях: изотермически при t = const и адиабатически. Сжатие жидкости можно считать изотермическим, если процесс происходит медленно и выделяющееся тепло успевает рассеиваться. При быстро протекающем объемном сжатии процесс нужно считать адиабатическим. В соответствии с этим различают изотермический и адиабатический коэффициенты объемного сжатия. Величина этих коэффициентов зависит от температуры и давления. Величина, обратная коэффициенту объемного сжатия, называется соответственно изотермическим и адиабатическим модулем упругости:
![]() Модуль
упругости Е большинства жидкостей
настолько велик, что жидкости можно
считать практически несжимаемыми.
Иногда сжимаемость жидкостей полезна
- ее используют в гидравлических
амортизаторах и пружинах.
Модуль
упругости Е большинства жидкостей
настолько велик, что жидкости можно
считать практически несжимаемыми.
Иногда сжимаемость жидкостей полезна
- ее используют в гидравлических
амортизаторах и пружинах.
5) Вязкость жидкостей - свойство жидкости сопротивляться относительному движению (сдвигу) ее частиц, обусловливающее появление силы внутреннего трения между слоями жидкости, если последние имеют различные скорости движения. Это свойство характеризуется коэффициентами динамической и кинематической вязкостей.
Динамическая
вязкость
![]() - сила, которая возникает на единице
площади поверхности двух движущихся
друг относительно друга слоев жидкости
при градиенте скорости
- сила, которая возникает на единице
площади поверхности двух движущихся
друг относительно друга слоев жидкости
при градиенте скорости
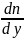 =1
(
=1
(
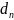 -
разность скоростей перемещающихся
слоев воды,
-
разность скоростей перемещающихся
слоев воды,
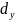 -
толщина слоя). В практике для характеристики
вязкости жидкости чаще применяют не
коэффициент динамической вязкости, а
коэффициент кинематической вязкости
n (м2/с или Стокс). 1 Ст=1 м2/с. Коэффициентом
кинематической вязкости называется
отношение коэффициента динамической
вязкости к плотности жидкости:
-
толщина слоя). В практике для характеристики
вязкости жидкости чаще применяют не
коэффициент динамической вязкости, а
коэффициент кинематической вязкости
n (м2/с или Стокс). 1 Ст=1 м2/с. Коэффициентом
кинематической вязкости называется
отношение коэффициента динамической
вязкости к плотности жидкости:
![]() Вязкость
капельных жидкостей при увеличении
температуры уменьшается, а вязкость
газов возрастает.
Вязкость
капельных жидкостей при увеличении
температуры уменьшается, а вязкость
газов возрастает.
Для измерения вязкости служат приборы, называемые вискозиметрами. Для определения вязкости капельных жидкостей широкое распространение получил вискозиметр Энглера, который представляет собой металлический цилиндрический сосуд объемом 200 см3, наполняемый сначала дистиллированной водой при температуре 20°С, а затем испытуемой жидкостью. Жидкость вытекает из сосуда через круглое отверстие диаметром около 3 мм. За вязкость по Энглеру принимается отношение времени t истечения 200 см3 испытуемой жидкости ко времени tB истечения того же объема дистиллированной воды при температуре 20°С, равному 51,6 с.
Таким образом, вязкость по Энглеру (условная вязкость в градусах Энглера), обозначаемая обычно °Е, определяется зависимостью
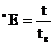
5. Что такое рабочие жидкости?
Рабочая жидкость (в гидроприводе) — жидкость, используемая как носитель энергии. В качестве рабочих жидкостей применяются минеральные, синтетические и полусинтетические масла, жидкости на силиконовой основе, водо-масляные эмульсии, масляно-водяные эмульсии.
Рабочие жидкости для гидросистем должны удовлетворять следующим требованиям: вязкостью в требуемом диапазоне значений; высоким индексом вязкости (минимальной зависимостью вязкости от температуры); хорошими смазывающими свойствами; химической инертностью к материалам, из которых сделаны элементы гидропривода; высоким объёмным модулем упругости; высокой устойчивостью к химической и механической деструкции; высоким коэффициентом теплопроводности и удельной теплоёмкости и малым коэффициентом теплового расширения; высокой температурой вспышки; нетоксичностью. Одна из функций рабочих жидкостей — защита деталей гидропривода от коррозии, поэтому рабочие жидкости обычно содержат антикоррозионные присадки. Другая функция рабочей жидкости — теплообмен между элементами гидросистемы, а также обмен теплом с окружающей средой. Также рабочие жидкости осуществляют надёжную смазку трущихся поверхностей деталей элементов гидросистемы.
6. понятие о гидростатическом давлении и его свойствах.
В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением. Рассмотрим произвольный объем жидкости, находящейся в равновесии под действием внешних сил.
Выделим внутри этого объема жидкости очень малую площадку ∆ώ. Действующая на эту площадку сила нормальна к ней, тогда соотношение
![]() представляет собой
"напряжение", т.е. силу, приходящуюся
на единицу площади.
представляет собой
"напряжение", т.е. силу, приходящуюся
на единицу площади.
Для получения точного значения р в данной точке надо определить предел этого отношения при ∆ώ→0 , что и определит гидростатическое давление в данной точке:
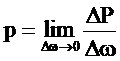 Размерность [р]
равна размерности напряжения, т.е.
сила/площадь;
[р]= [Па] или
[кгс/м2]
Размерность [р]
равна размерности напряжения, т.е.
сила/площадь;
[р]= [Па] или
[кгс/м2]
Свойства гидростатического давления
На поверхности жидкости гидростатическое давление всегда направлено по нормали внутрь рассматриваемого объема жидкости.
Гидростатическое давление в данной точке во всех направлениях одинаково (основная теорема гидростатики), т.е.
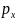 =
=
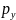 =
=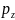 =p
=pГидростатическое давление в точке, будучи одинаковым по любому направлению, неодинаково в различных точках пространства, т.е. есть функция координат: Если давление Р отсчитывают от абсолютного нуля, то его называют абсолютным давлением Рабс. Если давление отсчитывают от атмосферного, то оно называется избыточным (манометрическим) Ризб. Оно измеряется манометром. Атмосферное давление постоянно Ратм = 103 кПа. Вакуумметрическое давление Рвак - недостаток давления до атмосферного. В технике в настоящее время продолжают применять систему единиц МКГСС, в которой за единицу давления принимается 1 кгс/м². 1 Па = 0,102 кгс/м² или 1 кгс/м² = 9,81 Па.
8. Дифференциальное уравнение поверхности равного давления
Поверхность, во всех точках которой значения гидростатического давления равны между собой, называют поверхностью равного давления или поверхностью уровня. На положение уровня свободной поверхности влияют силы тяжести и инерции.
Найдем величину равного давления Р по трем частным производным. При Р=const и р # 0 значение полного дифференциала dP=0 и, следовательно, уравнение поверхности жидкости равного давления имеет вид Xdx+Ydy+Zdz=0
Это уравнение называется уравнением поверхности жидкости равного или постоянного давления. Рассмотрим наиболее часто встречающиеся случаи.
Первый случай, когда на покоящуюся жидкость действует одна внешняя сила, сила тяжести, тогда X=0, Y=0, Z= -g (направление ускорения свободного падения не совпадает с положительным направлением оси Z). В этом случае исходное уравнение имеет вид
-gdz=0 или Z=const, т. е. получаем поверхности равного давления, представляющие собой семейство горизонтальных плоскостей. Каждому значению Zсоответствует плоскость, точки которой имеют определенное постоянное значение давления. Свободная поверхность жидкости (для ограниченного объема), в данном случае—одна из плоскостей равного давления. Имеем в виду, что свободная поверхность — это поверхность на границе жидкой и газообразной сред. На свободную поверхность будет приложено постоянное давление равное атмосферному.
9. Основное уравнение гидростатики.
Основным уравнением гидростатики называется уравнение:
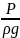 +
z=H=const,
+
z=H=const,
Где
P — гидростатическое давление (абсолютное или избыточное) в произвольной точке жидкости,
ρ — плотность жидкости,
g — ускорение свободного падения,
z — высота точки над плоскостью сравнения (геометрический напор),
H— гидростатический напор. Уравнение показывает, что гидростатический напор во всех точках покоящейся жидкости является постоянной величиной. Иногда основным законом гидростатики называют принцип Паскаля.
10. Законы гидростатики.
Гидростатика — раздел физики сплошных сред, изучающий равновесие жидкостей, в частности, в поле тяжести.
Прежде всего, полезно сравнить гидростатику с теорией упругости, изучающей равновесие твёрдых тел. В отличие от твёрдого тела, жидкость не «держит» сдвиговые напряжения. Именно поэтому в жидкости не может существовать анизотропии напряжений, а значит вместо многокомпонентного тензора, напряжения в жидкости описываются единственной величиной — давлением. Отсюда вытекает закон Паскаля: давление, оказываемое на жидкость, передаётся жидкостью одинаково во всех направлениях.
Основной закон гидростатики для толщи жидкости — зависимость давления от глубины, который для несжимаемой жидкости в однородном поле тяжести имеет вид P=ρgh . Из этого закона следует равенство уровней в сообщающихся сосудах, закон Архимеда: на тело, погружённое в жидкость, действует выталкивающая сила F=ρgV , где ρ — плотность жидкости, а V — объём тела, погруженного в жидкость.
Наглядно представить себе закон Архимеда можно следующим образом. Замена тела помещенного в жидкость на саму эту жидкость ничего не изменит для окружающей тело жидкости. При этом жидкость-заменитель будет невесомой, поскольку она идентична остальной жидкости и иной вес означал бы движение вверх или вниз и возможность получения энергии из ничего. А поскольку жидкость-заменитель «на воздухе» весила бы как раз столько, сколько положено по закону Архимеда, ρgV, то именно этот вес тело, погружённое в жидкость, теряет. Форма свободной поверхности жидкости определяется комбинацией внешних сил (прежде всего, сил тяготения) и сил поверхностного натяжения. Для больших масс жидкости преобладают силы тяготения, и свободная поверхность принимает форму эквипотенциальной поверхности, а при размерах порядка или меньше сантиметра (для пресной воды) определяющими являются капиллярные силы.
11. Понятие о вакуумном, абсолютном и манометрическом давлениях.
Если величину давления р отсчитывают от нуля, его называют абсолютным, если от атмосферного — избыточным – величина давления, превышающая атмосферное или манометрическим – величина давления, которое не достает до атмосферного.
Абсолютное давление равно атмосферному, сложенному с избыточным, т.е. Pабс=Рат+Ризб
Если гидромеханическое давление в жидкости оказывается меньше, атмосферного, то, как принято говорить, в жидкости имеется вакуум (разрежение).
Величина вакуума определяется разностью между атмосферным и абсолютным давлениями в жидкости Рвак = Рат – Рабс и изменяется в пределах от нуля до атмосферного давления.
12. Приборы для измерения давления.
Существует два основных типа приборов для измерения давления в жидкости.
К приборам первого типа можно отнести пьезометры. Они представляют собой вертикальную трубку, обычно прозрачную. Если, например, нужно измерить давление в точке a, то достаточно подсоединить эту трубку к стенке сосуда так чтобы её конец находился на поверхности равного давления, проходящей через эту точку. В пьезометре установится уровень жидкости, пропорциональный давлению в т. a.
Ко второму типу приборов относятся манометры, которые имеют большое разнообразие по типам размерам и характеристикам. Однако принципиально все эти приборы состоят из чувствительного элемента, который меняет свою форму под воздействием давления, и, связанного с этим элементом, передаточного механизма и регистрирующего прибора (индикатора).
Подсоединять манометры для измерения давления в определённой точке надо также как пьезометры, на уровне поверхности равного с выбранной точкой, давления. Например, под действием давления гибкий чувствительный элемент – мембрана изгибается. Размер этого отклонения пропорционален величине измеряемого давления. Вместе с мембраной отклоняется жёстко соединённая с ней стрелка, которая перемещается вдоль шкалы. Такой прибор отличается небольшим отклонением регистрирующего элемента – стрелки, следовательно, точность измерения большой быть не может.
Для увеличения чувствительности прибора мембрану можно соединить с зубчатой рейкой, находящейся в зацеплении с шестерней. Если с последней жёстко соединить стрелку, то при изменении давления она будет поворачиваться по отношению к круговой шкале. В этом случае изгиб мембраны даст большее, чем в первом случае, линейное отклонение конца стрелки. Это увеличит точность показаний прибора.
Общим недостатком таких приборов является малое исходное отклонение чувствительного элемента – мембраны.
Для устранения этого недостатка используются более сложные чувствительные элементы. Чаще всего таким элементом является полая трубка, согнутая по окружности. Один конец трубки связан со штуцером для подключения к измеряемому давлению, другой с зубчатым сектором, который связан с шестерней и стрелкой, поворачивающейся вокруг шкалы. При повышении давления трубка разгибается, и это отклонение значительно больше, чем отклонение мембраны при таком же давлении.
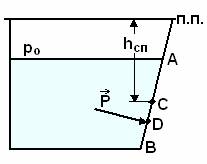
13. Сила давления жидкости на плоские и криволинейные поверхности.
Если твердая плоская стенка АВ с одной стороны соприкасается с жидкостью, а с другой находится под воздействием атмосферного давления, то величина равнодействующей силы давления жидкости (с учетом внешнего атмосферного давления) на смоченную часть твердой поверхности равна:
Р =g hcп = pс ,
где hсп — расстояние от пьезометрической поверхности до центра тяжести С смоченной части стенки; рс - избыточное давление в центре тяжести, - площадь смоченной поверхности АВ. Точка приложения равнодействующей сил давления называется центром давления. Она определяется как:
![]() где
где
![]() -
момент инерции плоской смоченной фигуры
относительно горизонтальной оси (табл.),
проходящей через ее центр тяжести; yD
, ус
- расстояния
до центров давления и тяжести, измеряемые
вдоль продольной оси симметрии (или ее
продолжения) фигуры от пьезометрической
поверхности.
-
момент инерции плоской смоченной фигуры
относительно горизонтальной оси (табл.),
проходящей через ее центр тяжести; yD
, ус
- расстояния
до центров давления и тяжести, измеряемые
вдоль продольной оси симметрии (или ее
продолжения) фигуры от пьезометрической
поверхности.
Давление жидкости на криволинейную твердую стенку
Р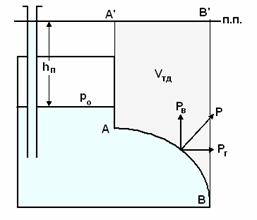 езультирующая
сила давления жидкости на криволинейную
твердую стенку Р может быть определена
по ее проекциям на оси координат Рх,
Ру,
Рz,
где Рх,
Ру
– горизонтальные составляющие, -
вертикальная составляющая силы давления
Р.
езультирующая
сила давления жидкости на криволинейную
твердую стенку Р может быть определена
по ее проекциям на оси координат Рх,
Ру,
Рz,
где Рх,
Ру
– горизонтальные составляющие, -
вертикальная составляющая силы давления
Р.
Величина горизонтальной составляющей силы давления равна
PГ=рcSB
где SB - проекция криволинейной поверхности на вертикальную плоскость, нормальную к искомой составляющей силы Р,
рc – результирующее давление в центре тяжести этой проекции.
Сила РГ проходит через центр давления, положение которого определяется аналогично случаю плоских стенок. Линия действия силы Р проходит через точку пересечения линий действия сил РГ и РВ . Линия, действия горизонтальных составляющих силы давления проходит через центры давления соответствующих проекций криволинейной поверхности SB. Вертикальная составляющая силы давления жидкости на криволинейную поверхность может быть найдена из выражения
PB= gVтд, где Vтд – объем «тела давления», образованного криволинейной поверхностью, ее проекцией на пьезометрическую поверхность, и соединяющими их вертикальными образующими
Линия действия вертикальной составляющей РB силы давления проходит через центр тяжести «тела давления». Вертикальная сила давления РB направлена вверх, если этот объем «тела давления» строится со стороны несмоченной части стенки, и вниз - если объем этого тела строится со стороны смоченной части стенки.
14. Примеры относительного покоя жидкости.
Относительный покой жидкости в цилиндре, вращающемся вокруг вертикальной оси .
При равномерном вращении цилиндра с жидкостью вокруг вертикальной оси жидкость через некоторое время начинает вращаться вместе с сосудом, т.е. приходит в состояние относительного покоя. В этом состоянии отсутствует смещение частичек жидкости относительно друг друга и стенок цилиндра, и вся массе жидкости с цилиндром вращается как твердое тело. С относительным покоем жидкости во вращающихся сосудах приходится часто встречаться на практике (например, в сепараторах и центрифугах, применяемых для разделения жидкостей, а также в приборах для определения и регулирования чисел оборотов). При этом, как правило, решаются два типа задач. Первая задача связана с расчетом на прочность стенок сосуда. Для этого необходимо знать закон распределения давления в жидкости. Вторая задача связана с расчетом объема и габаритных размеров сосуда (например, жидкостного тахометра). В этом случае нужно уметь рассчитывать координаты точек свободной поверхности.
15. Условие плавания тел. Остойчивость тела(ρм, l, hм)
На твердое тело, погруженное в жидкость, действуют архимедова сила FA и сила тяжести mg. В зависимости от соотношения сил mg и FA тело может тонуть, плавать и всплывать. Если mg > FA, тело тонет; если mg = FA, то тело плавает внутри жидкости или на ее поверхности; если mg < FA, то тело всплывает до тех пор, пока архимедова сила и сила тяжести не сравняются по модулю. Тело плавает на поверхности, если рж = рт; тело тонет, если рт > рж; тело всплывает, если рт < рж. Остойчивость — способность плавающего тела, выведенного из равновесия, восстанавливать исходное положение после прекращения действия сил, вызывающих крен. В случае воздействия на плавающее тело внешних сил (ветра, крутого поворота) оно будет отклоняться от положения равновесия (давать крен). При остойчивом плавании тела центр тяжести расположен ниже центра водоизмещения, а после прекращения взаимодействия этих сил тело возвращается в прежнее положение.
16. Основные определения. Линия тока, трубка тока, элементарная струйка, элементарный расход. Расход целого потока.
Линия тока - кривая, проведенная через ряд точек в движущейся жидкости таким образом, что в каждой из этих точек в данный момент времени векторы скорости являются касательными к кривой. Следует различать линию тока и траекторию. Последняя характеризует путь, проходимый одной определенной частицей. Линия тока характеризует направление движения в данный момент времени различных лежащих на ней частиц. При установившемся движении линии тока совпадают с траекториями частиц жидкости. При неустановившемся движении они не совпадают, так как каждая частица жидкости лишь одно мгновение находится на линии тока, которая сама существует лишь одно мгновение. В следующий момент существуют другие линии тока, на одной из которых будет располагаться частица, и т.д. Если выделить в движущейся жидкости достаточно малый контур, ограничивающий элементарно малую площадку Δs, то поверхность, образуемая линиями тока, проходящими через все точки этого контура, выделяет трубку тока. Если же через все точки площадки Δs провести линий тока, то полученный объемный пучок линии тока будет называться элементарной струйкой жидкости. Таким образом, элементарная струйка жидкости заполняет трубку тока и ограничена линиями тока, проходящими через точки выделенного контура с площадью Δs. При неустановившемся движении непрерывно изменяются форма и местоположение элементарных струек. Элементарные струйки жидкости при установившемся движении обладают следующими свойствами: площадь поперечного сечения струйки и ее форма с течением времени не изменяются, так как не изменяются формы линий токов; перетекание жидкости через боковую поверхность элементарной струйки не происходит; во всех точках поперечного сечения элементарной струйки скорости движения одинаковы вследствие малости площади поперечного сечения.
Форма, площадь поперечного сечения элементарной струйки и скорости в различных поперечных сечениях струйки могут изменяться. Живым сечением струйки называется элементарно малая площадка Δs, представляющая собой поперечное сечение струйки, перпендикулярное линиям тока. Расход элементарной струйки - объем жидкости, проходящей через живое сечение струйки в единицу времени. В гидравлике рассматривается струйчатая модель движения жидкости, т.е. поток считается состоящим из совокупности элементарных струек, имеющих различные скорости.
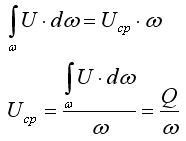 Тогда
расход целого потока можно представить
через среднюю расходную скорость:
Q=Uср*ώ.
Тогда
расход целого потока можно представить
через среднюю расходную скорость:
Q=Uср*ώ.
17. Режимы движения жидкости.
Различаются два режима движения жидкости — ламинарный и турбулентный. При ламинарном движении жидкость движется послойно, т.е. слои жидкости не перемешиваются, что можно наблюдать при движении подкрашенной жидкости в стеклянной трубке. Такое движение происходит до определенной скорости. При превышении этой скорости слои жидкости перемешиваются, движение становится беспорядочным или турбулентным. Скорость, при которой происходит переход ламинарного потока в турбулентный, называют критической. Эта скорость зависит от геометрической характеристики сечения (диаметра трубы) и вязкости жидкости. Если при ламинарном режиме потери давления пропорциональны скорости потока, то при турбулентном — квадрату этой скорости; значит, при прочих равных условиях эти потери выше.
18. Число Рейнольса.
Число,
или, правильнее, критерий Рейно́льдса
(![]() ),
— безразмерная величина, характеризующая
отношение нелинейного и диссипативного
членов в уравнении Навье — Стокса. Число
Рейнольдса также считается критерием
подобия течения вязкой жидкости.
),
— безразмерная величина, характеризующая
отношение нелинейного и диссипативного
членов в уравнении Навье — Стокса. Число
Рейнольдса также считается критерием
подобия течения вязкой жидкости.
Число Рейнольдса определяется следующим соотношением:
 =
=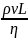 =
=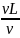 =
=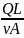 ,
где
ρ
— плотность среды, кг/м3; V—
характерная скорость, м/с; L
— характерный размер, м; η
— динамическая вязкость среды, Н·с/
,
где
ρ
— плотность среды, кг/м3; V—
характерная скорость, м/с; L
— характерный размер, м; η
— динамическая вязкость среды, Н·с/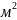 ;
ν
— кинематическая вязкость среды,
/с(ν=
;
ν
— кинематическая вязкость среды,
/с(ν=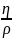 );
Q
— объёмная скорость потока; A
— площадь сечения трубы. Для
каждого вида течения существует
критическое число Рейнольдса,
);
Q
— объёмная скорость потока; A
— площадь сечения трубы. Для
каждого вида течения существует
критическое число Рейнольдса,
 ,
которое, как принято считать, определяет
переход от ламинарного течения к
турбулентному. При Re<
течение происходит в ламинарном режиме,
при Re>
возможно возникновение турбулентности.
Критическое значение числа Рейнольдса
зависит от конкретного вида течения
(течение в круглой трубе, обтекание шара
и т. п.), различными возмущениями потока,
как-то изменение направленности и модуля
вектора скорости потока, шероховатость
стенок, близость местных сопротивлений
и др. Число
Рейнольдса как критерий перехода от
ламинарного к турбулентному режиму
течения и обратно относительно хорошо
действует для напорных потоков. При
переходе к безнапорным потокам переходная
зона между ламинарным и турбулентным
режимами возрастает, и использование
числа Рейнольдса как критерия не всегда
правомерно. Например, в водохранилищах
формально вычисленные значения числа
Рейнольдса очень велики, хотя там
наблюдается ламинарное течение. Напротив,
возмущения потока могут значительно
снижать величину
.
Стоит отметить, что для газов Reкр
достигается при значительно больших
скоростях, чем у жидкостей, поскольку
у первых куда больше кинематическая
вязкость (в 10-15 раз).
,
которое, как принято считать, определяет
переход от ламинарного течения к
турбулентному. При Re<
течение происходит в ламинарном режиме,
при Re>
возможно возникновение турбулентности.
Критическое значение числа Рейнольдса
зависит от конкретного вида течения
(течение в круглой трубе, обтекание шара
и т. п.), различными возмущениями потока,
как-то изменение направленности и модуля
вектора скорости потока, шероховатость
стенок, близость местных сопротивлений
и др. Число
Рейнольдса как критерий перехода от
ламинарного к турбулентному режиму
течения и обратно относительно хорошо
действует для напорных потоков. При
переходе к безнапорным потокам переходная
зона между ламинарным и турбулентным
режимами возрастает, и использование
числа Рейнольдса как критерия не всегда
правомерно. Например, в водохранилищах
формально вычисленные значения числа
Рейнольдса очень велики, хотя там
наблюдается ламинарное течение. Напротив,
возмущения потока могут значительно
снижать величину
.
Стоит отметить, что для газов Reкр
достигается при значительно больших
скоростях, чем у жидкостей, поскольку
у первых куда больше кинематическая
вязкость (в 10-15 раз).
19. Виды движения жидкости.
Неустановившееся движение - такое, при котором в каждой данной точке пространства скорость движения и гидродинамическое давление с течением времени изменяются, т.е. можно записать, что u и p зависят не только от местонахождения точки, но и от времени, в течение которого рассматривается движение. u= f1(x,y,z,t);p= f2(x,y,z,t). Установившееся движение - такое, при котором в каждой точке скорость и гидродинамическое давление с течением времени не изменяются, но в разных точках они могут быть различными, т.е. u и p зависят только от координат рассматриваемых точек: u = φ1(x,y,z); p = φ2(x,y,z). Установившееся движение наблюдается, например, при истечении воды из резервуара при неизменной отметке свободной поверхности. Установившееся движение подразделяется на равномерное и неравномерное. Равномерное движение характеризуется тем, что скорости, форма и площадь сечения потока не изменяются по длине. Неравномерное движение отличается изменяемостью скоростей, глубин, площадей сечений потока по его длине. Из неравномерных движений следует отметить плавно изменяющиеся движения, характеризующееся тем, что: а) линии тока имеют малую кривизну; б) линии тока почти параллельны, вследствие чего живое сечение можно считать плоским; в) давления в плоскости живого сечения распределяются по гидростатическому закону. Напорное движение происходит в тех случаях, когда поток ограничен твердыми поверхностями со всех сторон, при этом в любой точке потока гидродинамическое давление отличается от атмосферного и может быть больше или меньше атмосферного. Движение в этом случае происходит под действием давления (напора), создаваемого, например, насосом или водонапорной башней, - движение в водопроводных и других трубах. Безнапорное движение отличается тем, что поток имеет свободную поверхность, находящуюся под атмосферным давлением. Безнапорное движение происходит под действием сил тяжести.
20. Элементы потока.
Площадь живого сечения потока (м2) — это площадь поперечного сечения потока, перпендикулярная линиям тока. Расход потока q (или Q) — это объём жидкости V, проходящей через живое сечение потока в единицу времени t: q = V/t. Единицы измерения расхода в СИ м3/с, а в других системах: м3/ч , м3/сут, л/с. Средняя скорость потока v (м/с) — это частное от деления расхода потока на площадь живого сечения : v = q/. Отсюда расход можно выразить так: q = v . Скорости потоков воды в сетях водопровода и канализации зданий обычно порядка 1 м/с. Следующие два термина относятся к безнапорным потокам. Смоченный периметр (м) — это часть периметра живого сечения потока, где жидкость соприкасается с твёрдыми стенками. Например, на рис. 7,в величиной является длина дуги окружности, которая образует нижнюю часть живого сечения потока и соприкасается со стенками трубы. Гидравлический радиус R (м) — это отношение вида R = / , которое применяется в качестве расчётного параметра в формулах для безнапорных потоков.
21. Вывод уравнения Бернулли для элементарной струйки и целого потока.
Уравнение Бернулли для элементарной струйки идеальной жидкости
![]()
Уравнение Бернулли для элементарной струйки реальной жидкости
![]()
Уравнение Бернулли для потока реальной жидкости
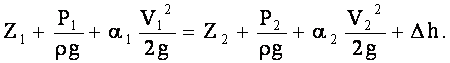
22.ИНТЕРПРЕТАЦИЯ УРАВНЕНИЯ БЕРНУЛИ Все члены уравнения Бернулли имеют линейную размерность и представляют собой напоры:
z - называется геометрическим напором (геометрической высотой), представляет собой место положения центра тяжести живого сечения элементарной струйки относительно плоскости сравнения,
![]() -
называется пьезометрическим напором
(пьезометрической высотой) представляет
собой высоту, на которую могла бы
подняться жидкость при отсутствии
движения
-
называется пьезометрическим напором
(пьезометрической высотой) представляет
собой высоту, на которую могла бы
подняться жидкость при отсутствии
движения
![]() -
носит название скоростного напора.
-
носит название скоростного напора.
![]() -
носит название гидродинамического
напора
-
носит название гидродинамического
напора
Уравнение
Бернулли является выражением закона
сохранения механической энергии
движущейся жидкости, по этой причине
все части уравнения представляют собой
величины удельной энергии жидкости:
z - удельная энергия положения,
![]() -
удельная энергия давления,
-
удельная энергия давления,
![]() -
удельная потенциальная энергия,
-
удельная потенциальная энергия,
![]() -
удельная кинетическая энергия
-
удельная кинетическая энергия
![]() -
удельная механическая энергия.
-
удельная механическая энергия.
23. Характеристика ламинарного режима движения.
Стокса
формула имеет
вид:
![]() ,
причём направление обхода контура
L должно
быть согласовано с ориентацией поверхности
S. В векторной форме Стокса
формула
приобретает вид:
,
причём направление обхода контура
L должно
быть согласовано с ориентацией поверхности
S. В векторной форме Стокса
формула
приобретает вид:
![]() ,где
а = Pi
+ Qj
+ Rk, dr —
элемент контура L,
ds — элемент
поверхности S, n
—единичный вектор внешней нормали к
этой поверхности. Формула Пуазейля.При
установившемся ламинарном движении
вязкой несжимаемой жидкости сквозь
цилиндрическую трубу круглого сечения
секундный объёмный расход прямо
пропорционален перепаду давления на
единицу длины трубы и четвертой степени
радиуса и обратно пропорционален
коэффициенту
вязкости жидкости.
,где
а = Pi
+ Qj
+ Rk, dr —
элемент контура L,
ds — элемент
поверхности S, n
—единичный вектор внешней нормали к
этой поверхности. Формула Пуазейля.При
установившемся ламинарном движении
вязкой несжимаемой жидкости сквозь
цилиндрическую трубу круглого сечения
секундный объёмный расход прямо
пропорционален перепаду давления на
единицу длины трубы и четвертой степени
радиуса и обратно пропорционален
коэффициенту
вязкости жидкости.
![]() где
где
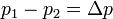 —
перепад давления
на концах капилляра, Па;
—
перепад давления
на концах капилляра, Па;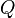 —
секундный объёмный
расход жидкости, м³/с;
—
секундный объёмный
расход жидкости, м³/с;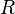 —
радиус
капилляра, м;
—
радиус
капилляра, м;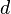 —
диаметр
капилляра, м;
—
диаметр
капилляра, м;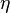 —
коэффициент
динамической вязкости, Па·с;
—
коэффициент
динамической вязкости, Па·с;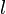 —
длина
трубы, м.
—
длина
трубы, м.
Формула
Дарси –Вейсбаха где![]()
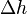 —
потери напора на
гидравлическом сопротивлении;
—
потери напора на
гидравлическом сопротивлении;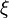 —
коэффициент потерь
(коэффициент Дарси);
—
коэффициент потерь
(коэффициент Дарси);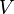 —
средняя скорость
течения жидкости;
—
средняя скорость
течения жидкости;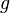 —
ускорение свободного
падения;
—
ускорение свободного
падения;величина
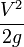 называется
скоростным (или динамическим) напором.
называется
скоростным (или динамическим) напором.
Формула Вейсбаха, определяющая потери давления на гидравлических сопротивлениях, имеет вид:
![]() где
где![]() —
потери давления на гидравлическом
сопротивлении; ρ—
плотность жидкости.
—
потери давления на гидравлическом
сопротивлении; ρ—
плотность жидкости.
Если
гидравлическое сопротивление представляет
собой участок трубы длиной
![]() и
диаметром
и
диаметром
![]() ,
то коэффициент Дарси определяется
следующим образом:
,
то коэффициент Дарси определяется
следующим образом:
![]()
где
![]() —
коэффициент потерь на трение по длине.
—
коэффициент потерь на трение по длине.
Тогда
формула Дарси приобретает вид:
![]() или для потери давления:
или для потери давления:
![]()
24.Характеристика турбулентного режима движения. По характеру движения частицы жидкости в турбулентном потоке ведут себя примерно так, как молекулы в представлении кинетической теории газов: они находятся в состоянии беспорядочного хаотического движения. В случае, например, трубопроводов с этим связано существенное возрастание потерь энергии при движении жидкости по сравнению с ламинарным потоком. В турбулентном режиме происходит выравнивание эпюры распределения скоростей по сечению потока. С турбулентным движением связано так же усиление теплопередачи внутри жидкости. Перемешивание определяется наличием в турбулентном потоке уже упомянутых выше, перпендикулярных основному направлению движения жидкости составляющих скоростей. Перемешивание в турбулентно движущейся жидкости приводит к взвешиванию находящейся в потоке в дисперсном состоянии фракции другой фазы (твердые, газообразные и т. п.). Турбулентное движение по самой своей сущности является движением неустановившимся; все гидравлические характеристики и, в частности, скорости в каждой точке занятого турбулентным потоком пространства изменяются с течением времени. Таким образом, турбулентное движение можно определить как движение жидкости с пульсацией скоростей, приводящей к перемешиванию жидкости.
25. Если высота выступов шероховатости Δ меньше, чем толщина ламинарной пленки (Δ <δ), то в этом случае шероховатость стенок не влияет на характер движения и соответственно потери напора не зависят от шероховатости, а стенки называются гидравлически гладкими. Когда высота выступов шероховатости превышает толщину ламинарной пленки (Δ <δ), то потери напора зависят от шероховатости, и такие трубы называются гидравлически шероховатыми.
26. Формулы для определения коэффициента сопротивления трения по длине.
Формула
Шези — формула для определения средней
скорости потока при установившемся
равномерном турбулентном движении
жидкости в области квадратичного
сопротивления для случая безнапорного
потока. Опубликована французским
инженером-гидравликом А. Шези в 1769 году.
Применяется для расчётов потоков в
речных руслах и канализационых системах.
V=C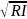 ,
где V — средняя скорость потока, м/с; C —
коэффициент сопротивления трения по
длине (коэффициент Шези), являющийся
интегральной характеристикой сил
сопротивления; R — гидравлический
радиус, м;
,
где V — средняя скорость потока, м/с; C —
коэффициент сопротивления трения по
длине (коэффициент Шези), являющийся
интегральной характеристикой сил
сопротивления; R — гидравлический
радиус, м;
I — гидравлический уклон м/м. Формула Шези имеет то же предназначение, что и формула Дарси-Вейсбаха. Коэффициент потерь на трение связан с коэффициентом сопротивления C следующей зависимостью:
C=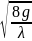
Коэффициент сопротивления C может быть определён по формуле Н. Н. Павловского:
C=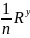 где
n — коэффициент шероховатости
где
n — коэффициент шероховатости
31. Последовательное и параллельное соединение трубопроводов.
Основным элементом любой трубопроводной системы, какой бы сложной она ни была, является простой трубопровод. Классическим определением его будет - простым трубопроводом является трубопровод, собранный из труб одинакового диаметра и качества его внутренних стенок, в котором движется транзитный поток жидкости, и на котором нет местных гидравлических сопротивлений. При напорном движении жидкости простой трубопровод работает полным сечением.
Размер сечения трубопровода (диаметр или величина гидравлического радиуса), а также его протяжённость (длина) трубопровода (/, L) являются основными геометрическими характеристиками трубопровода. Основными технологическими характеристиками трубопровода являются расход жидкости в трубопроводе Q и напор H(на головных сооружениях трубопровода, т.е. в его начале). Большинство других характеристик простого трубопровода являются, не смотря на их важность, производными характеристиками. Поскольку в простом трубопроводе расход жидкости транзитный (одинаковый в начале и конце трубопровода), то средняя скорость движения жидкости в трубопроводе постоянна V=const . Для установившегося движения жидкости по трубопроводу средняя скорость движения жидкости определяется по формуле Шези:
![]() где:
где:
![]() - скоростной коэффициент Шези,
- скоростной коэффициент Шези,
![]() - гидравлический
радиус сечения, для круглого сечения
при полном заполнении жидкостью
- гидравлический
радиус сечения, для круглого сечения
при полном заполнении жидкостью
![]()
![]() - гидравлический
уклон. Полагая, что весь имеющийся напор
на головных сооружениях (в начале)
трубопровода тратится на преодоление
сил трения в трубопроводе (в простом
трубопроводе это потери напора по длине
- гидравлический
уклон. Полагая, что весь имеющийся напор
на головных сооружениях (в начале)
трубопровода тратится на преодоление
сил трения в трубопроводе (в простом
трубопроводе это потери напора по длине
![]() ),
уравнение движения жидкости (Бернулли)
примет вид:
),
уравнение движения жидкости (Бернулли)
примет вид:
![]() График
уравнения простого трубопровода носит
название его гидравлической характеристики.
Вид гидравлической характеристики
зависит от режима движения жидкости в
трубопроводе: при ламинарном движении
жидкости гидравлическая характеристика
трубопровода - прямая линия, проходящая
через начало координат. При турбулентном
режиме гидравлическая характеристика
- парабола.
График
уравнения простого трубопровода носит
название его гидравлической характеристики.
Вид гидравлической характеристики
зависит от режима движения жидкости в
трубопроводе: при ламинарном движении
жидкости гидравлическая характеристика
трубопровода - прямая линия, проходящая
через начало координат. При турбулентном
режиме гидравлическая характеристика
- парабола.
Параллельное соединение.
Отличительной
особенностью таких трубопроводов
является то, что поток жидкости делится
в одной точке на несколько самостоятельных
потоков, которые позже сходятся в другой
точке. Каждый из этих потоков может
содержать свои местные сопротивления.
Наиболее часто возникающей задачей,
связанной с расчётом таких трубопроводов,
является определение расхода в каждой
ветви. Рассмотрим движение жидкости по
этим трубопроводам, считая, что
потенциальная энергия положения много
меньше потенциальной энергии сжатия,
которая определяется давлением, и ею
можно пренебречь. Если считать, что в
местах разветвления и соединения
трубопроводов, обозначенных буквами н
и к, расход одинаков, а давления равны
Pн
и Pк
, то можно записать: Q=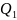 +
+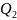 +
+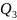
Особенность расчета заключается в том, что потери напора в каждой из линий одинаковы и равны разности напоров в узлах а и б.
h1= h2 = h3 = ... = hn = hA - hB=H
Расход
через любую из линий, соединяющих точки
А и В, может быть записан в виде:
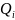 =
=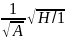
Так как сумма расходов во всех параллельных трубопроводах равна расходу Q до разветвления трубопровода
+
+
+…+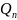 =
=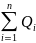 =Q;
Q=
=Q;
Q=
32. Насосная раздача.
Трубопровод с насосной подачей жидкости может быть разомкнутым, т.е. по которому жидкость перекачивается из одной емкости в другую, или замкнутым (кольцевым), в котором циркулирует одно и то же количество жидкости.
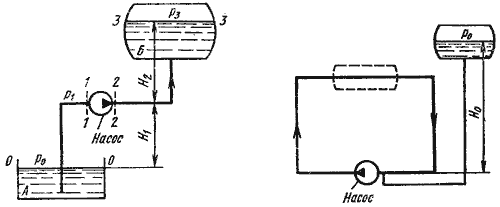
Рассмотрим трубопровод, по которому перекачивают жидкость из нижнего резервуара с давлением P 0 в другой резервуар с давлением P3. Высота расположения оси насоса H1 называется геометрической высотой всасывания, а трубопровод, по которому жидкость поступает к насосу, всасывающим трубопроводом или линией всасывания. Высота расположения конечного сечения трубопровода H2 называется геометрической высотой нагнетания, а трубопровод, по которому жидкость движется от насоса, напорным или линией нагнетания. Составим уравнением Бернулли для потока рабочей жидкости во всасывающем трубопроводе, т.е. для сечений 0-0 и 1-1 (принимая α = 1):
![]() Это уравнение
является основным для расчета всасывающих
трубопроводов.
Это уравнение
является основным для расчета всасывающих
трубопроводов.
Теперь рассмотрим напорный трубопровод, для которого запишем уравнение Бернулли, т.е. для сечений 2-2 и 3-3:
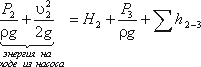 Левая часть этого
уравнения представляет собой энергию
жидкости на выходе из насоса. А на входе
насоса энергию жидкости можно будет
аналогично выразить из уравнения:
Левая часть этого
уравнения представляет собой энергию
жидкости на выходе из насоса. А на входе
насоса энергию жидкости можно будет
аналогично выразить из уравнения:
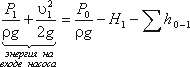 Таким образом,
можно подсчитать приращение энергии
жидкости, проходящей через насос. Эта
энергия сообщается жидкости насосом и
поэтому обозначается обычно Hнас.
Таким образом,
можно подсчитать приращение энергии
жидкости, проходящей через насос. Эта
энергия сообщается жидкости насосом и
поэтому обозначается обычно Hнас.
Для нахождения напора Hнас вычислим уравнение :
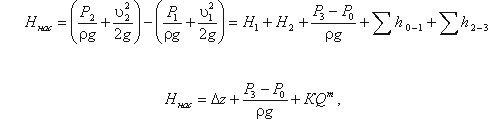
где Δz - полная геометрическая высота подъема жидкости, Δz = H 1 + H2; КQm - сумма гидравлических потерь,
P3 и Р0 - давление в верхней и нижней емкости соответственно.
Если к действительной разности уровней Δz добавить разность пьезометрических высот ( P3 - Р0 ) ( ρg ), то можно рассматривать увеличенную разность уровней
![]() и формулу можно
переписать так: Hнас = Hст + KQm Из этой
формулы делаем вывод, что Hнас = Hпотр
и формулу можно
переписать так: Hнас = Hст + KQm Из этой
формулы делаем вывод, что Hнас = Hпотр
Отсюда вытекает следующее правило устойчивой работы насоса: при установившемся течении жидкости в трубопроводе насос развивает напор, равный потребному. Характеристикой насоса называется зависимость напора, создаваемого насосом, от его подачи (расхода жидкости) при постоянной частоте вращения вала насоса.
34. Гидравлический удар в трубах. Расчетные формулы.
Гидравлический удар (гидроудар) — скачок давления в какой-либо системе, заполненной жидкостью, вызванный крайне быстрым изменением скорости потока этой жидкости за очень малый промежуток времени. Может возникать вследствие резкого закрытия или открытия задвижки. В первом случае гидроудар называют положительным, во втором - отрицательным. Опасен положительный гидроудар. При положительном гидроударе несжимаемую жидкость следует рассматривать как сжимаемую. Гидравлический удар способен вызывать образование продольных трещин в трубах, что может привести к их расколу, или повреждению других элементов трубопровода. Также гидроудары чрезвычайно опасны и для другого оборудования, такого как теплообменники, насосы и сосуды, работающие под давлением. Для предотвращения гидроударов, вызванных резкой переменой направления потока рабочей среды, на трубопроводах устанавливаются обратные клапаны.
Гидроударом также ошибочно называют следствие заполнения надпоршневого пространства в поршневом двигателе водой, вследствие чего поршень, не дойдя до мёртвой точки, начинает сжимать жидкость, что приводит к внезапной остановке и поломке мотора (излому шатуна или штока, обрыву шпилек головки цилиндра, разрыву прокладки).
Увеличение давления при гидравлическом ударе определяется в соответствии с его теорией по формуле:
![]() ,
где
,
где
 — увеличение давления в Н/м², ρ
— плотность жидкости в кг/м³,
— увеличение давления в Н/м², ρ
— плотность жидкости в кг/м³,
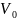 и
и
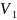 — средние скорости в трубопроводе до
и после закрытия задвижки (запорного
клапана) в м/с; с — скорость распространения
ударной волны вдоль трубопровода.
Жуковский доказал, что скорость
распространения ударной волны c
находится в прямо пропорциональной
зависимости от сжимаемости жидкости,
величины деформации стенок трубопровода,
определяемой модулем упругости материала
E,
из которого он выполнен, а также от
диаметра трубопровода. Следовательно,
гидравлический удар не может возникнуть
в трубопроводе, содержащем газ, так как
газ легко сжимаем. Зависимость между
скоростью ударной волны c,
её длиной и временем распространения
(L
и Ƭ
соответственно) выражается следующей
формулой:
— средние скорости в трубопроводе до
и после закрытия задвижки (запорного
клапана) в м/с; с — скорость распространения
ударной волны вдоль трубопровода.
Жуковский доказал, что скорость
распространения ударной волны c
находится в прямо пропорциональной
зависимости от сжимаемости жидкости,
величины деформации стенок трубопровода,
определяемой модулем упругости материала
E,
из которого он выполнен, а также от
диаметра трубопровода. Следовательно,
гидравлический удар не может возникнуть
в трубопроводе, содержащем газ, так как
газ легко сжимаем. Зависимость между
скоростью ударной волны c,
её длиной и временем распространения
(L
и Ƭ
соответственно) выражается следующей
формулой:
![]() В зависимости от
времени распространения ударной волны
и времени перекрытия задвижки (или
другой запорной арматуры) t,
в результате которого возник гидроудар,
можно выделить 2 вида ударов: Полный
(прямой) гидравлический удар, если t
< Ƭ
Неполный (непрямой) гидравлический
удар, если t.
> Ƭ
При полном гидроударе фронт возникшей
ударной волны движется в направлении,
обратном первоначальному направлению
движения жидкости в трубопроводе. Его
дальнейшее направление движения зависит
от элементов трубопровода, расположенных
до закрытой задвижки. Возможно и повторное
неоднократное прохождения фронта волны
в прямом и обратном направлениях. При
неполном гидроударе фронт ударной волны
не только меняет направление своего
движения на противоположное, но и
частично проходит далее сквозь не до
конца закрытую задвижку.
В зависимости от
времени распространения ударной волны
и времени перекрытия задвижки (или
другой запорной арматуры) t,
в результате которого возник гидроудар,
можно выделить 2 вида ударов: Полный
(прямой) гидравлический удар, если t
< Ƭ
Неполный (непрямой) гидравлический
удар, если t.
> Ƭ
При полном гидроударе фронт возникшей
ударной волны движется в направлении,
обратном первоначальному направлению
движения жидкости в трубопроводе. Его
дальнейшее направление движения зависит
от элементов трубопровода, расположенных
до закрытой задвижки. Возможно и повторное
неоднократное прохождения фронта волны
в прямом и обратном направлениях. При
неполном гидроударе фронт ударной волны
не только меняет направление своего
движения на противоположное, но и
частично проходит далее сквозь не до
конца закрытую задвижку.
Прямой гидравлический удар бывает тогда когда время закрытия задвижки t3 меньше фазы удара T, определяемой по формуле:
![]() Здесь L
- длина трубопровода от места удара до
сечения, в котором поддерживается
постоянное давление, Cu
- скорость распространения ударной
волны в трубопроводе, определяется по
формуле Н.Е. Жуковского, м/с:
Здесь L
- длина трубопровода от места удара до
сечения, в котором поддерживается
постоянное давление, Cu
- скорость распространения ударной
волны в трубопроводе, определяется по
формуле Н.Е. Жуковского, м/с:
Cu=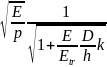 где E
- модуль объемной упругости жидкости,
p
- плотность жидкости,
где E
- модуль объемной упругости жидкости,
p
- плотность жидкости,
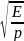 - скорость распространения звука в
жидкости,
- скорость распространения звука в
жидкости,
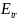 -
модуль упругости материала стенок
трубы, D
- диаметр трубы, h
- толщина стенок трубы.
-
модуль упругости материала стенок
трубы, D
- диаметр трубы, h
- толщина стенок трубы.
Для
воды отношение
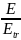 зависит от материала труб и может быть
принято; для стальных - 0.01; чугунных -
0.02; ж/б - 0.1-0.14; асбестоцементных - 0.11;
полиэтиленовых - 1-1.45
зависит от материала труб и может быть
принято; для стальных - 0.01; чугунных -
0.02; ж/б - 0.1-0.14; асбестоцементных - 0.11;
полиэтиленовых - 1-1.45
Коэффициент k для тонкостенных трубопроводов применяется (стальные, чугунные, а/ц, полиэтиленовые) равным 1. Для ж/б
![]()
![]() коэффициент
армирования кольцевой арматурой ( -
площадь сечения кольцевой арматуры на
1м длины стенки трубы). Обычно Повышение
давления при прямом гидравлическом
ударе определяется по формуле:
коэффициент
армирования кольцевой арматурой ( -
площадь сечения кольцевой арматуры на
1м длины стенки трубы). Обычно Повышение
давления при прямом гидравлическом
ударе определяется по формуле:
![]() где
- скорость движения воды в трубопроводе
до закрытия задвижки.
где
- скорость движения воды в трубопроводе
до закрытия задвижки.
Если время закрытия задвижки больше фазы удара (t3>Т), такой удар называется непрямым. В этом случае дополнительное давление может быть определено по формуле:
![]() Результат действия
удара выражают также величиной повышения
напора H,
которая равна:
Результат действия
удара выражают также величиной повышения
напора H,
которая равна:
при
прямом ударе
![]()
при
непрямом
![]()
35. Гидравлическое моделирование.
Гидравлическое моделирование осуществляется на специальных стендах, включающих фрагменты основных рабочих элементов в натуральную величину. Гидравлическое моделирование основано на общих законах подобия механических систем. Два потока жидкости подобны между собой, если они подобны геометрически, а также, если для всех сходственных точек обоих потоков соблюдается условия подобия их кинематических и динамических характеристик. Гидравлическое моделирование обычно осуществляется с помощью бачков с водой. Постоянную времени (и скорость разгона) в бачке можно изменять, изменяя объем, например, бачка. Гидравлическое моделирование основано на подобии движения печных ( топочных) газов и жидкостей ( воздуха) и предусматривает главным образом постоянство критерия Рейнольдса в натуре и модели. Специфика гидравлического моделирования требует расчета концентрации имитирующего вредность раствора в модели в соответствии с задаваемой в натуре концентрацией газа. Тем не менее, практика показывает, что в ряде случаев соотношение концентрации газа и раствора задается произвольным. Техника гидравлического моделирования является чрезвычайно непростым делом. При гидравлическом моделировании выявляют закономерности, определяющие величину сопротивления и производительность аппарата для различных типов контактных устройств.
36. Критериальные уравнения.
После приведения уравнения Навье-Стокса к следующему виду они стали содержать следующие типы переменных: 1) безразмерные независимые переменные ; 2) безразмерные зависимые переменные ; 3) безразмерные критерии – комплексы, состоящие из величин заданных по условиям однозначности .
После приведения к безразмерному уравнению изменился характер уравнений. Уравнения приобрели обобщенный вид, т.к. одно и то же значение любого критерия может быть получено путем бесконечного варьирования входящих величин. Уравнения могут быть записаны в виде:
Критерии подобия могут быть двух видов: 1) состоящие из разноименных параметров; 2) имеющие периодический вид, т.к. представляют собой отношение одноименных параметров. Относительные переменные также могут быть двух видов: 1) отношение переменной к одноименной величине, заданной по условию однозначности; 2) если по условию однозначности нельзя задать одноименную величину, то строится комплекс приводящий величину к безразмерному виду – число подобия;
В числа подобия входит определяемая величина. Критерий подобия состоит из заранее известных величин, заданных по условиям однозначности.
1) Критерий Рейнольдса - определяет соотношение сил инерции и вязкости в однородном потоке. Это важнейший гидродинамический критерий для вынужденного движения. При движении потока в нем возникают возмущения, которые исходят от стенок канала или вносятся в поток извне. Влияние возмущений зависит от соотношения сил. Если преобладают силы вязкости возмущения гаснут и поток не меняет своей структуры. Если преобладают силы инерции возмущения развиваются дальше, поток меняет течение, изменяется его структура. Граница соотношения сил определяется по значению Reкр. Если Re<Reкр преобладают вязкие силы, Re>Reкр – силы инерции. Re характеризует движение при соизмеримости инерции и вязкости. Если в потоке преобладает какой-то один вид сил характер перестает зависеть от величины Re. В этом случае говорят, что течение автомодельно относительно критерия Re.
2) Критерий гидродинамической гомохронности - определяет соотношение между периодом темпа внешних воздействий на поток и периодом перестройки скоростного поля. Используют только для нестационарных задач. - время, за которое проходит частица, движущаяся со скоростью V0, путь l0.
3) Критерий Фруда - определяет соотношение между силами инерции и тяжести в потоке. Используется только в задачах, в которых гравитационные эффекты имеют важное значение. Однако в таких задачах часто сложно задать характерную скорость (при естественной конвекции), поэтому строится критерий, в котором исключается скорость.
37. Гидравлические машины.
Гидравлические машины (гидромаши́ны) — одна из групп гидравлических механизмов. Термин «гидравлические машины» часто используют как обобщающий для насосов и гидродвигателей. Желательность такого обобщения вытекает из свойства обратимости насосов и гидродвигателей. Это свойство заключается в том, что гидравлическая машина может работать как в качестве насоса (генератора гидравлической энергии), так и в качестве гидродвигателя. Однако, в отличие от электрических машин, обратимость гидравлических машин не является полной: для реализации обратимости необходимо внесение изменений в конструкцию машины, и кроме того, не каждый насос может работать в качестве гидродвигателя, и не каждый гидродвигатель может работать в режиме насоса. Номинальная мощность, отдаваемая насосом в гидросистему или потребляемая гидродвигателем из гидросистемы, может быть определена по формуле:
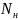 =
=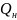 *
*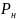 где
— номинальная подача насоса (для
гидродвигателя — номинальный расход
рабочей жидкости),
где
— номинальная подача насоса (для
гидродвигателя — номинальный расход
рабочей жидкости),
— номинальное давление на выходе из насоса (для гидродвигателя — номинальное давление рабочей жидкости на входе в гидродвигатель). Термин «гидравлические машины» не следует путать с термином «гидрофицированные машины». Под последними обычно понимаются машины, привод рабочих органов которых выполнен на базе гидравлического привода. Гидравлические машины являются необходимой частью гидропривода.
38. Центробежные насосы.
Центробежный насос — насос, в котором движение жидкости и необходимый напор создаются за счёт центробежной силы, возникающей при воздействии лопастей рабочего колеса на жидкость. Внутри корпуса насоса, который имеет, как правило, спиральную форму, на валу жестко закреплено рабочее колесо. Оно, как правило, состоит из заднего и переднего дисков, между которыми установлены лопасти. Они отогнуты от радиального направления в противоположную сторону, направления вращения рабочего колеса. С помощью патрубков корпус насоса соединяется с всасывающим и напорным трубопроводами. Если корпус насоса полностью наполнен жидкостью из всасывающего трубопровода, то при придании вращения рабочему колесу (например, при помощи электродвигателя) жидкость, которая находится в каналах рабочего колеса (между его лопастями), под действием центробежной силы будет отбрасываться от центра колеса к периферии. Это приведёт к тому, что в центральной части колеса создастся разрежение, а на периферии повысится давление. А если повышатся давление, то жидкость из насоса начнёт поступать в напорный трубопровод. Вследствие этого внутри корпуса насоса образуется разряжение, под действием которого жидкость одновременно начнёт поступать в насос из всасывающего трубопровода. Таким образом, происходит непрерывная подача жидкости центробежным насосом из всасывающего в напорный трубопровод. Центробежные насосы бывают не только одноступенчатыми (с одним рабочим колесом), но и многоступенчатыми (с несколькими рабочими колесами). При этом принцип их действия во всех случаях остается таким же, как и всегда. Жидкость будет перемещаться под действием центробежной силы, которая развивается за счёт вращающегося рабочего колеса. Центробежные насосы классифицируют по: Количеству ступеней (колёс); одноступенчатые насосы могут быть с консольным расположением вала — консольные; По расположению оси колёс в пространстве (горизонтальный, вертикальный); Давлению (низкого давления — до 0,2 МПа, среднего — от 0,2 до 0,6 МПа, высокого давления — более 0,6 МПа); Способу подвода жидкости к рабочему колесу (с односторонним или двухсторонним входом — двойного всасывания); Способу разъёма корпуса (с горизонтальным или вертикальным разъёмом); Способу отвода жидкости из рабочего колеса в канал корпуса (спиральный и лопаточный). В спиральных насосах жидкость отводится сразу в спиральный канал; в лопаточных жидкость сначала проходит через специальное устройство — направляющий аппарат (неподвижное колесо с лопатками); Коэффициенту быстроходности ns (тихоходные, нормальные, быстроходные); Функциональному назначению (водопроводные, канализационные,пожарные, химические, щелочные, нефтяные, землесосные и т. д.); Способу соединения с двигателем: приводные (с редуктором или со шкивом) или соединения с электродвигателем с помощью муфт.
КПД насоса зависит от коэффициента быстроходности ns, режима работы, конструктивного исполнения. При оптимальном режиме работы КПД крупных насосов может достигать 0,92, а малых около 0,6-0,75.
39. Основные показатели работы насосов.
Подача насоса (установки) — это количество жидкости перекачиваемой насосом (установкой) в единицу времени. Различают объемную подачу, массовую подачу и весовую подачу. В характеристиках насосов обычно принято задавать объемную подачу, т. е. объем жидкости, полезно используемый потребителем, при давлении, измеренном на выходе из насоса. Для гидроструйных насосов кроме полезной (пассивной) подачи должен быть задан расход рабочей (активной) жидкости. Напором насоса называют разность удельных механических энергий жидкости на выходе из насоса и на входе в него. Различают объемный, массовый и весовой напоры. Весовой напор имеет смысл в условиях определенного и постоянного поля гравитации. Он увеличивается с уменьшением ускорения свободнбго падения, а в условиях невесомости становится равным бесконечности. Поэтому весовой напор, широко используемый в настоящее время (на территории СССР он колеблется за счет изменения гравитационных сил в пределах 0,35 %, а в целом на Земле — в пределах 0,6 %), неудобен для характеристик насосов летательных и космических объектов. На практике очень часто для высоконапорных насосов скоростным напором и энергией положения пренебрегают вследствие их малости по сравнению со статическим давлением. Полная мощность насоса N расходуется на приведение его в действие. Она подводится извне в виде энергии приводного двигателя или с расходом рабочей жидкости, подаваемой к струйному аппарату под определенным напором. Коэффициент полезного действия (КПД) насоса — отношение полезной гидравлической мощности, к полной подводимой мощности. К показателям кавитации относят надкавитационный напор (кавитационный запас) — избыток удельной энергии жидкости над удельной энергией (упругостью) ее насыщенных паров. Для разных стадий развития кавитации различают следующие надкавитационные напоры: подавляющий — значение надкавитационного напора, при котором в насосе не проявляется никаких признаков кавитации; эрозионный (парогазовый) — значение надкавитационного напора, при котором обнаруживается эрозионное воздействие жидкости на проточную часть насоса; начало эрозии обнаруживается методом лаковых покрытий или путем анализа виброзвуковых характеристик; параметрический — значение надкавитационного напора, при котором появляются устойчивые кавитационные каверны; при испытаниях насосов рекомендуется принимать величину, при которой напор насоса уменьшается на 2 % по сравнению с бескавитационной работой при неизменной (заданной) подаче; предельный — наименьшее значение надкавитационного напора, при котором еще сохраняется кинематическое подобие (подобие течений) в модельном и испытываемом (натурном) насосах. Перечисленные кавитационные показатели являются объективными, однако для насосов важно знать необходимый надкавитационный напор. Этот параметр должен быть обеспечен в процессе эксплуатации для того, чтобы насос работал без существенного снижения напора и КПД или чтобы была ограничена приемлемыми пределами скорость кавитационной эрозии деталей насоса либо какие-нибудь другие показатели.
К показателям самовсасывания относятся следующие: Номинальная высота самовсасывания — расстояние по вертикали от свободной поверхности жидкости до верхней точки области возникновения кавитационных явлений, при которой насос обеспечивает самовсасывание жидкости определенного вида и последующую нормальную работу при температуре 20 °С и атмосферном давлении (0,1013 МПа). Подача воздуха при номинальной высоте самовсасывания — объемный расход (подача) воздуха, приведенный к давлению на входе в насос при отсутствии противодавления на выходе из насоса, атмосферном давлении 0,1013 МПа и температуре воздуха 20 °С. Показатель применим только для насосов со стабильной во времени характеристикой самовсасывания. Изменение подачи воздуха при самовсасывании во времени (нестабильность характеристики) определяется в основном нагревом жидкости, что хактерно для рециркуляционных систем самовсасывания. Минимальное время самовсасывания — время, в течение которого насос, работающий при номинальной высоте самовсасывания и отсутствии противодавления на выходе и имеющий подводящий трубопровод заданных диаметра и длины, осуществляет самовсасывание. Допустимая продолжительность самовсасывания — время, в течение которого допускается работа самовсасывающего насоса при номинальной высоте в режиме самовсасывания. При отсутствии режимных ограничений время обычно принимается равным времени, в течение которого подача воздуха уменьется на 25 % (например, вследствие нагрева жидкости для рециркуляционных установок и насосов).
К эргономическим показателям насосов и установок относятся следующие:
внешняя утечка, т. е. расход жидкости, вытекающий из насоса в наружную среду (например, через сальники) при номинальном режиме и определенном (заданном) давлении на входе;
уровень звукового давления — общий уровень звукового давления в дБ при пороговом значении, измеренном на расстоянии 1 м от наружного контура насоса (установки) в заданных точках при номинальном режиме работы насоса (установки);
уровень вибрации — общий уровень вибрации в дБ по эффективному (среднеквадратическому) значению колебательной скорости или ускорения, измеренный на опорной поверхности насоса (установки) в направлении, перпендикулярном к ней, в точках, где вибрация максимальна.
Для некоторых насосов (установок) применяют ряд специальных параметрических показателей — таких как допустимая продолжительность работы при нулевой подаче (при закрытой напорной задвижке) и т. п.
При выборе показателей надежности (наработка на отказ, ресурс, вероятность безотказной работы и т. п.) необходимо установить эксплуатационные допуски на рабочие параметры, так как чем больше допуск, тем выше надежность насоса.
Подобие насосов. Определить формы движения жидкости в насосах теоретическим путем на современной стадии развития науки не всегда представляется возможным. Поэтому в практике проектирования лопастных и струйных насосов во многих случаях используют опытные данные. Научно обоснованное обобщение результатов экспериментов можно выполнить с помощью методов теории подобия. Подобными называются явления, у которых все характеризующие их величины находятся между собой в постоянных соотношениях. Таким образом, при подобии потоков жидкости в насосах по известным характеристикам потока жидкости в одном из них (модели) можно получить характеристики потока жидкости в другом (натурном) насосе простым пересчетом. Такой переход аналогичен переходу от одной системы единиц физических величин к другой. Для обеспечения возможности такого перехода от модельного образца к натурному необходимо соблюдение геометрического, кинематического и силового (гидродинамического) подобия. Геометрическое подобие границ потоков (проточных полостей насосов) — необходимое условие подобия самих насосов. При соблюдении этого условия все сходственные линейные размеры проточной части сравниваемых насосов должны находиться в постоянном соотношении. Геометрическое подобие, кроме того, включает подобие относительных шероховатостей стенок проточной части насосов, толщин обтекаемых профилей.
Кинематическое подобие — это подобие траекторий движения частиц жидкости и равенство скоростей в сходственных точках потока (т. е. планы скоростей модельного и натурного потоков должны быть подобны). Силовое (гидродинамическое) подобие означает полное подобие потоков и характеризуется равенством отношений сил одинаковой физической природы, действующих на частицы жидкости или на границы потока, в сходственных точках. Силовое подобие в насосах возможно только при кинематическом подобии.
Характеристики насосов, используемые в практике. Размерные гидравлические характеристики насосов — это взаимозависимости основных параметров насосов (расхода, напора, надкавитационного напора, мощности, а для центробежных насосов и частоты вращения) и зависимости этих параметров от плотности жидкости, вязкости. Если все параметры переменны, то общую характеристику необходимо строить в многомерном пространстве. Такую характеристику невозможно изобразить графически и даже трудно себе представить. Поэтому приходится вводить определенные комплексы, составленные из указанных величин, принимая некоторые из них постоянными. Относительные характеристики — это такие, в которых за единицу величины характеризуемых параметров принимают определенные значения этих параметров, например напор, расход, мощность и КПД, соответствующие оптимальному режиму (режиму максимального КПД). Безразмерные характеристики выражают зависимости одной безразмерной комбинации параметров насоса от другой. Безмерные характеристики могут быть распространены на весь безразмерный (подобный) ряд насосов, характеризуемых, например, геометрическим масштабным коэффициентом. С этой точки зрения они очень удобны. Однако при использовании безразмерных характеристик необходимо учитывать возможность нарушения условий кинематического и динамического подобия, например вследствие возникновения кавитации или извлияния вязкости и других факторов.
40 Уравнение Эйлера в гидромеханике — дифференциальные уравнения движения идеальной жидкости в переменных Эйлера. Если давление р, плотность ρ, проекции скоростей частиц жидкости u, υ, ω и проекции действующей объёмной силы X, У, Z рассматривать как функции координат x, у, zточек пространства и времени t (переменные Эйлера), то Э. у. в проекциях на прямоугольные декартовы оси координат будут:
![]()
![]()
![]()
Решение общей задачи гидромеханики в переменных Эйлера сводится к тому, чтобы, зная X, У, Z, а также начальные и граничные условия, определить u, υ, ω, р, ρ, как функции х, у, z и t. Для этого к Э. у. присоединяют уравнение неразрывности в переменных Эйлера
![]()
В случае баротропной жидкости, у которой плотность зависит только от давления, 5-м уравнением будет уравнение состояния ρ = φ (р) (или ρ — const, когда жидкость несжимаема).
41 Теория подобия центробежных насосов
Прежде всего, расход определяется скоростью движения жидкости или просто скоростью движения кромки лопасти и площадью живого сечения рабочего колеса. Скорость численно равна произведению угловой скорости на радиус W = * R. Площадь живого сечения (площадь сечения для прохода жидкости) – геометрическая характеристика колеса и не зависит от числа оборотов. Радиус лопаток также не изменяется. Следовательно мы получаем зависимость: , где n – число оборотов вала насоса.
Иначе эта зависимость может быть записана следующим образом:
Q / Q1 = n / n1
Где n и n1 – новое и исходное числа оборотов соответственно;
Q и Q1 – новый и исходный расходы (при старом числе оборотов).
Аналогичные рассуждения можно привести для напора. Для этого необходимо вспомнить, что создаваемый напор определяется кинетической энергией жидкости. Кинетическая энергия в свою очередь пропорциональна квадрату скорости, а значит: H n2.
Н / Н1 = n2 / n12
Учитывая, что полезная мощность рассчитывается как N = * Q * H, получим
N / N1 = (Q * H) / (Q1 * H1) =n3 / n13
Замечание.
Обратите пожалуйста внимание, что при изменении числа оборотов изменяется и расход и напор. Парабола подобия может быть построена при необходимости по простой зависимости:
Н / Н1 = n2 / n12 = Q2 / Q12
Преобразуя получим: Н = (Н1 / Q12) * Q2
43 Работа насоса на сеть |
Совокупность насоса, приемного и напорного резервуаров, трубопроводов, связывающих вышеперечисленные элементы, регулирующей и запорной арматуры, а также контрольно-измерительной аппаратуры составляет насосную установку. Для перемещения жидкости по трубопроводам из приемного резервуара в напорный необходимо затрачивать энергию на: подъем жидкости на высоту Hг, равную разности уровней в резервуарах (эту величину называют геометрическим напором насосной установки); преодоление разности давлений в них pп и pн; преодоление суммарных гидравлических потерь hп во всасывающем и напорном трубопроводах. Таким образом, энергия, необходимая для перемещения единицы веса жидкости из приемного резервуара в напорный по трубопроводам, или потребный напор установки определяется по выражению:
Характеристикой насосной установки называют зависимость потребного напора от расхода жидкости. Геометрический напор Hг, давления pп и pн от расхода не зависят. Гидравлические потери являются функцией расхода и зависят от режима движения. При ламинарном режиме характеристика трубопровода изображается прямой линией, при турбулентном движении в шероховатых трубах потери напора, а следовательно и характеристика имеет вид параболы. |
44 Совместное подключения насосов в одной сети используют в тех случаях, когда нужно существенно увеличить производительность насосной установки или повысить напор.
Возможные варианты параллельного и последовательного соединения насосов. В первом варианте увеличивается подача жидкости при почти неизменном напоре, во втором - напор потока при неизменной подаче. Параллельная работа насосов возможна при одинаковых напорах насосов в каждый данный момент. Схема параллельного соединения двух различных насосов, их характеристики hн = f (Q) (кривые I и II), а также характеристика насосной установки Hпотр = f (Q). Для получения рабочей точки необходимо построить суммарную характеристику этих насосов Н? = f (Q) (кривую I + II), для чего составляют абсциссы (подачи Q) точек кривых I и II при одинаковых ординатах (напорах НН). Точка А пересечения кривых Hпотр = f (Q) и I + II будет рабочей точкой. Абсцисса точки А определяет суммарную подачу обоих насосов, ордината ее - напор, который развивают насосы:. Горизонтальная прямая, проведенная через точку А, пересекает характеристики обоих насосов точках В и С, которые являются рабочими точками насосов I и II.
Параллельное включение насосов оправдывает себя экономически, только если характеристика насосной установки Hпотр. = F (Q) является пологой кривой. Последовательная работа применяется в тех случаях, когда один насос не может обеспечить нужного напора. При этом подача насосов одинакова, а общий напор равен сумме напоров обоих насосов при одной и той же подаче.
45 Регулирование подачи и напора насоса В процессе наладки и эксплуатации насосной установки в зависимости от конкретных условий часто необходимо изменять подачу и напор насоса. Обеспечить работу насоса с заданной подачей (в пределах его характеристики) можно дросселированием или рециркуляцией жидкости, изменением числа оборотов рабочего колеса, изменением диаметра трубопровода и уменьшением диаметра рабочего колеса. В каждом конкретном случае возможно применение одного из перечисленных способов или их комбинации. Дросселирование представляет собой гашение напора за счет прохождения жидкости (газа) через уменьшенное сечение. Дросселирующим устройством может служить задвижка (кран, вентиль) или специальная шайба. Применяются также дроссельные втулки. Для дросселирования используют задвижку только на напорном трубопроводе насоса, но не на всасывающем. Дросселирование всасывающей задвижкой увеличит сопротивление линии всасывания и может вывести насос на режим кавитации. Регулирование подачи задвижкой удобно тем, что с ее помощью можно быстро изменить режим работы насоса в зависимости от обстоятельств, т. е. если насос работает в переменном режиме. В то же время, если требуется какая-то определенная подача, то после остановки насос необходимо снова регулировать, выводя его на заданный режим работы. В этом случае следует применять дроссельную шайбу, которая обеспечит постоянный перепад давления (при постоянном расходе). Дроссельную шайбу устанавливают между двумя фланцами на напорном трубопроводе. Диаметр отверстия шайбы определяют по формуле
При дросселировании перекачиваемой жидкости снижается к. п. д. насоса, так как часть мощности двигателя расходуется непроизводительно. Мощность, затраченная на дросселирование, тем выше, чем больше разность давлений до и после дросселирующего устройства. Она выражается формулой
Поэтому, если к дросселированию приходится прибегать постоянно и значение ∆р велико, то следует заменить насос или применить другой способ регулирования подачи. Рециркуляцией уменьшают подачу насоса за счет возврата части перекачиваемой жидкости из напорного трубопровода во всасывающий. Для этой цели в насосной установке предусматривают рециркуляционный трубопровод с регулирующим органом. Как и дросселирование, рециркуляция уменьшает к. п. д. насосной установки. Следует отметить, что у насосов с круто падающей характеристикой падение к. п. д. при рециркуляции незначительно. Примером могут служить вихревой и центробежно-вихревой насосы, у которых при незначительном повышении подачи резко снижается напор и уменьшается потребляемая мощность, т. е. кривая Q — Н круто идет вниз. Потребляемая мощность у этих насосов с повышением давления растет быстрее, чем у насосов с пологой характеристикой. Поэтому подачу насосов с круто падающей характеристикой выгоднее регулировать рециркуляцией. Уменьшить подачу и напор насоса можно также за счет уменьшения диаметра рабочего колеса, т. е. обточки его на токарном станке. Для этого колесо устанавливают на оправке в центрах и протачивают его по наружному диаметру до расчетного размера. Искомый диаметр колеса можно с достаточной для практических целей точностью определить из зависимостей
|
