8.5. Обжим

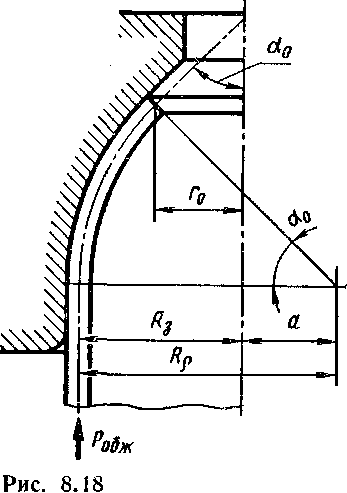
Анализ распределения напряжений в заготовке при обжиме приведен в работах [1, 33, 113]. Рассмотрим обжим цилиндри­ческой тонкостенной заготовки матрицей, образующая рабочей полости которой имеет постоянный радиус кривизны. На рис. 8.18 представлены схема деформирования заготовки в такой матрице и принятые обозначения размеров.

COS ОС,

Очаг деформации состоит из одного участка с постоянным радиусом кривизны срединной поверхности заготовки R_p — в ме­ридиональном сечении. В процессе деформирования заготовки край ее получает уменьшение радиуса г₀ от r₀ = R₃ в начале деформирования до заданного г₀. В соответствии с этим угол ос₀ между касательной к срединной поверхности в меридиональ­ном сечении на крае заготовки и осью симметрии увеличивается от ос₀ = О до значения, которое может быть выражено через R₃, а и г„ достаточно очевидным соотношением

о

- ' г₀ _ а + г₀ _ _{(8 99)}

Одновременно с этим в процессе деформирования заготовки радиус р любого ее элемента вследствие перемещения относи­тельно рабочей поверхности матрицы уменьшается, т. е. танген­циальная деформация элемента является деформацией сжатия.

Так как заготовка в процессе деформирования заталкивается в матрицу силой Р_обж, то в стенках исходной заготовки возни­кают сжимающие напряжения а_р, которые в очаге деформации по мере уменьшения радиуса р рассматриваемого элемента умень­шаются до нуля на крае заготовки при р = г₀. Учитывая то, что напряжения а_р являются сжимающими, а тангенциальная де­формация е₀ является деформацией сжатия, можно заключить, что напряжения а₉ также являются сжимающими.

Как было отмечено ранее, при R

(8.100)

значениях-^- > 10 напряженное со­стояние в очаге деформации с доста­точной точностью может быть при­нято плоским. Поэтому, учитывая, что напряжение а_р в очаге деформа­ции изменяется от нуля до некото­рого наибольшего значения а_ршах, можно заключить, что крайними глав­ными нормальными напряжениями бу­дут а₀ и а_н, причем а_и я» 0. Условие пластичности по постоянству макси­мального касательного напряжения (5.22) для этого случая имеет вид

0п = —о\

Распределение напряжений о_р в очаге деформации при об­жиме в матрице с криволинейной образующей (R_p = const) может быть получено путем совместного решения уравнения рав­новесия (8.6) и уравнения (8.100).

Рассмотрим вначале решение без учета влияния упрочнения и изменения толщины заготовки в процессе деформирования на величину напряжений о_р, действующих в очаге деформации.

Для заданной формы очага деформации (R_p = const) спра­ведливы следующие очевидные соотношения: р = R_p cos а — а;

dp — —R_p sin ada; R_e = R_{p со}^_д . Подставляя их в уравне- ние (8.6) и решая его совместно с уравнением (8.100), после не- сложных преобразований получаем

da_p ( sin a \ sin a -\- jx cos a

da

/ sin a \ sin a -4- it cos a _n , _n,,

„{ т и I—a, ^r ,—- = 0. (8.101)

P V cos a — b ' / ^s cos a — b ^v '

В уравнении (8.101) принято, что b = -75—. Уравнение (8.101)

является линейным дифференциальным уравнением первого по­рядка, решение которого имеет следующий вид:

С + о J ^{sina +} ^^c°^sa е~1 (гоГ^Ь - ^д) ^da da ^{1 ь} J cos а — b

X

»J \cosa — ^ь '

_xeJ\cosa-b . (8.102)

Выполняя интегрирование функций, входящих в показатель степени, получаем

о =Гс4-о f sin a + М- cos « ,_{n (cosa}__b)+lia j_a 1 _e__{ln (cosа}_₆₎__дк _ p L J cos a — Ь j

C + o_sJ (sina-(-pcosa)e^daj—_sa__& .

Для значений коэффициента трения р, < 0,2 без большой погрешности можно экспоненциальные функции е^^а и е~^^а заменить первыми двумя членами разложения их в ряд. Произ­водя указанную замену, раскрывая скобки в подынтегральном выражении и пренебрегая слагаемым, содержащим множитель ц², получаем

Ор = [ С + о, j (sin а -f ц cos а + pa sin a) da] J_s~^_b , а после интегрирования получаем

о_р = {С -f- o_s [2р sin a— (1 + pa) cos a]} ¹ ~

cos a-

Произвольную постоянную интегрирования С находим из граничных условий, согласно которым при a = a₀ (на крае заго­товки) напряжение а_р = 0. Пользуясь этим граничным условием, определяем значение произвольной постоянной С:

С = —o_s [2р sin а₀ — (1 + И«о) ^{cos а}о 1.

и, наконец,

о_р — — a_s [(1 -f- pa) cos a — (1 -f- иа₀) cos a₀ +

+ 2_tx(sina₀—slna)l ^"Ц" • (8.103)

Формула (8.103) позволяет установить распределение напря­жений 0_р = / (а) в очаге деформации при обжиме в матрице с криволинейной образующей при R_p = const. Из формулы видно, что напряжение о_р = 0 при a = a_n (на крае изделия); увеличи­вается по мере уменьшения угла а и достигает наибольшего зна­чения о'р при a = 0 (на границе между очагом деформации и недеформируемой частью исходной заготовки).

Подставляя в формулу (8.103) значение a = 0, получаем формулу (8.104) для определения величины напряжения о_р,. действующего на границе очага деформации:-

a_p = rzЈ-[l — 0 +M^ao)cosa₀-f 2pslna₀]. (8.104)

В формуле (8.104) напряжение а'_р дано в функции угла а₀. Это же напряжение можно выразить в функции радиуса г₀, для чего в формуле (8.104) тригонометрические функции необходимо заменить следующими очевидными выражениями:

р

cosa₀= IT ⁰ ; sina₀= =-

Ар кр

a_n = arccos

Rp '

Подставляя эти выражения в формулу (8.104), а также учи- тывая, что Ь — = ^° ^³ , получаем «р «р

^__ц ^{*. + *р-*.} _arccos ^{г. + Яр-*.) . (8.105)}

A3 "р /

В тех случаях, когда угол а₀ сравнительно мал, а₀ < 40^е,-без большого ущерба для точности можно принять, чтоа₀ cos а₀ — = sin а₀, и тогда формула (8.104) получит более простой вид

о'р = — пгтгО—cosa₀-|- pislna₀). (8.106)

Эту же формулу с помощью приведенных ранее выражений, связывающих тригонометрические функции g радиусами R₃, R_p, г₀, можно написать аналогично формуле (8.105)

o_P = -o_s (\-JJL+-^-VRl-(r₀-l-R_P-R₃r). (8.107)

Напряжение о_ршах, действующее в станках обжимаемой за­готовки, следует определять с учетом того, что у элементов за­готовки при перемещении из недеформируемого участка в очаг деформации уменьшается радиус кривизны срединной поверх­ности в меридиональном сечении от бесконечности до величины /?_р. Таким образом, на входе в очаг деформации элементы заготовки получают изгиб, что должно оказывать влияние на величину на­пряжения о_ршах. В первом приближении можно принять, что изгиб элементов заготовки при их перемещении относительно матрицы обжима при резком изменении радиуса R_p вызовет уве­личение напряжения о_р на Дгг_р, величина которого приближенно определяется по формуле (8.52). Тогда напряжение о_ршах будет равно сумме напряжения о_р и приращения напряжения До_р.

Если величину а_р определить по формуле (8.107), то получим

а_рШах = ~а₆[1--^+^₇Т/^-(_/-о + ^р~^)²+₁^].

(8.108)

Если обозначить отношение -^-= т_об, то формулу (8.108) можно записать несколько иначе:

^{1 — т}₀₆ ^{+ р У 2 (1 - m}_o6^{) g - (1 - т}_об^{)3 + .}

(8.108а)

Из формулы (8.108а) следует, что при постоянном значении

s Rn

пт-ав ^{и с} увеличением отношения -~- слагаемое, учитывающее

влияние трения на о_ршах, увеличивается, а слагаемое, учитыва­ющее влияние изгиба, уменьшается. Отсюда можно заключить, что при малых значениях коэффициента трения (д. < 0,1) уве-

личение отношения ~- может привести к незначительному умень-

АЗ

шению отношения — ^шах-, в то время как при относительно больших значениях коэффициента трения (р > 0,2) увеличение приводит к увеличению отношения ^{gp тах}.

Лз ^>

Аналогичным образом можно получить расчетные формулы для случая обжима в конической матрице (рис. 8.19). Очаг де­формации в этом случае состоит из двух участков: /, в котором заготовка соприкасается с конической полостью матрицы, и

ж	г,
У/ к*

участка II свободного изгиба с ра­диусом R_p срединной поверхности, в котором заготовка не соприкасает­ся с матрицей.

р

cos а_к

Распределение напряжений в ос­новном, коническом, участке очага деформации можно установить, под­ставляя значение а_е = —а₅ из усло­вия пластичности в уравнение (8.6) и учитывая, что а = const = ос_к;

оо и Rp. =

^Р~^Г + °р + °» 0 + И ^ct§^a^ = °-

Интегрируя это дифференциаль­ное уравнение с разделимыми пере­менными, находим

°р= — Ml + |ictgcg +

Произвольную постоянную инте- Рис. 8.19 грирования С можно найти из гра- ничного условия, согласно которому при р = г₀ (на крае заго- товки) напряжение о_р = 0:

С = r₀a_s (1 + (Л ctg ocj.

Подставляя значение С в предыдущее уравнение, получаем формулу (8.109), которая позволяет установить распределение напряжений в коническом участке очага деформации:

a_e(l + Hctgo_K)(l--^-).

(8.109)

Напряжение о'_р, действующее в коническом участке очага деформации на границе его с участком свободного изгиба, можно получить из формулы (8.109) при подстановке в нее значения Р ^{= r}i (рис. 8.19):

^ ₌ _a,(l+nctgcg(l-l2-).

(8.110)

Распределение напряжений на участке // очага деформации находим, решая уравнение (8.6), в котором принято р. = 0 (кон­такт заготовки с инструментом отсутствует). Получающееся дифференциальное уравнение имеет вид

day 0_Р + a_s

dp

Интегрирование его дает уравнение

При переходе элементов заготовки в процессе ее деформиро­вания из участка // очага деформации в участок / радиус средин­ной поверхности в меридиональном сечении увеличивается от R_p до бесконечности (спрямление), а при переходе из недеформи-руемой части заготовки в очаг деформации уменьшается от бес­конечности до значения R_p (изгиб). Считая, что изгиб и спрямле­ние вызывают увеличение напряжения о_р на До_р, величина ко­торого определяется по формуле (8.52), заключаем, что в качестве граничного условия для участка // очага деформации можно при­нять, что при р = г_х о_р — о_р+ До_р.

Используя это граничное условие, находим

^{-Ф + М}₈^{«к)(1—^)} _{+ 1}^{1-]=-«,, + -£;}

отсюда произвольная постоянная интегрирования С = _0/1[ 1 - (1 + ц ctg eg (1 - ) - .

Подставляя значение С в уравнение для определения вели­чины Ор в участке // очага деформации, получаем

°p = -^-f-Hl+Hctga_K)(l-f)f + ]•

(8.111)

Значение напряжения Ор, действующего в участке // очага деформации на его границе с недеформируемой частью заготовки, определим по формуле (8.111) при подстановке в нее значения р = R₃. Для упрощения в третьем и четвертом слагаемом примем

o; = -o_s[l--^₊(l + pctga_K)(l--^) + ₁|-_r]. (8.112)

Напряжение о_ршах, действующее в стенках обжимаемой за­готовки, с учетом влияния изгиба определим как сумму напря­жения о_р и приращения напряжения До_р:

<w = ~ °> [ ¹ it + (¹ + и ctg о,) (1 - -g-) + - 2^- ] •

(8.113)

Для определения о_ртах по формуле (8.113) при обжиме в ко­нической матрице необходимо знать величину радиуса участка свободного изгиба. В первом приближении можно принять, что величина R_p в участке // очага деформации определяется по фор-

392 .

муле (8.40), как в случае, когда меридиональное напряжение сравнительно велико:

К , ^МТ" . (8.114)

4a_p(l-cosa_K)

Подставляя значение R_p из выражения (8.114) в (8.113),

получаем

1 —

-^•+(l + l*ctg«_B)(l—^-) +

+ -*-(!-COS од

(8.115)

Подставляя значение о_р из (8.110) в (8.115), после несложных преобразований получаем

°_ргак= -o_s[l --^ + (l + HCtga_K)(l--^-) (3-2cosa_K)].

(8.116)

Так как при обжиме радиусы г_х и R_b незначительно отлича­ются по величине один от другого, то без большого ущерба для точности формулу (8.116) можно записать в несколько ином виде

a_pmax = - °s (1 + И ctgaj ( 1 — (3 - 2cos а,). (8.1 17)

Формула (8.117) позволяет определить величину напряже­ния о_ртах, действующего в стенках заготовки при обжиме в ко­нической матрице.

Заметим, что этой формулой нельзя пользоваться для опреде­ления величины а_ршах при обжиме в конической матрице, когда обжатая часть заготовки выходит в цилиндрическое отверстие матрицы, так как в этом случае появится новый участок очага деформации (на скругленной кромке матрицы), на границах кото­рого элементы заготовки будут получать изгиб и спрямление [70].

Проведенный анализ обжима в конической матрице и в матрице с криволинейной образующей был выполнен без учета влияния упрочнения и изменения толщины заготовки в процессе деформи­рования на величину а_ртах. Учтем, хотя бы приближенно, влия­ние упрочнения на величину а_ршах при обжиме в конической матрице, принимая, что напряжение текучести a_s связано с отно­сительным сужением при испытании на растяжение линейной зависимостью, и учитывая, что при обжиме тангенциальная де­формация е_е = ^^{3 р} эквивалентна относительному сужению.

A3

Из формулы (1.13) получаем уравнение для определения вели­чины o_s:

а, .-о₁₀ + я(1--^-). (8.118)

1.4 l.il'i 393

Заменяя в дифференциальном уравнении для конического участка очага деформации напряжение текучести a_s его значе­нием из уравнения (8.118), получаем

р-|г + °р + (°*° +⁷⁷ ~⁷⁷ ж) V + •*= ^0:

это уравнение можно записать в несколько ином виде: *т_Р ар , («_Т, + Я-Л-|-)(1 + ^_е«_к) dp Р Р

Уравнение является линейным дифференциальным уравне­нием первого порядка, решение которого можно написать в виде

_{°р = -7Г - Ко + Щ (1 -f р ctgод + Я (1 -f pctgaK)} ^р

Произвольную постоянную интегрирования находим из гра­ничного условия, согласно которому при р = г₀; о_р = О

г²

с = г₀ (о₁₀ + Я) (1 + р ctg од - я (1 + р ctg од -г^-.

Подставляя значение С после преобразований, получаем

Op = -[o_T0 + /7(l-^.)](l + _[ictga_K)(l--a.). (8.119)

Подставляя в формулу (8.119) значение р = R₃ и учитывая влияние изгиба на входе в матрицу множителем (3—2 cos ос_к) аналогично тому, как это сделано в формуле (8.117), получаем значение о_ршах, действующего в стенках обжимаемой заготовки с учетом влияния упрочнения:

Оршах = — [Чо + ^-)](l + |*ctgaj X

X (l — -^)(3-2cosa_K). (8.120)

Легко убедиться, что множитель j^o_T0 + ^ 1 j явля- ется по существу средним арифметическим максимального и ми- нимального значений напряжения текучести в очаге деформа- ции. Действительно, минимальное значение напряжения теку- чести o_{s min} = 0_тО ^при е_е = ^³ ~ ^³ = 0^ и максимальное зна-

чение напряжения текучести o_{s шах} = о_т0 -(- Я ³ ^ ⁰ (на кромке

обжимаемой заготовки при р == /"₀). Среднее арифметическое этих двух значений

„ _ °"s min ~Ь Q"s шах . /7 /1 ^ro \

u_{s С}р — ₂ — 0_тО -Y ₂ \ ¹ R₃ ) '

Таким образом, влияние упрочнения на величину а_ршах, действующего в стенках обжимаемой заготовки, приближенно можно учесть заменой в установленных ранее формулах напря­жения текучести a_s средним для очага деформации напряжением текучести, определяемым в предположении справедливости ли­нейной зависимости напряжения текучести от относительного сужения.

Рассмотрим теперь, каким образом можно учесть влияние изменения толщины заготовки в процессе деформирования на величину напряжения а_ртах, действующего в стенках обжимае­мой заготовки. Рассмотрим прежде всего характер изменения толщины заготовки при обжиме. Соотношение между скоростями деформации в любой точке очага деформации в данный момент деформирования можно установить по известным значениям напряжений. Уравнение связи напряжений и скоростей дефор­маций для плоского напряженного состояния (о_н == 0) в приня­тых обозначениях можно написать

gp — ffe _ е_р — е₉ ⁰е ё_в — е„

Выражая скорость деформации в_р = / (е_е, е„) по условию постоянства объема е_р = —е_е — е„ и подставляя это значение е_р в полученное уравнение, после преобразований находим

⁰е е„-ё₈

Для конической части очага деформации напряжения о_р в функции координаты р (без учета упрочнения) выражаются формулой (8.109); а_е = —о_ь (по условию пластичности). Под­ставляя значения а_е и а_р в уравнение связи, после преобразова­ний получаем

l + (l+Hctga_K)(l--^-) .

е„= ) ^е_е. (8.121)

2-(l+nctga_K)(i--^j

Из формулы (8.121) видно, что скорости деформации е„ и е₀ имеют обратные знаки, а так как скорость деформации е_е отрицательна, то скорость деформации е_п положительна. Другими словами, при обжиме толщина заготовки в любой точке очага деформации увеличивается.

Если принять в первом приближении, что соотношение между величинами напряжений а_р и а_е для любого элемента заготовки остается постоянным на протяжении всего процесса деформи­рования, то формулу (8.121) при замене скоростей деформации на деформации можно использовать для определения конечной

395

толщины стенки в обжатой части очага деформации. Так как при обжиме деформации значительны, то более правильные значения будет давать формула (8.121), если в ней использовать не отно­сительные деформации, а логарифмические

б„

In — и б_я = In ■—.

sii ^а R₃

Выполняя эти замены, получаем

l + (I+Hciga_K) (l- -£-)

, 2-(l+nctga_K)(l~

-)

(8.122)

Эта формула позволяет определить значение конечной тол­щины в любой точке обжатой части заготовки, отстоящей на рас­стоянии р от оси симметрии.

Конечное значение толщины стенки по краю обжатой части заготовки (при р = г₀) определяется более простой формулой

(8.123)

Конечная толщина стенки в обжатой части заготовки имеет наибольшее значение вблизи края заготовки и убывает по мере увеличения радиуса р, достигая минимального значения (s = s_H)

при р = R₃

На рис. 8.20 приведе­ны графики изменения тол­щины s вдоль образующей конической, обжатой части заготовки, полученные ра­счетом по формуле (8.122) и в опытах. Сопоставле­ние графиков показывает, что формула (8.122) пра­вильно отражает характер изменения толщины заго­товки при обжиме и дает вполне удовлетворитель­ную точность расчетных значений. Некоторая раз­ница между эксперимен­тальными и расчетными графиками, очевидно, объ­ясняется тем, что расчет­ное значение толщины определялось без учета 23 р,мм _ВЛИЯНИя упрочнения и из­гиба, которые способст-

И 39 Рис. 8.20

396

г, мм

3,8

3,7

3,5

ЗА

3,3

з,г

3,1

						^0,67
Обжим ак= const=15°					> Г""	о п
			Г °У
		/ >	/ /у	о—о171' о	1=0,77
		/р	т0& =	0,82
		' s У о
Ра	■f / /
У//

3,8

33

31

37 35

вуют более интенсивному изменению толщины стенок заготовки при деформировании.

Приведенные графики показывают также, что без большой погрешности можно принять, что конечная толщина в обжатой части заготовки находится в линейной зависимости от радиуса р.

Выражение s — f (р) и изменения толщины ds в этом случае можно записать

s = s_H (Лр -f Л о); ds = s_HAdp. (8.124)

Дифференциальное уравнение равновесия (8.7) для обжима в конической матрице с учетом изменения толщины заготовки в очаге деформации после использования условия пластичности имеет вид

Р^Г + °р(¹ +-Ј|-) + Ml + Hctga_K) = 0. (8.125)

Подставляя значения s и ds из (8.124) в (8.125), после неслож­ных преобразований находим

^ + <.Д^+^л) + «.^1±^=-0. ,8.126,

Решение этого дифференциального уравнения первого порядка с использованием граничного условия при р = г₀, о_р = 0 при­водит к формуле

о_Р = - ± (1 + Р ctg од [ 1 + _ JJL ] . _(8Л27)

Наибольшее значение о_р — а_ртах получает при р = R₃ на переходе от очага деформации к недеформируемой части заготовки (без учета влияния изгиба):

Os /1 I i \ /1 , А г_а Аг_в — 2А₀ \

op _т„ = - - (I + р ctga_K) (l + _{ARs + Ao} - -fi _{ARa + Au} ) •

(8.128)

Используя формулы (8.122) и (8.123) для отыскания значе­ния s на границах очага деформации, находим, что при р = R₃

s = s_H и AR₃ + А о = I, а при р = r₀ s = s_H ]/ -у³- и Аг_а +

+ л₀ = ]/Ж.

Подставляя приведенные соотношения в формулу (8.128), а также определяя из них значения Л и Л₀, после некоторых преобразований находим

o_pmax^-^₍l ₊ pct_ga_K)(l-]/^:₊|/^-^).

(8.129) 397

Эта же формула может быть представлена в несколько ином виде:

a_pmax = --^(l + u.ctga_K) (l -Ь УЧг)" ^(8Л2-⁹-^а)

Из формулы (8.129а) можно заметить, что множитель ~ 1л + "^"Т²") ^по существу является отношением средней

для очага деформации толщины заготовки s_cp == -i- -f- s_u .

к ее исходной толщине s_H.

Таким образом, влияние изменения толщины заготовки в про­цессе деформирования при обжиме на величину напряжения о_ртах> действующего в стенках обжимаемой заготовки, можно приближенно учесть введением в расчетные формулы, получен-

ные без учета изменения толщины, множителя -?jr(l + ]/ -7^*)'

Учет влияния упрочнения и изменения толщины заготовки в про­цессе обжима на величину а_ртах позволяет установить расчет­ные формулы, отражающие влияние всех основных факторов.

Например, для обжима в конической матрице без образова- ния цилиндрического участка меньшего диаметра (см. рис. 8.19) такую расчетную формулу можно получить на основе формулы (8.120):

^{<w=- 4[>}_т0^{+4 (1 - + x}

X (1 +fxctga_K) (l — -j^ ) (3 - 2 cos oc_K). (8,130)

Формула (8.130) позволяет определить величину о_ршах ^е У^че_ том влияния трения, изгиба, упрочнения и увеличения толщины заготовки в процессе деформирования. Анализируя формулу (8.130), можно заметить, что напряжение о_ртах увеличивается

g уменьшением отношения —-, а также е увеличением коэффи­циента трения, экстраполированного предела текучести а_т0 и модуля упрочнения 77, а кроме того, зависит от угла конусности матрицы. Зависимость o_paax = f(a_K) имеет сложный характер. Действительно, с увеличением угла конусности матрицы а_х множитель, учитывающий влияние трения (1 + ц ^cxg ^au), умень­шается, в то время как множитель, учитывающий влияние изгиба (3 — 2 cos a_K), увеличивается.

На рис. 8.21 показаны типовые графики зависимости Р_обж = = / (а_к) для обжима в конической матрице \ Из графиков видно, что существуют оптимальные значения углов конусности матрицы,

при которых при прочих равных условиях (^jr-; I³! ^стю ^и ^)

кгс

гиоо

2000

напряжение o"p _ma,i имеет ми­нимальную величину. Из тех же графиков можно заметить, что значение оптимального угла конусности матрицы увеличивается с увеличением коэффициента трения.

1600

1200

600

Рис. 8.21

Аналогичным образом вве­дением соответствующих мно­жителей в полученные ранее расчетные формулы можно .учесть влияние упрочнения и увеличения толщины за­готовки в процессе деформи­рования при обжиме в мат­рице с криволинейной обра­зующей.

Рассмотрим еще некоторые задачи, связанные с анализом операции обжима. Интересное решение может быть получено при допущении о том, что изменение толщины при обжиме может быть принято аналогичным изменению толщины в случае линей- ной схемы сжатия (допущение, приемлемое при обжиме с малыми обжатиями или для краевой части очага деформации, в котором напряжения о_р сравнительно невелики).

В этом случае из формулы (8.122) следует, что s = s_H|/^r-^³-,

Vr

a ds

— dp. Подставим найденные значения s и ds

2р Vp

в уравнение (8.125), которое при этом преобразуется к виду

dp

+ -у- о_р + о, (1 + р ctga_K) = 0.

Интегрирование этого уравнения с использованием гранич­ного условия при р = г₀, о_р = 0 приводит к формуле

Сопоставление полученной формулы с формулой (8.109) пока­зывает, что изменение толщины заготовки при обжиме способ­ствует увеличению абсолютных значений меридионального сжи­мающего напряжения.

В действительности увеличение толщины заготовки при обжиме происходит более интенсивно, чем при допущении о равенстве меридиональной деформации и деформации изменения толщины (линейная схема), особенно в участках очага, где о_р сравнительно велико.