8.3. Вытяжка без утонения стенки

Вытяжка является одной из наиболее распространенных и изученных операций листовой штамповки. Процесс вытяжки рассмотрен в работах С. И. Губкина 112], И. А. Норицына [17, 58], Л. А. Шофмана [120], Г. Закса [24], Р. Хилла [113] и др.

Ниже с учетом имеющихся работ дано рассмотрение операции вытяжки цилиндрического стакана в первом и последующих переходах.

8.3.1. Вытяжка плоской заготовки (1-й переход)

При вытяжке плоской круглой заготовки (рис. 8.11) пласти­ческую деформацию получает часть заготовки (фланец), находя­щаяся на плоском торце матрицы и на ее скругленной кромке, а остальная часть заготовки деформируется упруго или получает небольшие пластические деформации.

Под действием пуансона средняя часть заготовки вдавливается в отверстие матрицы. Вследствие сплошности заготовки переме­щение средней части вызывает появление во фланце растягива­ющих напряжений о_р, действующих в радиальных направлениях. Одновременно возникают сжимающие напряжения о_е, действу­ющие в тангенциальных направлениях. Если принять, что дефор­мирование фланца происходит при отсутствии нормальных и ка­сательных напряжений на его поверхности, т. е. без прижима,

то напряженное состояние в оча- ге деформации будет плоским и деформирование фланца будет ана- логично деформированию круглой пластинки с круглым отверстием, по контуру которого приложе- ны растягивающие напряжения (вследствие осевой симметрии де- формирования касательные напря- жения т_р0 = 0, а напряжения о_р и о_е являются главными нор- мальными напряжениями). Таким образом, схема напряженного со- стояния во фланце близка к пло- Ркс. 8.П ской разноименной.

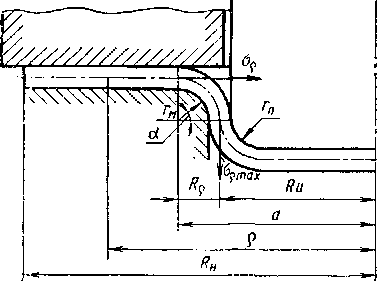
Донная часть заготовки (под торцом пуансона), которую можно рассматривать как круговую пластину, нагруженную радиаль­ными растягивающими напряжениями, также имеет схему пло­ского напряженного состояния, близкую к схеме двухосного растяжения.

В вертикальных стенках образующегося стакана напряженное состояние близко к линейному растяжению. Если внутренний диаметр стакана равен диаметру пуансона, то в стенках напряжен­ное состояние может быть близким к плоскому растяжению, а напряжения о_р и о_й являются растягивающими, причем о_е ^

?Ъ_

~ 2 '

Различие видов напряженного состояния в тех или иных участках заготовки создает возможность сосредоточения пласти­ческих деформаций во фланце заготовки. Действительно, по условию пластичности (5.22) пластическая деформация в стенках и донышке вытягиваемой заготовки может возникнуть в случае, если Op = o_s (линейная или плоская одноименная схема напря­женного состояния). В то же время фланец заготовки может де­формироваться при Op = o_s — | о₀ | < o_s. Таким образом, для успешной вытяжки необходимо, чтобы напряжение о_ртах, дей­ствующее на границе между фланцем и донной частью, не пре­восходило напряжение текучести. Отсюда следует, что основной задачей при рассмотрении процесса вытяжки должно быть отыска­ние величины о_ртах.

Решение этой задачи можно получить, установив зависимости, характеризующие закон распределения напряжений во фланце заготовки. Поле напряжений во фланце можно установить, исполь­зуя уравнения равновесия и пластичности. \Так как напряжения Ор и о_е имеют различный знак, то изменение толщины заготовки невелико (особенно в начальном периоде вытяжки). Отсюда сле­дует, что с достаточной точностью при отыскании поля напряжений во фланце можно использовать уравнение равновесия для оболочки постоянной толщины. В этом случае можно воспользоваться урав­нением равновесия для плоской задачи в полярной системе коор­динат (3.52) или, что то же, общим уравнением равновесия (8.6), в котором следует принять ц. = 0. Решение этого уравнения со­вместно с уравнением (5.22) (о_р — о_е = o_s), без учета влияния упрочнения, приводит к следующему уравнению:

= — o_s. (8.41)

^v dp

Интегрируя уравнение (8.41) и используя для отыскания про­извольной постоянной интегрирования граничное условие при р = R„, Ор = 0, получим

°_P = o_sln-^. (8.42)

Подставляя выражение для величины о-_р в условие пластич­ности, определяем величину напряжения о_е:

(8.43)

эти же формулы можно получить также методом характеристик (см. стр. 198).

Так как на переходе от фланца к донышку (при р = R_H) на­пряжение Ор при вытяжке не должно превышать напряжения текучести, то можно, пользуясь формулой (8.42), найти теорети-

ческую величину предельного коэффициента вытяжки k_B = = = —г-²-, определяемого как отношение диаметра заготовки к диа-

"и

метру вытягиваемого стакана. Подставляя в формулу (8.42)

р

о₀ = о , находим, что в этом случае In = 1, а предельный

коэффициент вытяжки k_{K пред} = 2,72.

Однако приведенный анализ распределения напряжений в очаге деформации не полностью отражает реальные условия деформа­ции заготовки при вытяжке. На распределение напряжений дополнительно оказывает влияние ряд факторов. В числе этих факторов основными являются трение под прижимом, трение на скругленной кромке матрицы, явления изгиба при переходе эле­ментов заготовки на скругленную кромку матрицы и при сходе с нее, упрочнение металла в процессе холодной деформации. Рассмотрим характер влияния каждого из указанных факторов.

При определенных соотношениях размеров заготовки и вы­тягиваемого стакана фланец заготовки под действием сжимающих напряжений может потерять устойчивость. Для предотвращения появления складок (гофров) фланец заготовки специальным устрой­ством (прижимом) прижимают к плоской части матрицы. В этом случае фланец заготовки со стороны прижима и матрицы будет подвергаться действию нормальных и касательных напряжений.

Величина касательного напряжения т_к пропорциональна нор­мальному напряжению

т_к = ц.о_н.

С тем чтобы установить вероятный характер распределения нормальных контактных напряжений по фланцу заготовки, рас­смотрим изменение толщины отдельных его элементов в процессе вытяжки.

Из уравнения связи напряжений и деформаций (5.24), учиты­вая, что при отсутствии прижима напряжения в направлениях^ нормальных к плоскости фланца, равны нулю, и заменяя индексы напряжений, получим

tfe _ 89 —е«

е_Р — е„ '

(8.44)

где е_п — относительная деформация по направлению толщины фланца.

Используя условие постоянства объема (е_р + е_е + г_п = 0), можно в уравнении (8.44) исключить деформацию е_р. Заменяя, кроме того, напряжения о_р и о_е их значениями, определяемыми формулами (8.42) и (8.43), находим

Ян

(8.45)

1 — 2 1п-

Р

2 —

Р

Из формулы (8.45) можно установить, что при 2 In —— <3 1

Р

(р > 0,607/?_н) деформация е„ имеет обратный знак по сравнению с деформацией е_е, а так как последняя является деформацией

R«

сжатия, то, следовательно, при указанных соотношениях деформация г_п является деформацией растяжения (толщина заготовки увеличивается). При 1п-^- = -2- (или, что то же,

при р = 0,607/?_н) деформация е„ = 0, а при 2 In -~- > 1 дефор-

Р

мация г_п становится деформацией сжатия, т. е. толщина заготовки в этой части фланца уменьшается.

Таким образом, краевая часть фланца в процессе вытяжки получает увеличение толщины, причем наиболее интенсивно это увеличение происходит вблизи края заготовки при р я» R_H,

где деформация е„ = ■—^-е₉.

Отсюда можно заключить, что усилие прижима при вытяжке будет распределяться по сравнительно узкой кольцевой части фланца, граничащей с наружным краем заготовки.

Обозначим усилие прижима Q, тогда суммарные силы трения, затрудняющие перемещение фланца к отверстию матрицы, будут равны 2p,Q (силы трения действуют между заготовкой и торцом матрицы, а также между заготовкой и прижимом). Заменяя при­ближенно действие сил трения на заготовку действием нормальных напряжений о_р, приложенных в радиальном направлении по кон­туру заготовки и равномерно распределенных по ее толщине, можно получить

Значение (т_р можно использовать в граничных условиях для определения произвольной постоянной после интегрирования уравнения (8.41). Принимая, что при р = R_u а_р — ст_р, получим

ъ = °*^1а-Т+-щ*'' <⁸-⁴⁷>

361

°в = -о.(1-Ш-^)+-^. (8.48)

Формулы (8.47) и (8.48) характеризуют распределение напря­жений в плоской части фланца при вытяжке с учетом влияния сил трения, вызванных действием прижима.

Если не учитывать влияния трения на кромке матрицы и влия­ния изгиба, происходящего в каждом элементе заготовки, кото­рый переходит с фланца на скругленную кромку матрицы и с по­следней в цилиндрическую часть образующегося стакана, то наи­большую величину растягивающего напряжения а'_р можно полу­чить из формулы (8.47) при подстановке в нее значения р = R„:

Однако при определении максимальной величины растягива­ющего меридионального напряжения пренебрегать действием изгиба и трения на кромке матрицы нельзя, так как они оказывают существенное влияние. Попытаемся приближенно учесть влияние этих факторов.

Рассмотрим вначале влияние изгиба и спрямления на величину растягивающего напряжения о_р. Каждый элемент фланца, пере­мещаясь в процессе вытяжки из плоской части на скругленную кромку матрицы, получает уменьшение радиуса кривизны средин­ной поверхности от оо до R_p. Такое резкое изменение радиуса кривизны срединной поверхности осуществляется действием про­дольных сил и моментов. Можно принять, что деформирование элементов заготовки, перемещающихся из плоской части фланца на скругленную кромку матрицы, аналогично деформированию полосы при изгибе с растяжением. Тогда величину момента, необходимого для изгиба, можно определить по формуле (8.33). Значение продольной силы (на единицу длины в тангенциальном направлении) находят как произведение напряжения о_р, опреде­ляемого по формуле (8.47) при р = а, на толщину s:

Как видно из формулы (8.33), увеличение силы N приводит к уменьшению величины изгибающего момента, однако эта фор­мула не учитывает влияния упрочнения при изгибе, которое спо­собствует увеличению изгибающего момента.

Для приближенных расчетов напряжения в опасном сечении можно принять, что величина изгибающего момента, действующего на переходе от плоской части фланца к скругленной, равна мо­менту, необходимому для пластического изгиба полосы без упроч­нения и при отсутствии продольных сил. В этом случае изгиба­ющий момент, отнесенный к единице длины в тангенциальном направлении, определяется из выражения (8.24). Возможность такого допущения была проверена экспериментально [69] путем 362

	7 \
	\
	i6r

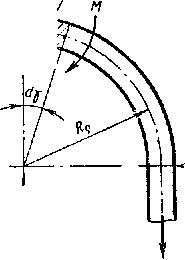о пределения величины угла подъема фланца при вытяжке без прижима под действием изгибающего момента, дейст­вующего в участке резкого изменения кривизны и приводящего к тому, что плоский фланец принимает воронкообраз­ную форму.

Рис. 8.12

Резкое изменение кривизны в мери­диональном направлении при изгибе и спрямлении требует затраты дополнитель­ной работы деформирования, которую можно приближенно учитывать условным увеличением продольных напряжений, не­обходимых для деформирования заготовки.

Величину приращения До_р, вызванного изгибом заготовки, можно найти из условия равенства работ, согласно которому работа изгибающего момента М на угле поворота сечения при изгибе должна быть равна работе силы, равной произведению До_р на площадь сечения заготовки на соответствующем пути переме­щения элемента заготовки.

В соответствии с обозначениями, приведенными на рис. 8.12, условие равенства работ при перемещении элемента заготовки из положения 1 в положение 2 (считая, что длина элемента в мери­диональном направлении не изменяется, так как учитывается только работа изгиба) напишем в виде

Ao_psR_p dy = •

dy,

(8.51)

откуда

Да_р = ^. (8.52)

Таким образом, можно считать, что изменение радиуса кри­визны в меридиональном направлении от бесконечности до опре­деленного радиуса R_p или, наоборот, от радиуса R_p до бесконеч­ности приводит к увеличению меридионального напряжения, дей­ствующего в участке изгиба или спрямления, на величину, опре­деляемую по формуле (8.52).

При вытяжке элементы заготовки, перемещаясь относительно матрицы, испытывают изгиб при входе на скругленную кромку матрицы и спрямление при сходе с нее. Влияние изгиба и спрям­ления на величину а_р было бы точнее учесть в граничных усло­виях раздельно для изгиба (при р = а) и спрямления (при р = = R_u), определяя величины напряжений раздельно для плоской и скругленной части фланца. Однако без большой погрешности можно принять, что влияние изгиба и спрямления на величину меридионального напряжения, действующего на переходе от скругленной части -фланца к цилиндрическим стенкам образую­щегося стакана, учитывается увеличением ст_р [по сравнению со значением, определенным по формуле (8.49) ] на удвоенное значение До_р, определенное по формуле (8.52).

Тогда величина напряжения о_р, действующая в опасном сече­нии и определенная без учета влияния трения на кромке матрицы, выразится формулой

Op = o_sln-f-₊₁^ + -i-o_s^-, (8.53)

в которой Яр = /•„ + -тг •

Влияние трения на кромке матрицы на величину напряжения, действующего в опасном сечении, более точно было бы определять на основе совместного решения уравнения равновесия выделенного в торообразном участке заготовки элемента, противостоящего скругленной кромке матрицы (относя силы трения к срединной поверхности), с условием пластичности. Такое решение было получено ранее [98 ], однако оно довольно сложное. В то же время, поскольку участок трения на кромке матрицы обычно мал по сравнению с размерами всего очага деформации, то и нет особого смысла стремиться к максимально точному учету влияния сил тре­ния на кромке матрицы. Приближенно влияние их можно учесть аналогично тому, как это сделано в известном решении Эйлера о трении ремня по шкиву. Таким путем влияние трения учитывали многие исследователи [12, 24, 120 и др.].

Как известно, по Эйлеру, увеличение напряжений вследствие действия сил трения учитывается введением множителя е^", где е — основание натуральных логарифмов; р, — коэффициент тре­ния и а — угол охвата шкива ремнем.

Приняв, что при вытяжке влияние трения на кромке матрицы можно учесть введением такого множителя, и считая, что угол

охвата а = -у (наибольшее растягивающее напряжение обычно

достигается после полного охвата заготовкой кромки матрицы), получаем

<W = ^ (1п-£ + "^7+ е^; (8.54)

эта формула позволяет определить наибольшую величину растя­гивающего напряжения в опасном сечении. Без большой погреш­ности, с целью дальнейшего упрощения формулы, можно при­нять, что

е^дТ^_{1 + [г}^_{1 + 1)6[г>} Тогда формула (8.54) примет вид

<W - о. + + *йт)<1 + 1.6|*). (8-55)

В формулу (8.55) входит усилие прижима Q, величину которого можно определить по приводимым в справочной литературе данным.

Кроме того, на основании обработки экспериментальных дан­ных некоторых исследователей можно предложить эмпирическую формулу (8.56), позволяющую определить минимальную величину усилия прижима, необходимого для предотвращения складкооб­разования при вытяжке цилиндрических стаканов:

Q = 0,1 (1 _ ^gi^y-gf-) ^_m„; (8.56)

в этой формуле D„₀ = ?.R_H0 — диаметр исходной заготовки; D R

k_B = —^- = —тг коэффициент вытяжки, определяемый как от-

ношение исходного диаметра (радиуса) заготовки к диаметру (ра­диусу) вытягиваемого стакана; Р_шах — наибольшее усилие вы­тяжки.

Формулой (8.56) можно воспользоваться для исключения ве­личины Q из формулы (8.55). В этом случае необходимо учесть, что

Ртах ⁼ 2ld_HSOp _шах.

Заменим в формуле (8.56) Р_тах приведенным соотношением и подставим полученное выражение для Q в формулу (8.55). Решая уравнение относительно cr_pmaX) после несложных преобра­зований находим

^а'(^]п1Г⁺ 2г 4 s )(' + ¹'⁶И)

_ \ к и ^'м ~Т" ^ь i /о С7\

°_ртах — ' 7 VoTZ Г {О.О/)

1 _0.2ц (1 + 1,6^(1-^-^-)*.

Формулы (8.55) и (8.57) позволяют определить значение на­пряжения о_{р тах}, действующего в опасном сечении заготовки при вытяжке цилиндрического стакана без учета влияния упрочнения, при сравнительно больших габаритных размерах изделия, когда

—— > 10. Последнее ограничение связано с тем, что при ширине

фланца, немного отличающейся от радиуса скругления кромки матрицы, уменьшение диаметра заготовки к моменту полного охвата ею кромки матрицы будет значительным, и в формулах (8.55) и (8.57) необходимо вместо начального диаметра заготовки подставлять значение диаметра, который получит заготовка к мо­менту завершения охвата кромки матрицы.

Эти формулы учитывают также влияние на величину о_ртах трения под прижимом и на скругленной кромке матрицы, изгиба и спрямления элементов заготовки при их перемещении относи­тельно матрицы. Формула (8.57) справедлива при оптимальном усилии прижима, величина которого определяется по формуле (8.56). Заметим, что по формуле (8.56) при определенных значе­ниях k_B и -j-,— усилие прижима равно нулю и даже может полу-

чить отрицательные значения. Это указывает на то, что при данных

значениях k_B и ■ ^s ■ прижим не нужен, и, следовательно, формула

(8.56) справедлива до значения Q = 0.

По формуле (8.56) Q .— 0 при D — d = 18s, что примерно соответствует соотношению, разграничивающему вытяжку с при­жимом и вытяжку без прижима, по Л. А. Шофману [121].

'В тех случаях, когда вытяжка идет без прижима, формулы (8.55) и (8.57) приводятся к виду

Smax=O_s(ln^+-2₇-^p_T)(l + 1,6р). (8.58)

Пользуясь формулами (8.55)—(8.57) для определения с_ртах, было бы более правильно в качестве R_H и £>_н0 подставлять не исходные значения радиуса или диаметра заготовки, а значения этих размеров в момент вытяжки, когда завершен охват заготов­кой скругленной кромки матрицы. В первом приближении это уточнение можно реализовать, используя условия постоянства толщины заготовки при вытяжке (или, что одно и то же, условия постоянства площади поверхности при вытяжке). Из условия

равенства площади поверхности исходного кружка

и площади заготовки в момент, когда завершен охват заготовкой скругленных кромок пуансона и матрицы, для случая, когда ра­диусы скругления пуансона и матрицы равны, получим

= ]АвО-2,3-^. (8.59)

Из формулы (8.59) видно, что при малых значениях ~- < 0,1

текущее значение коэффициента вытяжки k_BT мало отличается от

исходного значения k_B0 = ^D"^u , определяемого по диаметру ИСХОД­ЕН

ного недеформированного кружка D_h0. Однако в тех случаях, когда г_м относительно велик, формула (8.59) позволяет но исход­ным размерам заготовки и матрицы определить значение D„ — = 2R_K, которое следует подставить в формулы (8.55)—(8.57). В случае необходимости можно приближенно учесть влияние упрочнения на величину a_pmax, пользуясь формулами (1.13), (1.19) или (1.20). При вытяжке можно принять, что деформацией, эквивалентной по упрочняющему эффекту относительному суже­нию образца при растяжении, является относительная деформа­ция в тангенциальном направлении е₆.

366

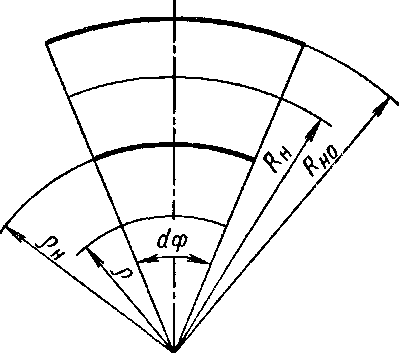
Величина тангенциальной де­формации при вытяжке e_fi яв­ляется функцией радиуса р. Ее можно найти для любого момента деформирования из условия по­стоянства толщины заготовки (по­стоянства площади поверхности заготовки). В процессе вытяжки радиус наружной кромки заго­товки уменьшается от исходного значения R_h0 до значения R_H в данный момент деформирования (рис. 8.13). В процессе деформи­рования исходный радиус любо- _{Рис 8}.13 го выделенного элемента также

уменьшается от исходного значения р_н до текущего значения р в данный момент деформирования.

Из условия постоянства площади поверхности заготовки при вытяжке следует, что

Яно^ф+Ри^ф (U r,\ ^R" ^d(f + P^d(f ID ~_V

2 v^ho — Рн) = 2 ⁴ ~~ P''

отсюда получаем

Pu=VR'U + pⁱ-Rl- (8.60)

Подставляя значения для р_н в формулу, определяющую отно­сительную деформацию в тангенциальном направлении, получаем

е_в=1--Н-=1 ^р (8.61)

Подставляя значение е_е вместо ф в формулу (1.13), (1.19) или (1.20) и заменяя значение o_s в уравнении (8.41) найденным выражением напряжения текучести в функции координаты р, можно найти распределение напряжений во фланце заготовки при заданном уменьшении его диаметра в процессе вытяжки с учетом влияния упрочнения.

Точное решение этой задачи связано с математическими труд­ностями и приводит к необходимости численного интегрирования [120]. В предыдущих изданиях учебника, а также в работе [70] даны некоторые варианты приближенных решений этой задачи с использованием различных аппроксимаций кривой упрочнения, Позволяющие получить решение в виде аналитических функций.

Ниже предлагается новый вариант решения, использующий степенную аппроксимацию кривой упрочнения (более точно отра­жающей характер изменения o_s = f (ф) по сравнению с линейной аппроксимацией) без осреднения значения напряжений текучести во фланце. С этой целью упростим формулу (8.61) с помощью раз-

367

ложения в ряд функции вида _г я« 1 %- -f -~ ...

V '1 + у ¹ °

и заменим функцию двумя первыми членами разложения в ряд.

#2 ^2

Такая замена не внесет большой погрешности, если —5__—2_<g i_t

и приемлема для рассмотрения начальной стадии вытяжки, когда °р max может достигать своего экстремального значения. В этом случае формула (8.61) преобразуется к виду

^н0 ^— R\ /о ci \

4 = ф • (8.61а)

Подставляя найденное значение е₉ = \\> в формулу (1.19) и заменяя в уравнении (8.41) значение a_s найденным выражением, получим

/ „2 г>2 \ ^г~% Р _dp - 1_я|,_ш \_ ₂гр_шР2 Интегрирование данного дифференциального уравнения с ис­пользованием граничного условия (р == R • а₀— ^ \ для

отыскания произвольной постоянной интегрирования приводит к формуле

\ 2^ш j \Р ^А" / ^ 7lR_Hs •

(8.62)

Максимальное значение а_р имеет место на входе в отверстие матрицы при р = R_H, а если обозначить X = то формула

для определения о_ртах может быть представлена в виде

²*„

2*.

^_ 2гр_ш ^ 2яь_ш j ц R_H )

(8.62а)

Как видно из формулы (8.62а), напряжение о_ртах равно нулю при X = 1 (в начале вытяжки) и при X = ^н° (в конце вытяжки).

Rh

Отсюда следует, что при промежуточных значениях радиуса фланца R_H < R_H < R_n0 должен иметь место экстремум напря­жения о_{р шах}. Величина Х_э, соответствующая экстремальному зна­чению Ор_Шах, может быть найдена из условия ^dg^^ax = 0. После

дифференцирования и некоторых преобразований формула для определения Х_э получает вид

^{Хз =} _(~жУ^ш_' ⁽⁸_-⁶³⁾

Из формулы (8.63) следует, что при вытяжке без упрочнения (ф_ш = 0) экстремальное значение а_ршах имеет место в начале вы­тяжки (при R_H = R_H0), а при вытяжке с упрочнением чем больше интенсивность упрочнения (чем больше ф_ш), тем большее умень­шение диаметра фланца заготовки соответствует возникновению экстремального значения напряжения а_ршах.

Экстремальное значение о_{р шах э} может быть найдено по фор­муле (8.62а) при подстановке в нее значения X = Х_э из формулы (8.63) (без учета влияния трения и изгиба на кромке матрицы). После некоторых преобразований конечная формула может быть представлена в виде

1

Здесь обозначено k_B = коэффициент вытяжки.

ЛИ

Влияние изгиба и трения на кромке матрицы может быть учтено аналогично тому, как это было сделано при выводе формулы (8.55). Если же, кроме того, принять, что в слагаемом, учитыва­ющем влияние изгиба и спрямления на кромке матрицы, можно принять, что o_s ^c„, а в слагаемом, учитывающем трение под прижимом, R_H = R_h0, то конечная формула (8.64) получает сравни­тельно простое написание

+

²Ф„

HQ

2tiu I ^ nR_HOsa_B ¹ 2r_M

(1 + 1,6ц). (8.64)

Формула (8.64) позволяет оценить влияние основных факторов на величину экстремального растягивающего напряжения, воз­никающего в опасном сечении (у донышка) при вытяжке.

Представляет интерес оценка влияния интенсивности упрочне­ния (характеризуемой величиной ф_ш), по которому до настоящего времени в научно-технической литературе нет достаточно опреде­ленного суждения.

Пренебрегая влиянием изгиба и трения и считая, что напряже­ние с_ртахэ < а_в обеспечивает условия вытяжки без разрушения заготовки, из формулы (8.64) может быть получено выражение для определения предельного коэффициента вытяжки в следующем виде:

1

> *впред=(¹+²Ч'ш)²*^Ш-

Из полученного выражения следует, что предельный коэффи­циент вытяжки монотонно, хотя и не резко, уменьшается с увели­чением ф_ш, т. е. с увеличением интенсивности упрочнения. Таким образом, с увеличением интенсивности упрочнения рост напряже-

ний в опасном сечении вследствие упрочнения перекрывает влия­ние уменьшения диаметра заготовки, которое к моменту возник­новения о_ршахэ также повышается с увеличением ijv

Заметим, что более точное изучение влияния интенсивности упрочнения на предельный коэффициент вытяжки могло бы быть выполнено при использовании аппроксимации кривой упрочнения функций вида (1.20), используя допущения, принятые при выводе формулы (8.64). Расчеты по формулам (8.62а) и (8.64) показывают, что упрочнение способствует увеличению растягивающего напря­жения, действующего в опасном сечении в течение всего процесса вытяжки по сравнению с вытяжкой без упрочнения.

Анализируя формулу (8.64), можно установить, что величина о_{ртах 9} возрастает с увеличением коэффициента трения и тем интен­сивнее, чем меньше относительная толщина заготовки = -~~. С уменьшением толщины заготовки увеличивается опасность по­тери устойчивости фланца заготовки, а силы трения, отнесенные к меньшей площади поперечного сечения заготовки 2nR_Hs, дают большее значение растягивающего напряжения, действующего по краю заготовки, а следовательно, и увеличивают напряже­ние о_ршахэ.

Из формулы (8.64) следует, что величина о_ртаХ9 при прочих равных условиях увеличивается по мере уменьшения радиуса скругления рабочей кромки матрицы при постоянной толщине заготовки. Характер зависимости о_ршах== / (~г~) иллюстри­руют приведенные на рис. 8.14 графики, полученные расчетом по

s 2s

= 1,8 и 1,9. Как

формуле (8.64) при и, — 0,1; -я- =*= -jr = 0,02; ijj =0,15 и на-чальных коэффициентах вытяжки k_B — ™

Rh

> 8, а особенно интенсивное увеличение наблюдается при

< 5, причем при —■ » 0

видно из графиков, увеличение о_ршахэ по мере уменьшения отно­шения -у- происходит сравнительно медленно при значении

Г м

;— «Ч^ и, нрпчсш HJJII -

(острая кромка матрицы)

на-

^г к S

превышает о_в, что указывает на невозможность осуществления вытяжки в этих условиях (за­готовка будет обрываться, и вытяжка по существу перехо­дит в пробивку). Характер функциональных зависимостей от основных

1,1

величины а,

р max э

1,0 0,9 0,6 0,7 факторов, устанавливаемый из формул (8.55) и (8.64), совпа­дает с характером тех же зависимостей, полученных экспери­ментально. Это свидетельствует о том, что принятые в анализе операции вытяжки допущения не искажают реальных функцио­нальных зависимостей, существующих в условиях вытяжки.

Пользуясь полученными формулами, можно попытаться уста­новить график изменения усилия вытяжки по пути пуансона, а также найти работу деформирования при вытяжке. Усилие вытяжки в любой момент деформирования, начиная с того момента, когда заготовка завершает охват скругленной кромки матрицы, можно определить ио соотношению

Р = 2uR_KSG_p [цах»

где а_{р тах} определяется при значении R_n, соответствующем дан­ному положению пуансона.

До опускания пуансона на величину, равную сумме радиусов скругления рабочих кромок пуансона и матрицы, когда заготовка еще не охватила полностью скругленные кромки пуансона и ма­трицы, а_ргаах на границе очага деформации наклонено под углом к оси пуансона, отличным от 0°.

На первом этапе вытяжки, когда величина рабочего хода пуан­сона изменяется от х = 0 до х = г_м + г_п 2г_м, усилие вытяжки возрастает от 0 до значения, определяемого по формуле (8.64), при R_H, полученном по формуле (8.59).

В тех случаях, когда г_ы и г_п малы по сравнению с размерами заготовки, наружный радиус заготовки в промежуточных стадиях деформирования из условия постоянства площади ее поверхности приближенно определяется формулой

R_u = VR%o — 2R*h, (8.65)

где h — текущая высота втянутой в матрицу части заготовки (рабочий ход пуансона).

Подставляя это значение R_H в формулу (8.62а), можно полу­чить зависимость, характеризующую изменение а_{р гаах} по пути пуансона, интегрируя которую найдем работу деформирования.

Для упрощения выкладок дадим решение без учета влияния упрочнения на напряжение текучести. Заметим, что решение с учетом влияния упрочнения в несколько ином варианте дано в работе А. Г. Овчинникова [60]. Используя формулы (8.55), (8.65), получаем формулу (8.66), характеризующую зависимость усилия вытяжки без упрочнения от пути пуансона при малых по сравнению с размерами заготовки значениях г_ы и г_п:

Р = 2nR_asa_s [ In VR^-^h ₊ ixQ _ ₊

^1<а nsos У Rio — 2R_Kh

+ -97-ТГТ (1 + 1,6ц). (8.66)

_ln VRlo-2R„h __ln R,

Логарифмическую функцию преобразуем по соотношению

Яи

1

In 1 —

ЯнО

1П

Яи

ЯнО Ян'*

Яи

ЯнО

+

С учетом данного преобразования находим работу деформиро­вания

н

Ruo R*h . hQ

Ян

ЯнО

А = 1 2nR_aso_s j ln

2R„h

+

2r_M + s Яи/l²

2ЯнО

(1 + 1,6ц,) dh = 2n^„sor_s (1 -f- l,6p,)

н

nso_s/<_H 2r_M + ^s

ft In

Я_но Я_и

Яи

Я_ИЯ 2ЯнО

+

_{2nRHHsas HQ}

+ 13& - У®* ~ 2R»H) + (1 + 1,6,.). (8.67)

При интегрировании было принято, что усилие прижима постоянно по ходу пуансона, что приближенно соответствует условиям вытяжки с пневматической подушкой.

Формулу (8.67) можно написать более просто, если конечную высоту Н вытянутого стакана выразить по условию постоянства площади поверхности заготовки через диаметральные размеры заготовки и вытянутого стакана:

И

ЯнО — Ян

2Яи

а также обозначить k_w =

Ян

Яи '

lr\k_B

+

+

А = nRl(kl~ l)sa, 2|xQ

nsR_H(k_B+ 1)ct_s ¹ 2r„ + s

+

ki — i

(i + 1,6ц).

(8.68)

Согласно формуле (8.68) работа вытяжки А = 0 при k_B — 1 и увеличивается с увеличением коэффициента вытяжки, коэффи­циента трения, усилия прижима, относительной толщины заго­товки и габаритных размеров вытягиваемого стакана. 372

В заключение рассмотрения первого перехода вытяжки дадим приближенное решение для вытяжки с подогревом фланца. Осо­бенность вытяжки с подогревом фланца состоит в том, что умень­шение величины напряжения текучести во фланце по сравне­нию с напряжением текучести в опасном сечении позволяет втя­гивать в матрицу без опасности разрушения (о_ршах < a'_s, где Os — напряжение текучести в опасном сечении заготовки) зна­чительно более широкий фланец (коэффициент вытяжки k_B —

■ — увеличивается). Однако равномерный нагрев фланца, при

Ли

котором величина напряжения текучести по всему фланцу будет постоянной, не может дать существенного увеличения коэффи­циента вытяжки. Действительно, в этом случае значения о„ =

= a_s; o_fl = 0 будут достигнуты во фланце при определяе-

мых из формулы (8.47), и опасное сечение переместится от кромки матрицы (где напряжение текучести при охлажденном пуансоне может быть выше, чем напряжение текучести во фланце) на плос­кую часть фланца, где начнется повышенное утонение с после­дующим разрывом заготовки. Поэтому для существенного уве­личения коэффициента вытяжки при подогреве фланца нужно создавать неравномерное температурное поле, при котором зна­чение напряжения текучести будет монотонно увеличиваться от наружного контура заготовки к рабочей кромке матрицы [10].

Предположим, что температурное поле таково, что зависимость напряжения текучести от координаты р определяется соотношением

а₈ = <-тг' (⁸-⁶⁹)

где a'_s — значение напряжения текучести у кромки матрицы.

Подставляя значение o_s из (8.69) в (8.41) и интегрируя полу­ченное дифференциальное уравнение с использованием гранич­ного условия при р = R_a; а_р = Jf®_s , получаем

Формула (8.70) характеризует распределение напряжения а_р во фланце при принятой зависимости напряжения текучести от координаты. Используя условия пластичности, легко получить формулу, характеризующую распределение напряжений сг_в во фланце. Максимальное значение а_р будет на границе между оча­гом деформации и стенками образующегося при вытяжке стакана при р = R_u. Учитывая влияние изгиба и трения на кромке мат­рицы аналогично тому, как это было сделано в предыдущих ре­шениях, можно получить формулу (8.71), позволяющую опреде­лить максимальную величину напряжения о_ршах в опасном се­чении с учетом трения под прижимом, изгиба и трения на кромке матрицы при принятой зависимости напряжения текучести от координаты:

^Jp max

Из формулы (8.71) можно видеть, что при заданном изменении напряжения текучести от координаты р предельный коэффициент вытяжки, определяемый из условия о_ршах = o'_s, значительно превышает коэффициент вытяжки при постоянном по фланцу значении напряжения текучести, и без учета влияния сил трения и изгиба этот коэффициент стремится к бесконечности. Проведен­ный анализ показывает, что созданием такого температурного поля во фланце вытягиваемой заготовки, при котором напряжение текучести убывает по мере удаления от рабочей кромки матрицы обратно пропорционально текущему, координирующему данную точку радиусу, коэффициент вытяжки может быть резко увеличен по сравнению со значениями, достижимыми при вытяжке без по­догрева фланца.

8.3.2. Вытяжка цилиндрической заготовки (последующие переходы)

Рассмотрим теперь последующий переход вытяжки, осуще­ствляемой в конической матрице. В этом случае деформируется полученная в предыдущем переходе заготовка в форме стакана, который в процессе деформирования умень­шается в диаметре.

Усилие вытяжки возрастает, пока рабо­чий торец пуансона не пройдет цилиндри­ческий поясок матрицы на расстояние, не­сколько превышающее величину радиуса скругления рабочей кромки пуансона, а потом остается примерно постоянным. Этому же моменту соответствует и наиболь­шая величина растягивающего напряжения Ор, действующего в зоне перехода от очага деформации к стенкам образующегося в про­цессе вытяжки стакана.

Очаг деформации в этом случае (рис. 8.15) можно разделить на три участка. Участок /, граничащий со стенками исходной заго- товки, в котором срединная поверхность за- готовки в меридиональном сечении имеет ра- диус R_p, а сама заготовка не соприкасается с поверхностями рабочего инструмента; уча- Рис. 8.15 сток //—заготовка соприкасается с кони- ческой частью, и участок /// — заготовка соприкасается со скругленной кромкой матрицы.

Рассмотрим распределение напряжений в каждом из участков очага деформации без учета изменения толщины заготовки и упрочнения.

Участок / имеет криволинейную образующую, и для этого участка справедливо уравнение равновесия (8.6), Однако так как в этом участке заготовка не соприкасается с поверхностями рабо­чего инструмента, то нормальные и касательные напряжения на поверхности заготовки отсутствуют. Для этого участка в уравне­нии (8.6) следует принять ц. = 0, и тогда по написанию оно становится аналогичным уравнению равновесия (3.52), а при ис­пользовании условия пластичности по постоянству максималь­ных касательных напряжений приводится к уравнению (8.41). Интегрируя полученное дифференциальное уравнение, находим

о_р = - or_s In р + С. (8.72)

Так как переход элементов заготовки из недеформируемон части заготовки с радиусом R₃ в очаг деформации сопровожда­ется уменьшением радиуса кривизны срединной поверхности от бесконечности до значения, равного R_p, то в качестве граничного условия можно принять условие, по которому при р = R₃ (на границе очага деформации) величина о_р должна быть равна Ло_р, т. е. приращению напряжения о_р, вызываемому изгибом элементов заготовки. Величина Аа_р определяется из выражения (8.52). Используя это граничное условие, находим

С = аЛп#₃ +

Подставляя это значение С в уравнение (8.72), получаем a_p = a_sln^ + -^. (8.73)

Формула (8.73) позволяет установить распределение напря­жений в участке / очага деформации.

Распределение напряжений в участке // (коническом) очага деформации можно определить также решением уравнения равно­весия совместно с условием пластичности.

В этом случае при R_p = оо я R_e = _cp^P_a уравнение равно­весия (8.6) преобразуется:

^{P^ + V-°e--gЈ = 0. (8.74)}

Используя условие пластичности, которое для вытяжки имеет вид о_р — о_в — o_s, можно исключить в уравнении (8.74) напряже­ние о_в:

P-^ + Ml + nctga) —a_plictga = 0, (⁸-⁷⁵) где а — угол конусности матрицы (угол между образующей и осью симметрии).

Разделяя переменные и интегрируя, получаем

ln[o_pp ctga- о_ь(1 + jictga)] = 1пр^^а -\-C_v

(8.76)

Произвольную постоянную интегрирования находим из усло­вия, что при р = Rx (на границе первого и второго участков очага деформации) величина напряжения о_р должна быть равна напряжению о_р, определяемому по формуле (8.73) при подста­новке в нее значения р = i?_t в сумме с приращением напряжения Лор, определяемым по формуле (8.52) (необходимость учета ве­личины АОр определяется тем, что при переходе элементов заго­товки из участка / очага деформации в участок // имеет место спрямление, при котором срединная поверхность получает уве­личение радиуса кривизны в меридиональном сечении от значе­ния до бесконечности).

Определяя произвольную постоянную интегрирования и под­ставляя значение С_х в (8.76), после преобразований получим

_{)['-Ш"""] +}

(8.77)

Формула (8.77) позволяет установить распределение напря­жений Ор в коническом участке очага деформации [в участке от R_t до R₂ (рис. 8.15)].

Распределение напряжений о_р в третьем участке очага дефор­мации (на скругленной кромке матрицы) можно найти на основе интегрирования уравнения равновесия (8.6), в котором R_p = = const, R_e = var, a = var, с использованием условия пла­стичности. Такое решение, в частности, дано в работе [99]. Однако без большой погрешности влияние изгиба и трения на кромке матрицы можно учесть аналогично тому, как это было сделано при анализе процесса деформирования заготовки в первом пере­ходе вытяжки. На скругленной кромке матрицы происходит изгиб и спрямление каждого элемента, проходящего через кромку матрицы, с изменением радиуса кривизны от оо до R_p — г_ы +

+ -|- и обратно.

Влияние изгиба и спрямления на величину максимального напряжения, возникающего на границе очага деформации со стен­ками образующегося стакана, можно учесть путем увеличения напряжений о_рв этой точке, определенного без учета изгиба, на

2/m + s "

Влияние трения на кромке матрицы приближенно учитываем множителем « (1 + 1 ца). С учетом сказанного формулу для определения cr_{p тах}, действующего при р = R_a, получим в виде

м-

_{-.!(> + +)}

(1 + м«)

(8.78)

Для приближенных расчетов формула (8.78) может быть зна-

чительно упрощена следующим образом. Так как

#3

1, то

в формуле (8.78) можно принять R_t — R₃. Эта замена увеличи­вает первое слагаемое в фигурных скобках и уменьшает второе.

Кроме того, так как

2Я₀

< 1, то без большой погрешности

{ R» \ ^tga V Ri I

в оценке величины а_ршах можно принять, что

м-

2Rp \ Rt ) '~ 2R_P • При таких допущениях формула (8.78) получает вид

•.--..{('+ -^)['-(-£Г"] +

+ -

2R_P

2r_M + в

(1 + да).

(8.79)

В формулы (8.78) и (8.79) входит радиус R_p участка свободного изгиба (см. участок / очага деформации), который не определя­ется однозначно размерными характеристиками инструмента. Так как величина а_р в участке / сравнительно мала, то радиус свободного изгиба может быть определен по формуле (8.39). Подставив это значение R_p в формулу (8.79), получаем

+

+ /w^{sina +} ^dT}^{(1 +} ^^a)-

(8.80)

Учитывая некоторые неудобства, связанные с возведением в дробную степень, формулу (8.80) можно упростить заменой степенной и логарифмической функции первыми членами раз­ложения в ряд по соотношению

V Ra I ' tg a R₃ tg a \ R₃ )

Произведя указанную замену в формуле (8.80), получим

Другие варианты упрощения формулы (8.78) даны в работах [17, 99]. Формулу (8.80) можно также получить, если принять, что конический участок распространяется на весь очаг деформа­ции, а влияние изгиба, спрямления и трения на кромке матрицы учесть аналогично тому, как это сделано при анализе первого перехода вытяжки.

Формулы (8.78), (8.80) и (8.81) позволяют определять вели­чину наибольшего растягивающего напряжения о_ртах, действу­ющего на границе очага деформации с учетом влияния сил трения,

изгиба и размеров рабочего инструмента (а; -у-)> ^н0 ^^ез У^чета влияния упрочнения.

Решение с учетом влияния упрочнения на величину о_ршах можно получить аналогично приведенному ранее решению для первого перехода вытяжки. Приближенно влияние упрочнения может быть учтено заменой напряжения текучести o_s в форму­лах (8.78) — (8.81) средним значением напряжения текучести для очага деформации.

Принимая линейную зависимость о_л = f(i|}) и учитывая, что

при вытяжке тангенциальная деформация е_е = ^^{3 р} явля-

ется максимальной, в основном определяющей увеличение напря­жения текучести вследствие упрочнения, можно установить, пользуясь формулой (1.13), значение напряжения текучести по границам очага деформации. Если заготовка до вытяжки была отожжена и напряжение текучести было одинаково по всему объему, то на границе очага деформации с недеформируемой частью исходной заготовки (при р = R₃) напряжение текучести равно a_{s mln} = о_т0, а на границе очага деформации со стенками вытягиваемого стакана (при р = Я_и) напряжение текучести равно

С! — гг 4- П ^³ ~ ^^и "ьгаах — ^ит0 Т "

Среднее значение напряжения текучести для очага деформа­ции, равное полусумме a_{s mln} и o_smax, определится по формуле

. „ I n Ra Ra ¹

°s ср — ^ит0 ~Г ¹¹ 2^ "

Подставляя это значение o_scp вместо a_s в формулы (8.78) — (8.81), можно получить расчетные формулы, приближенно учи­тывающие влияние упрочнения на о_ртах, действующее в опас-

ном сечении заготовки на после­дующих переходах вытяжки в конической матрице.

Из формул (8.78) — (8.81) видно, что а_ргаах увеличивается при прочих равных условиях с увеличением коэффициента тре­ния, с уменьшением относи­тельного радиуса скругления

рабочей кромки матрицы — и

^артах

0,7

0,6

0,5

с увеличением отношения .

OA

10 15 20 25 30 35 d°

0 5 Рис. 8.16

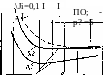
Особый интерес представляет характер влияния угла конус­ности матрицы а на величину напряжения о_ргаах. На рис. 8.16 приведены графики зависимости

^{0р ша}* ■ = f (ос) для последующих переходов вытяжки, получен-ные расчетом по формуле (8.78) при р = 0,1 и 0,2; — = 0,01 и

A3

0,1; коэффициент вытяжки k_B — 1,25 и 1,4 и = 2 и 5.

По графикам можно установить, что существуют оптимальные значения угла конусности матрицы ос, при которых при прочих равных условиях напряжение о_ри]ах имеет минимальную величину. Значения оптимальных углов увеличивают с увеличением коэф­фициента трения, габаритных размеров вытягиваемых стаканов

^с уменьшением отношения -^-j и коэффициента вытяжки k_B = р

— ——. При значениях \х > 0,2 увеличение угла конусности мат-рицы сверх оптимальных значений дает незначительное увели­чение напряжения о_ртах. Также незначительно увеличивается о_Ршах ^ПР^И увеличении а сверх оптимальных значений в случае вытяжки стаканов, когда < 0,01.

A3

р max

Указанный характер зависимости напряжения о₍

от ос-

новных факторов удовлетворительно согласуется с характером зависимостей, полученных экспериментально.

da,

1 + рос

1 и

Приближенное значение оптимальных углов конусности ма­триц а_опт можно найти аналитически, если в формуле (8.81) принять

р ™^ах- = 0. В этом случае

da₀

da

2R,

eos а

= 0.

Из этого равенства следует, что

sin² а_опт cos а_0П1 = д. ( 1 - -f .

(8.82)

Значение ос_опт по формуле (8.82) можно получить методом последовательных приближений.

Чтобы получить ос_0пт в явном виде, можно в формуле (8.82) принять cos а <=> I, и тогда

(8.83)

Нетрудно заметить, что формула (8.83) достаточно правильно отражает влияние основных факторов на величину оптималь­ного угла конусности матрицы, хотя и является весьма прибли­женной.

Проведенный анализ был выполнен в предположении, что изменение толщины заготовки в очаге деформации пренебре­жимо мало. В действительности толщина стенки уменьшается к донышку от края. Это приводит к тому, что в процессе вытяжки в очаг деформации поступают участки заготовки, имеющие все большую толщину, при этом к концу вытяжки о_ршах увеличи­вается. Это же обстоятельство является причиной того, что даже отожженные заготовки при вытяжке с предельными коэффици­ентами разрушаются в конце вытяжки.

Следовательно, при аналитическом выводе предельного коэф­фициента вытяжки необходимо дополнительно учесть перемен­ность толщины стенки заготовки вдоль образующей.

При вытяжке без промежуточного отжига необходимо также учесть переменность напряжения текучести вдоль образующей заготовки, вызванную различием тангенциальных деформаций, полученных элементами заготовки при предыдущих переходах вытяжки.