7.7. Скручивание

Скручиванием называется кузнечная операция, посредством которой одну часть заготовки поворачивают по отношению к дру­гой на определенный угол вокруг общей оси.

От ранее рассмотренных кузнечных операций скручивание отличается тем, что очаг деформации при этой операции не нахо­дится под непосредственным воздействием давящего инструмента,

а пластическое состояние по мере уве­личения угла закручивания постепенно распространяется от периферии заго­товки к ее оси, пока все сечение не будет охвачено пластической деформа­цией.

На рис. 7.55, а представлено изве­стное распределение касательных на­пряжений при кручении в поперечном сечении круглого стержня при упру­гой деформации. Напряжение макси­мально на периферии и по линейному закону падает, обращаясь в нуль в центре сечения. При увеличении угла закручивания касательное напряжение на поверхности достигнет предельного значения k, при котором начнется пластическая деформация. В случае отсутствия упрочнения и дальнейшего увеличения угла закручивания напряжение k охватит и более глубокие слои заготовки. Часть ее (периферийная) будет нахо­диться в пластическом состоянии, а часть (центральная) — в упругом (рис. 7.55, б). Наконец, при дальнейшем увеличении угла закручивания пластическая деформация охватит все сече­ние (рис. 7.55, в).

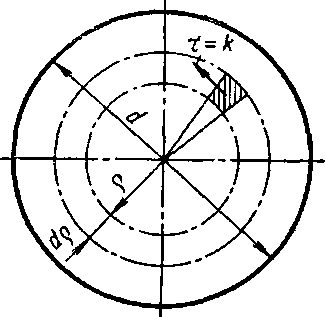
Необходимый для этого крутящий момент М легко найти, при­равняв его моменту внутренних сил (рио. 7.56):

0,5d 0,5d

М= | &ф.р.2яр = 2nk | p²dp,

о о

откуда

_M=«*._k-lg-ol (7.89)

Из формулы видно, что модуль сопротивления при пластиче­ском кручении больше, чем при упругом.

Глава 8

ОПЕРАЦИИ ЛИСТОВОЙ ШТАМПОВКИ

8.1. Дополнительные данные по методике анализа

Операции листовой штамповки можно разделить на две группы — разделительные и формоизменяющие.

Разделительные операции характеризуются от­делением одной части заготовки от другой путем разрушения материала по заданной границе (вырубка, пробивка, отрезка, зачистка и т. п.).

Формоизменяющие операции (гибка, вытяжка, обжим, отбортовка и т. п.) характеризуются тем, что заготовка получает пластические деформации и деформирование протекает без разрушения или потери устойчивости.

При формоизменяющих операциях пластической деформации обычно подвергается только часть заготовки — очаг деформации. Очаг деформации может быть заключен между частями заготовки, деформирующимися упруго, или же между свободным контуром заготовки и частью ее, деформирующейся упруго. Толщина заготовки в очаге деформации в формоизменяющих операциях обычно значительно меньше двух других ее размеров. При рас­смотрении формоизменяющих операций целесообразно ввести понятие срединной поверхности, делящей толщину заготовки пополам.

На рис. 8.1 схематично показаны характер формоизменения заготовки при выполнении основных формоизменяющих операций листовой штамповки, расположение очага деформации в заготовке и действующие внешние силы.

При гибке происходит изменение кривизны срединной поверхности заготовки, причем линейные деформации на средин­ной поверхности близки к нулю.

При вытяжке производится протягивание заготовки через отверстие матрицы, при котором плоская заготовка превра­щается в полое изделие, а пространственная заготовка (в после­дующих переходах вытяжки) получает уменьшение поперечных размеров.

При обжиме поперечные размеры краевой части полой тонкостенной заготовки уменьшаются путем заталкивания заго­товки в отверстие матрицы.

При раздаче внедрение пуансона в полую тонкостенную заготовку приводит к увеличению поперечных размеров заго­товки в очаге деформации.

При отбортовке производится вдавливание участка заготовки, граничащего с предварительно пробитым отверстием, в матрицу, при котором размеры отверстия увеличиваются с об­разованием борта.

Заготовка в очаге деформации обычно имеет контакт с по­верхностью одного рабочего инструмента, и лишь при деформиро­вании с принудительным утонением в очаге деформации имеются две контактные поверхности. Как правило, при деформировании поверхность заготовки в зоне очага деформации перемещается относительно поверхности инструмента.

На контактную поверхность заготовки со стороны инструмента действуют нормальные а_н и касательные т_к напряжения. Послед­ние возникают вследствие контактного трения.

Так как радиусы кривизны срединной поверхности в очаге деформации обычно значительно больше толщины заготовки, то нормальные напряжения на контактных поверхностях при де­формировании без принудительного утонения значительно меньше напряжения текучести.

При одной контактной поверхности напряжения, перпенди­кулярные к срединной поверхности, убывают по толщине заготовки от максимального значения, равного а_н, на контактной поверх­ности до нуля на противоположной, свободной поверхности.

Относительно малая величина напряжений, действующих нор­мально контактной поверхности, позволяет считать, что схема напряженного состояния близка к плоской, а касательные напря­жения на контактной поверхности согласно выражению (5.44) можно определять по соотношению

где ц, — коэффициент трения.

аза

В процессе перемещения элементов заготовки в очаге дефор­мации относительно поверхностей рабочего инструмента кри­визна их срединной поверхности может изменяться.

Изменение кривизны создается действием моментов и перере­зывающих сил и сопровождается неравномерным по толщине распределением деформаций и напряжений.

Воздействие моментов на деформирующийся элемент заготовки приводит к изменению величин продольных сил, а следовательно, и нормальных напряжений по сравнению со значениями, необ­ходимыми для пластической деформации элемента без изменения его кривизны.

При осесимметричной деформации тонкостенной заготовки в операциях листовой штамповки радиусы кривизны в широтных сечениях обычно больше, а величина изменения кривизны в про­цессе деформирования меньше, чем для меридиональных сечений заготовки. В этих случаях величины изгибающих моментов, действующих в широтных сечениях, меньше моментов, действую­щих в меридиональных сечениях.

Если же учесть, что на величине меридиональных напряжений действие широтных моментов скажется через проекцию широтных напряжений на касательную к образующей заготовки, можно полагать, что незначительное изменение широтных напряжений, вызванное действием широтных моментов, скажется на величине и распределении меридиональных напряжений в весьма малой степени.

Основываясь на сказанном, допустимо принять, что при отыска­нии распределения меридиональных напряжений в условиях осе­вой симметрии деформирования влиянием изменения кривизны в широтных сечениях можно пренебречь.

В большинстве случаев очаг деформации при осесимметричном деформировании можно разделить на участки, в каждом из кото­рых кривизна срединной поверхности в меридиональных сече­ниях постоянна.

Перемещение элементов заготовки относительно рабочих по­верхностей инструмента в таких участках очага деформации не сопровождается изменением кривизны срединной поверхности в меридиональных сечениях. Однако переход элементов заготовки из одного участка постоянной кривизны в другой (например, из плоской части фланца на скругленную кромку матрицы при вытяжке) вызывает изменение кривизны срединной поверхности в меридиональном сечении. Поэтому в первом приближении, решая задачу по отысканию распределения напряжений в очаге деформации, можно считать для каждого участка постоянной кривизны в меридиональном сечении справедливыми уравнения равновесия, полученные по безмоментной теории. Влияние же изгибающих моментов, действующих в меридиональном направ­лении, можно учесть граничными условиями между участками постоянной кривизны.

о

В общем случае при анализе операций листовой штамповки можно пользоваться уравнениями равновесия, пластичности, связи, неразрывности деформации и условиями на контуре, при­веденными в гл. 3—5.

Однако для формоизменяющих операций с осевой симметрией деформирования при наличии одной контактной поверхности можно получить приближенное уравнение равновесия элемента (рис. 8.2), выделенного в участке очага деформации, имеющего постоянную кривизну в меридиональном сечении. Элемент выделен двумя плоскостями, проходящими через ось симметрии заготовки ООх (меридиональные сечения), составляющими между собой угол dy, и двумя круговыми коническими поверхностями, образу­ющие каждой из которых перпендикулярны срединной поверх­ности заготовки (широтные сечения) и составляют между собой угол da,, а вершины этих конусов лежат на оси симметрии. При R_p = const положение рассматриваемого элемента можно задать его расстоянием р от оси симметрии и координатами центра кри­визны, причем каждому значению радиуса р соответствует опре­деленное значение угла а между касательной к образующей по­верхности в точке с координатой р и осью симметрии.

Изменение радиуса р на величину dp вызывает изменение угла а на величину da. Так как радиусы ^_р перпендикулярны касательной к образующей, то изменение угла da представляет собой угол между радиусами R_p, проведенными из точек р и р + dp. Примем, что толщина заготовки постоянна и значительно меньше радиусов кривизны в меридиональном R_p и широтном R_e сечениях. С учетом сказанного ранее считаем, что меридиональные напряжения а_р и широтные напряжения а₉ равномерно распре­делены по толщине заготовки и являются главными нормальными напряжениями.

Примем, что все нормальные напряжения (рис. 8.2) положи­тельны, а касательные напряжения ра_н совпадают по направлению с проекцией напряжений о₉ на касательную к образующей. Это допущение основано на том, что обычно в формоизменяющих операциях листовой штамповки о осевой симметрией деформиро­вания интенсивность увеличения напряжений о_р при изменении радиуса р возрастает за счет действия еил трения по сравнению б идеальным (без трения) процессом, при котором увеличение о₀ обусловлено только действием проекций напряжений о₉ на ка­сательную.

При составлении уравнений равновесия рассматриваемого элемента все элементарные силы (в том числе и силу трения) будем относить к срединной поверхности.

Уравнения равновесия рассматриваемого элемента (пренебре­гая бесконечно малыми высших порядков) следующие:

а) при проецировании на нормаль к поверхности (рис. 8.2)

а_н/з - 2о_р/_х -2cr_e/₂ -f - = 0; (8.1)

б) при проецировании сил на касательную к поверхности заготовки в меридиональном сечении

Vi + d (o_ph) - o_ph- 2o₉/₂ - |W, = 0. (8.2)

Соотношение между углами da, o"6 и dy можно найти из усло­вий, что длина элемента / в широтном сечении

/ = pdy = —^— аЪ = dQ;

^{i 1} cos а ¹ sin а '

отсюда следует

_dy== _^_ ₌ _Д_. (8.3)

' cos a sin а ^v '

Величины площадей f_u f₂ и f₃ определяются следующими очевидными соотношениями:

fi = ^s^e^{= S}Pdy; h = sR_pda — s­

dp

sin a

где s — толщина заготовки.

Дифференцируя первое уравнение, находим

df 1 = s dp dy.

Подставим полученные соотношения в уравнение равновесия (8.1):

o_aR_pR_Q da о"6 — a_psR_e d$ da — o_esR_p da d$ = 0,

После сокращения и несложных преобразований получим из-EiciHoe из безмоментной теории оболочек уравнение Лапласа

_^-т§—S-⁰_{- <}^s_-⁴_>

Подставим значения площадей f_lt /₂ и /₃ в уравнение (8.2) и выразим углы d6 и cf0 через dy по соотношению (8.3), учитывая, что & (Op/i) = а_р dfi + fx da_p:

a_ps dp dy + sp efa_p — a_es sin a dy —

■—uo_Hp dy ^rfp = 0. ^{r Hr} ' sin a

Р

Произведем сокращения и поделим почленно на s cfp: Подставим значение о_а из (8.4) в (8.5):

_%+"'-°-—^<8_-⁶⁾

Уравнение (8.6) является общим уравнением равновесия эле­мента заготовки постоянной толщины выделенного в простран­ственном участке очага деформации при осесимметричном дефор­мировании заготовки с наличием трения на контактной поверх­ности. Аналогичные уравнения равновесия были получены для частных случаев в работах 11, 113, 120 и др.].

Если рассматриваемая осесимметричная оболочка имеет пере­менную толщину вдоль образующей s = / (р) = Ф (ос), то анало­гичным путем можно найти общее уравнение равновесия для s = var, несколько отличающееся от уравнений (8.6). В этом слу­чае общее уравнение равновесия имеет вид

p-Ј+'.(¹+-S&)-*-Tg7(-Ј+-S-)-<»- м

Для отыскания распределения напряжений в участке очага деформации постоянной кривизны в меридиональном сечении необходимо применительно к заданной форме и размерам очага деформации установить связь между р, ос, R_p и R_e с тем, чтобы в уравнении (8.6) была одна переменная, характеризующая коор­динаты элемента, а также выразить одно из неизвестных напря­жений (а_е) через другое (а_р), используя условие пластичности.

Так как при относительно малой толщине заготовки (^~^~ <

< 0,2) и при R_p = const схему напряженного состояния прибли­женно можно считать плоской, а напряжения а_р и с_е — главными, то и условие пластичности должно быть принято соответствующим плоскому напряженному состоянию.

В зависимости от условий нагружения заготовки в различных операциях листовой штамповки схема напряженного состояния 340

и знаки напряжений ст_р и а_е в очаге деформации могут быть различными. В операциях вытяжки и отбортовки напряжения о_р — растягивающие, а в операциях обжима и раздачи — сжима­ющие. Напряжения ст_е являются сжимающими в операциях вытяжки и обжима, а в операциях раздачи и отбортовки — растягивающими. Таким образом, в операциях вытяжки и раздачи схема напряженного состояния разноименная (край­ние главные напряжения ст_р и ст₉), а в операциях обжима и отбортовки — одноименная (крайние напряжения ст_е и о„^ О, где ст_п — напряжение, перпендикулярное к срединной поверх­ности).

На рис. 8.3 представлен контур пластичности для плоского напряженного состояния по условию постоянства максимальных касательных напряжений и по условию постоянства интенсив­ности напряжений, а в каждом квадранте даны схемы операций, деформирование которых осуществляется при знаках напряжений, соответствующих определенным квадрантам.

Из схемы следует, что отрезки контура пластичности, заклю­ченные в каком-либо квадранте, характеризуют возможные со­отношения между напряжениями о_р и о_э в определенной операции листовой штамповки.

Пользуясь приближенным уравнением равновесия (8.6) и ус­ловием пластичности с учетом схемы напряженного состояния в данной операции, можно выяснить распределение напряжений в участке очага деформации с постоянной кривизной в меридио­нальном сечении. При резких изменениях кривизны в меридио­нальных сечениях должно быть учтено влияние изгибающих мо­ментов, что будет сделано после изучения операции гибки (пласти­ческого изгиба).