Вычислив по формуле (6.266) значения о\ для узловых то-

11 М. В. Сторожен 321

- Легко усмотреть, что построение поля, изображенного на рис. 6.21, можно продолжать, проводя из точки А радиусы-лучи (0,5), (0,6) и т. д., пока центральный угол кругового сектора ста­нет равным 135° и последний луч совпадет со стенкой штампа. При принятой на чертеже рис. 6.22 величине угла у = я/12 можно провести еще пять радиусов, и тогда, по выполнении построения, последней узловой точкой, расположенной на оси х, будет, точка (9,9).

(0,0) (1,1)	(2,2)	(3,3)	(4,4)
1 1,61	2,44	3,64	5,41
1 1,52	2,05	2,57	3,09
(5,5) (6,6)	(7,7)	(8,8)	(9,9)
8,12 12,24	18,85	29,2	45,67
3,62 4,14	4,67	5,19	5,71
напряжений	0г точек,	расположенных на

чек (5,5)—(9,9) и определив по таблицам [106] их абсциссы, по­лучим, учтя табл. 6.1, корреспондирующие значения нормальных напряжений а_г и координаты узловых точек, расположенных на оси х:

Точка х

0,5h₃

— Ог

2K Точка х

Q,5h₃

2k

оси х (оси симметрии поля), представлена на рис. 7.49. Изобра­женную кривую с достаточной точностью можно аппроксимиро­вать уравнением ¹

* = -a;(l + l,251n-jy. (7.74)

0,5h_:

рых а < 45,67ft.

Как видно, рассматриваемое поле справедливо для значений ^х < 45,67, т. е. для штампов, относительная ширина кото-

(т. е. ₀°'₅⁵^ < 45,67^ . В практике штамповки,

как сказано ранее, отношение а/п₃ доходит до 60—65.

Таким образом, поле линий скольжения, образованное двумя дугами равного радиуса, строго говоря, не удовлетворяет полному диапазону значений а/п₃, возможных при штамповке.

Дальнейшее расширение построения поля в сторону увеличе­ния значений a/ft₃ вполне возможно, но характер построения но­вых областей самого по­ля несколько изменится, в частности, очаг дефор­мации распространится вдоль стенки штампа ². Тем не менее уравнение (7.74) дает вполне удовлетвори­тельную точность и для значений х/0,5п₃ в интер­вале 46—65.

Уравнение (7.74) поз­воляет определить удель-

го

О

Рис.

322

¹ Уравнение этого типа предложил Е. М. Макушок [46]. Уравнение (7.74) отличается только постоянными.

2 Подробнее см. В работе

[46].

ное усилие р'_п деформирования металла в штампе при отсут­ствии подпора со стороны заусенца, деформируемого в мостике канавки, так как при вычислении а_г подпор не учитывался, а принималось о₀,₀ —— k.

Иа основании уравнения (7.74) и рис. 7.49 можно написать

Рп

После интегрирования, подстановки пределов

0,5h₃

= 1 и

0,5h₃

= — ПОЛуЧИМ

pi = a;[l,25(ln^-+-^)-0,26].

При размерах высоты заусенца, обычно применяемых на прак­тике ^-^->15), отношение hja практического значения не

имеет и им можно пренебречь (например, при = 15 ошибка

п.₃

меньше 3%). Тогда расчетная формула принимает вид

р'и = at (1,25 In -|- - 0,25) . (7.75)

Влияние подпора со стороны металла, деформируемого в мо­стике заусенца, можно учесть следующим образом. При отсут­ствии подпора напряжение а_г на участке графика (рис. 7.49)

от ~ = 0 до = 1 определяется величиной о*. В то же время

"3 "з

максимальное напряжение о_г в точке 0 согласно формуле (7.70) должно быть равно o_s* -\-а*-^~, т. е. на величину о* —

"3 "3

больше. Следовательно, на эту величину увеличатся значения на­пряжений и по всему диапазону значений координаты х, а также и удельное усилие р.

Поэтому, прибавляя к правой части уравнения (7.75) а*

д₃

получим окончательную формулу удельного усилия деформиро­вания металла поковки в полости штампа для случая плоской деформации (стержневые поковки)

^{Ра = а* (п?г~0,25 + 1,25 lni)- <7-76)}

Для поковок, осесимметричных, круглых в плане или при­ближающихся к ним, достаточно обоснованно предположение, что распределение напряжений а_г по оси р в этом случае будет та­ким же, как их распределение по оси х при плоской деформации, но вместо o_s* в уравнении (7.74) следует писать o_s. Кроме того, для получения возможности интегрирования по площади круга ось следует совместить с осью симметрии. Тогда уравнение (7.74) видоизменится следующим образом:

-аф + 1,25 1п(А__!_)].

Удельное усилие без учета подпора со стороны металла, де­формируемого в мостике заусенца, выразится следующим образом:

л

к-¹

Рп = O_s

^{1 +} _{Л^Т f} ^1,251n_(i-Tk)^x

После интегрирования и подстановки пределов получим р'_п = a_s [l,25 (in ± + 2 А - 0,5 - 0,875 h №

Разность 2 -j 0,5-Jr ^ПР^И принятых размерах канавок для

заусенца, особенно для круглых в плане поковок, у которых dlh₃ обычно больше, чем a/h₃ для поковок удлиненной формы, практи­ческого значения не имеет и ее можно отбросить. Например, при

~ = 20 ошибка меньше 2%. Тогда формула принимает вид

"3

Й = a, (l,25 In-£-- 0,875). (7.77)

Подпор учтем так же, как и при выводе формулы (7.76), но с использованием уравнения (7.72). В результате получим окон­чательную формулу удельного усилия р_п деформирования ме­талла поковки в полости штампа для случая осесимметрич-ной деформации (круглые в плане поковки)

Рп = °, [-^f- 0,375 + 1,25 In {-]. (7.78)

Определим удельное усилие деформирования металла в штам­пе рп также и методом верхней оценки, следуя А. И. Око­нечному (86]. Эта задача решается аналогично задаче, решение которой показано на примере внедрения пуансона в полупростран­ство (см. стр. 220).

Примем дополнительно следующие обозначения:

h₃ = 0,5/г₃; 1г₀ = 0,5/г₀; а = 0,5а. (а)

Рис. 7.50
	/
0 h0-h3

В силу симметрии рассмотрим только один правый верхний квадрант.

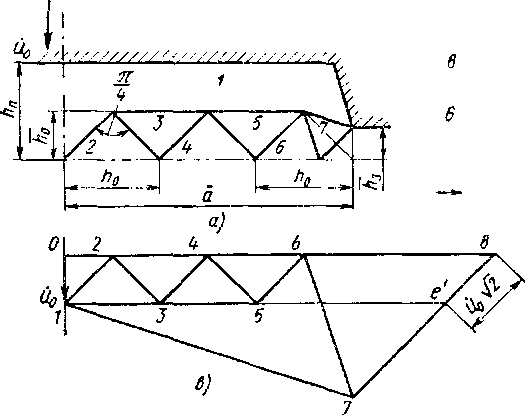
Разделим половину ширины поковки а на п равных частей длиной /г₀ = 21г₀ и построим разрывное поле в виде треугольных блоков, как показано на рис. 7.50, а. Для большей ясности по­строения блоков 6 и 7 приведен рис. 7.50, б. На основании при­нятого поля строим годограф скоростей и( рис. 7.50, в).

Удельное усилие определяется в соответствии с выраже­нием (6.32)

(б)

, ^тс Zj ^unln , °"s Zj ^unln

рп = =: ИЛИ р_п = - ^

quo 2o«o

Напряжение сдвига т_с везде одинаково и равно k = 0,5а*. Напишем составляющие общей суммы 2j ^uJm пользуясь рис. 7.50, айв:

S1 ⁼ "12/12 ~\~ "23/23 ~\~ "34^34 ~т~ "45^45 ЧЬ "бе^бе — 2/l₀u₀'5. В этой сумме все слагаемые равны между собой, так как /„ = = Ъ₀ У~2 и u_n = u₀ ]/2.

В общем случае, учитывая, что а — 2nh₀,

Si = 2h₀ii₀(2n — 1). Далее

S 2 = "13^13 4~ "15^15-

Здесь

l_n = 2h,

о> "13 — 2u₀, и±

*1б — ^"о>

и далее, если бы число делений было больше, каждое последую­щее и увеличивалось бы в арифметической прогрессии на вели-

325

чину 2и₀, а число блоков на единицу меньше числа делений п. Поэтому, пользуясь правилом о сумме арифметической прогрессии, для произвольного п в общем виде можно написать

= 2h₀u₀-n(n — 1).

Наконец, последняя составляющая

Пользуясь рис. 7.50, а и б, легко установить, что /67 = In = Vht + (Л„ - h₃f\ l₁₈ = \V2.

Скорости щ₇ и щ₈ определим из подобия треугольников 6 7 8 на годографе (рис. 7.50, в) и bed на рис. 7.50, б, а скорость u_i7 — из подобия треугольников 1 Те' (рис. 7.50, в) на годографе и ted на рис. 7.50 б:

• be • • ей

Скорость и_№ представляет собой разность скоростей и_оа—и₀д. Величина скорости и_ов очевидна: ы₀₆ = 2и₀ (п — 0,5).

Скорость и_т является скоростью металла на входе в канавку для заусенца, и по условию сплошности обязательно равенство

которое удовлетворяется автоматически при отсутствии ошибки в построении годографа, что легко проверить по чертежу. На осно­вании приведенного равенства и учитывая, что a = 2h₀n, получим

• _ г, ' n(h₀ — h₃)— 0,5h₃

"68 — ^^и0 г '

По рис. 7.50, б легко получить длину отрезков be = hi = Vl% + (Ло -Ту²; fcd = 2\-h₃; dc= h₀ V2 ', be = bc и ed = (ft₀ — А~з) 1^2.

я;)²

h₀-h₃ + 0,5-f h₀ — 0,5/t₃

+ ■

Осуществив подстановки полученных значений / и и в сумму 2]₃ и произведя необходимые преобразования, получим

]£з = 2/г₀«₀п

Л„ ft,

Собирая слагаемые 2лгз ^и произведя деление на 2аи₀ согласно выражению (б), после элементарных преобразований получим

Рп — C_s

0,5 + 4- +

2/ln/ls

ft₀ — 0,5/i₃

Последним членом в квадратных скобках можно пренебречь, поскольку его величина не превышает (0,2—0,3). Тогда

L 4ft„ 2h„h₃ J

(в)

Теперь находим значение параметра h^, определяющее мини­мальную величину р„, дифференцируя правую часть полученного уравнения по dh₀ и приравнивая производную нулю. В резуль­тате получим

0.5

Подставляя это значение п$ в формулу (в) и учитывая соот­ношения (а), окончательно получим

_р^{; =} ₀^{; I/2+4-од}

(7.79)

Данное выражение, как и выражение (7.75), полученное ме­тодом линий скольжения, не учитывает подпора со стороны за­усенца. Учесть его можно так же, как это сделано для выраже­ния (7.75) на стр. 323.

На рис. 7.51 показаны графики, вычисленные по форму­лам (7.75) — кривая 1 и (7.79) — кривая 2. Естественно, что зна­чения удельных усилий, полученных методом верхней оценки, больше найденных методом линий скольжения. Следует заметить, что при учете подпора со стороны заусенца и удельного усилия деформирования самого заусенца разница в результатах, полу­ченных обоими методами, значительно сглаживается.

6

Решение, весьма близкое к при­веденному (7.79), на основе разрыв­ного поля другого вида дали Е. С. Ро­манов и А. М. Меркулов [80]:

_{Р» = V-тг •}

7.6.4. Полное усилие штамповки

го

зо

Полное усилие доштамповки Р — — Р₃ + Р_п (стр. 316) определяется формулами:

а) для поковок удлиненного типа, имеющих в плане форму прямоугольника или приближающихся к ней [используются уравнения (7.71) и (7.76)],

P = o;{(l+»_s -±-) F₃+(²JgL_0,25 +

+ l,251n-Ј-)F_n}; (7.80)

б) для поковок, круглых в плане или приближающихся к ним [используются уравнения (7.73) и (7.78)],

^{P = a}_s^{{(l,5 + ,}_s ^{Ј)f.+ (JЈL-}

-0,375 + 1,25 In -~)F_n}- (7.81)

В формулах (7.80) и (7.81) F_n — площадь проекции поковки (или рассматриваемой части ее при расчленении сложной поковки на элементарные участки) в плоскости разъема; F₃ — площадь проекции мостика заусенца.

Формально было бы правильнее в формулах (7.80) и (7.81) не выносить o_s за общую скобку, так как средние значения напря­жения текучести металла в заусенце и в самой поковке будут не­сколько различны. Однако доля усилия, необходимого для де­формирования заусенца на мостике, относительно мала по сравне­нию с долей усилия, необходимого для деформирования металла в полости штампа. Поэтому возможная разница в значениях a_s мало повлияет на общую величину деформирующего усилия.

Вместе с тем резкое остывание заусенца происходит лишь после окончания деформирования, а в процессе деформирования в за­усенец непрерывно поступает горячий металл из полости штампа, а значительная скорость деформации заусенца способствует со­хранению температуры.

Формулы (7.80) и (7.81) получены комбинированным методом: напряжения в металле, деформируемом в мостике заусенца, вы­числены путем решения приближенных уравнений равновесия совместно с условием пластичности, а напряжения в металле, вы­тесняемом из полости штампа, определены методом линий сколь­жения.

Возможно также построить непрерывное поле линий скольже­ния, включая и объем металла, деформируемого в мостике за­усенца. Однако это повело бы к некоторому усложнению конеч­ных выводов, не давая каких-либо практических преимуществ.

Формулы (7.80) и (7.81), равно как и формулы (7.74)—(7.78),

действительны в диапазоне = 15 -t-65 и только в тех случаях, когда глубина полостей верхнего и нижнего штампов по выступам 328

>

<

Ля

А,

(/г_пв и h_m, рис. 7.52) больше половины высоты пласти­ческой зоны /г₀, т. е. при соблюдении неравенства

0.5/ь

Изучение поля линий скольжения, образованно­го дугами двух окружно­стей равного радиуса, по­казывает, что максималь­ная высота пластической зоны п₀, определяемой этим полем, и расстояние А по горизонтали между крайними точками С для обычно встречающихся в практике штамповки соотношений alh₃ (равных 15—65) определяются достаточно точно следующими соотношениями:

h₃

А

h₃

= (0,28 -s- 0,29) = (0,67 0,64)

а h₃ а

(7,82а) (7.826)

Формулы для определения усилия штамповки методом линий скольжения впервые получил Л. А. Шофман [17], пользуясь гра­фическим построением поля. Предложенные им формулы не­сколько сложнее. Они дают значения удельных усилий, близкие к получаемым по формулам (7.80) и (7.81).

Если глубина полостей штампа мала и пластическая зона входит в соприкосновение с дном верхней и нижней полостей штампа, то

при h_nB = h_na = -i- h_n (рис. 7.52) поле линий скольжения (р, =

= 0,5) примет вид, показанный на рис. 7.53, а [121]. Область

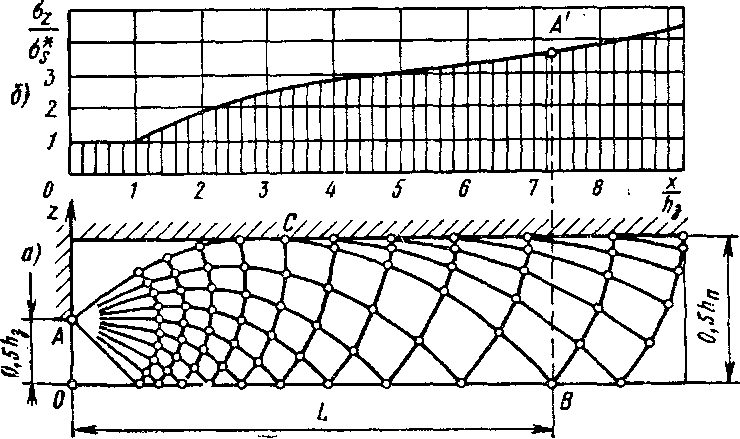
OA С В представляет собой участок поля, образованный дугами двух окружностей равного радиуса, и не отличается от рассмотрен­ного по рис. 6.21. Далее следует второй участок поля, соответ­ствующий случаю осадки полосы между шероховатыми плитами, как на рис. 6.19. Поэтому на основе уравнений (7.74) и (7.8) для второго участка можно написать

а_г = -а;(1 + 1,25Ш^+^). (7.83)

Длину L начального участка можно определить из (7.82а): = (3,58 -н 3,44) (7.84)

Большие значения коэффициента для меньших значений hjh₃ в пределах примерно 3—16. Эпюры напряжений о_г представлены на рис. 7.53, б.

Чем меньше относительная высота заусенца hjh₃ и чем больше относительная ширина поковки а/п₃, тем большую протяжен­ность и значение получает второй участок поля и тем больше удель­ное усилие штамповки. Предельной величины оно достигает при

^{4~ = 1, т. е. когда штамповка в открытом штампе по существу}

превращается в осадку весьма тонкой полосы. Поэтому предель­ное усилие штамповки ограничивается значениями, которые можно получить, применяя формулу осадки, принимая за высоту по­ковки высоту заусенца:

Я_пред= 1,15а, (1+0,25-5L+?L);

Я_пр;д = а₅(1+0,17-Ш1)

соответственно для случая плоской и осесимметричной дефор­мации.

Вместе с тем, пользуясь формулами (7.74), (7.82) и (7.83), можно получить общие выражения усилия штамповки как для плоской, так и для осесимметричной деформации. Для плоской деформации (пользуясь приведенным выше материалом) это будет достаточно просто, для осесимметричной — несколько сложнее.

Для поковок сложной формы, в частности таких, у которых выступы штампа пересекают плоскость разъема, также возможно, как показал Л. А. Шофман, в конкретных случаях графическое построение поля линий скольжения и определение по этому полю усилия штамповки [17, 121].

7.6.5. Элементы штамповки в закрытых штампах²

Усилие штамповки в открытых штампах определено выше для периода доштамповки, когда излишек металла вытекает в заусенец при уже полностью оформленной поковке. При штамповке в обыч-

ных закрытых штампах доштамповка отсут­ствует, и процесс закапчивается, как только заполнена полость ручья, причем в послед­нюю очередь углы. Отсюда следует, что не­обходимое усилие для осуществления нор­мального процесса при штамповке в закрытых штампах меньше, чем при штам­повке в открытых штампах.

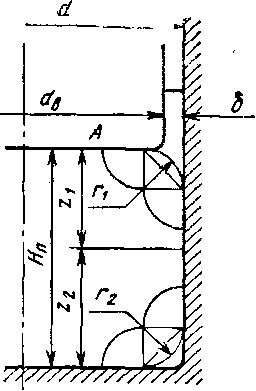
Большое влияние на величину усилия оказывают радиусы закругления г в углах (рис. 7.54) и несоответствие объемов дефор­мируемого металла и ручья (избыток метал­ла в заготовке). Как теоретически и экспе­риментально доказали Л. И. Живов и А. 3. Журавлев, с уменьшением величины р_ис 754 радиуса г значительно растет необходимое удельное усилие, обеспечивающее заполнение углов. Это усилие зависит также от сложности формы поковки, от характера за­полнения полости (осаживанием или вдавливанием), от количе­ства полостей с наличием входящих углов. Начало изучению этих вопросов положил А. В. Ребельский [76].

Силовые условия штамповки осаживанием в закрытых осе-симметричных штампах оптимальны, если после оформления за­кругления в углу наиболее труднодоступного участка действие внешней силы прекращается.

Для этого случая величина удельного усилия следующая:

Рп = (1 —х")² + ^Gs

1,5 In +

2r_x

Hi

+ 12

12-

^{_ 4,5 4-+ 1,91 -^- +}

6#_n

1,5

(7.85)

где г] — радиус закругления поковки у пуансона; d — диаметр поковки; Н_п — высота поковки; ipa_s = 2,070,, — контактное на­пряжение в точке А при максимальном трении.

В процессе заполнения угла в зоне пуансона обычно запол­няется и угол у дна матрицы. В результате сдвига деформируемого металла относительно стенок матрицы возникает трение, и удель­ное усилие на подвижном пуансоне увеличивается

р_п = ^(1—^l)+o_s

1,51п-^ ' 2r₂

+ 12-A.-12-JL

4,5

fin

Hi

+ 1.92-^ +

6Я_П

+

+ 4 (tf „ -'i -'*) - 1,5

(7.86)

где r₂ — естественный радиус закругления угла у дна матрицы.

331

Нормальные напряжения на стенках ручья при максимальном трении и заполнении углов опишутся следующими уравнениями: при построении от угла у пуансона

= 1,48 1п -|- + 2,07; (7.87а)

при построении от угла у дна матрицы

= 1,48 In -т^ + 2,07, (7.876)

здесь z — расстояние вдоль стенки от соответствующего угла до рассматриваемой точки.

На стенках существует раздел течения металла в углы. В точке раздела трение равно нулю, а нормальное напряжение макси­мально. Формулы (7.87) позволят построить эпюру нормальных напряжений на стенке закрытого ручья при заполнении углов и определить боковое усилие.

Усилие штамповки в закрытых штампах начинает резко воз­растать, если действие внешней силы продолжается после заполне­ния полости штампа, и металл начинает затекать в узкий зазор между пуансоном и матрицей, образуя быстро охлаждающийся торцовый заусенец.

С целью уменьшения трения в торцовой щели иногда на пуан­соне делают узкий поясок. В этом случае можно считать, что тре­ние в зазоре между пуансоном и матрицей близко к нулю. Тогда

удельное усилие при штамповке высоких поковок—^¹- > 0,2 равно

ч

Рп = iK + Osif [l,48 In-

.71(11-1) т

+5,06 i^i - 2,16 ^(Т)~'⁾² - 2,22] , (7.88а)

где т] = d/d_B; d — диаметр полости ручья; d_B — диаметр пуансона; б = (d — d_B)/2 — зазор; гр = 2,85.

Из формулы (7.88а) видно, что удельное усилие постоянно и зависит только от величины зазора.

Если область пластической деформации распространяется на

всю высоту поковки < 0,2^, то удельное усилие равно

р_п = + чЧ

1,50 In ^15Нп

1,71(11-1)

+ 5,06 ^_₂₎₁₆1^_1)1_ 4,5-^ +

(7.886)

В этом случае шестой член в скобках показывает рост усилия с уменьшением высоты поковки. 332

Если ручей имеет уклоны, то в процессе штамповки боковые поверхности в зазоре сближаются. Тогда кроме увеличения длины торцового заусенца происходит уменьшение его толщины. Обра­зующийся тонкий торцовый заусенец, преодолевающий трение в зазоре, и приводит к быстрому разрушению штампов.

При штамповке на гидравлическом прессе возможно устано­вить регулировочный предохранительный клапан на усилие, тре­буемое для штамповки данной поковки.

Кривошипный пресс в случае преувеличенного объема заго­товки будет работать «в распор», и возможна даже его поломка. Для обеспечения безопасной работы кривошипного пресса приме­няют два способа. Первый заключается в том, что в штампе преду­сматривают магазин (компенсатор) для принятия излишнего ма­териала в заготовке. Другой способ состоит в применении пресса такой жесткости (податливости), чтобы колебание высоты поковки находилось в пределах безопасно допустимых упругих деформа­ций пресса. Однако в этом случае требуется кривошипный пресс с повышенным номинальным усилием [231.

При штамповке в закрытых штампах на молоте трудно устано­вить момент заполнения полости и возможно нанесение лишних ударов, что сопровождается резким увеличением усилий и напря­жений в металле штампа в тем большей степени, чем больше масса падающих частей молота. Поэтому А. 3. Журавлев рекомендует ограничивать последнюю пределами

G = (3,5-5,0) F_n,

где G — масса падающих частей молота, кг; F_n — площадь про­екции поковки, см² [23].