10 М. В. Сторожев

289

0		г Pi
—i		-4- 4
мл			#

Рис. 7.32

Л₉, = P,

где Л ₂—работа равнодейст­вующей Р₂ активного дав­ления на верхнюю (по рис. 7.32) поверхность очага деформации; A_D — работа де­формации формы; Л_х—рабо­та сил контактного трения на конической контактной по­верхности; наконец, А_х — работа сопротивлений со сто­роны цилиндрического уча­стка 1.

Допустим,что за какой-то весьма малый промежуток времени равнодействующая Р₂, направленная по оси г, осуществит работу на пере­мещении и_г. Тогда работа Л ₂ выразится так:

(б)

Составляющие правой части уравнения (а) определим, исполь­зуя формулы (6.41) и (6.42). Работа деформации

_Ш

a_s2e₍- dV.

Так как в данном случае е_е = е_ф, а е_е + е_ф -f- е_р = 0, то ^ее — ^бф ⁼ —0,5е_р ^и интенсивность деформаций 8/ по выраже­нию (4.11) представится в виде е_г — =te_p.

В свою очередь, по формуле (4.4)

откуда

+ 2 = 0;

ap ' р

0.

это уравнение можно представить в виде д («рр»)

до

Интегрируя, получаем и_РР² = f (ф).

На верхней граничной поверхности очага деформации (р = Ь) при ф = 0 перемещение «_р = и_г. Следовательно, в точке р = Ь и ф

/ (Ф) = / (0)

и_гЬ^%.

Допустим, что и во всех точках верхней границы очага дефор­мации перемещение и_р не зависит от ср, оставаясь равным и_гЬ^г* . Тогда

9. 1 9.

и_рр = up

и, следовательно, и_р = ир²р~²;

dup

\^Bp\⁼⁼-^-^=s2u^P ^=ef (^в)

Для определения dV выделим элементарный объем, ограничен­ный сферическими поверхностями с радиусами соответственно р и р + dp и конической поверхностью матрицы (рис. 7.32).

Значение этого элементарного объема

dV = (площадь m_pf_pra_p) dp,

площадь nipfptip представляет собой площадь шарового сегмента,

т. е. п^_рп_р = 2nph,

но

h = р — р cos у = р (1 — cos у), следовательно,

dV = 2л (1 — cos у) р² dp. (г)

Таким образом, после подстановки (в) и (г) в уравнение (6.41) получим

*

dp

^A_D ^{= о^пир"1 (1 - cos у) j ^. (д)}

Работа трения, согласно уравнению (6.42), будет Ат = \ \ т_кы_кр dF,

F

где т_к — элементарная сила трения (напряжение, численно рав­ное касательному напряжению на контактной поверхности); и_кр — перемещение и_р на контактной поверхности:

"кр = «р = ^и^²Р~²,

и дифференциал площади (рис. 7.32)

* 291

dF = nD_p dp = 2яр sin у dp.

После подстановки получим ь

А_т = х_я2пи_гЬ² sin у | — • <е)

Напряжение т_к считаем постоянным, поэтому и выносим его за знак интеграла.

Наконец, для работы сопротивлений со стороны цилиндриче­ского участка 1 имеем

л ^nd2

К = Pi — щ.

Перемещение и_х равно перемещению и_р при р = а, т. е.

_ й² щ — u_{z а2} ;

Л = Pi —"г-^Т- (^Ж)

Теперь, подставляя уравнения (б), (д), (е) и (ж) в (а), получим

ъ

Р₂и_г = сг₅₂4пн_г6² (1 — cos 7) [ — +

j Р

а

b

о U2 ■ f ^d9 1 ⁶²

^{+ T}_K^.2_n^{^sin}₇^{J -y + Pi—-^г«}_г^,

откуда после интегрирования и деления [на и_г и учитывая, что

01 ь , б²

21п— = 1п-_т, имеем

б² nd² fc²

Р₂ = [т_кл6² sin 7 + o_s2 • 2л6² (1 — cos у)] In -^г + Pi — -^г»

но (рис. 7.32)

D² D²

4 sin² v 4(1 — cos² 7)

и

fc^a Р^г _ F

а² ~ d² ~' f '

поэтому после деления на площадь приемника t = — ₄ (которую считаем равной площади пуансона) получим удельное усилие

_{р==(_1«—|-} ^2g_*² _{\ in 4- + Pi- (}⁷_-⁵⁴₎

^Г2 \ sin у ¹ 1 -4- cos у ) / ^{1 п v} '

Эту формулу ранее вывел И. Л. Перлин, использовав другой метод [661. 292

Для практического использования формулы (7.54) необходимо задаться тем или иным значением т_к.

Так как напряжение о_ф больше напряжения а_р (см. схему /, 7 на рис. 5.12 — максимальной деформации растяжения соответ­ствует минимальное по абсолютной величине напряжение), то его величина не может быть меньше о_ь3 даже на выходной кромке конического участка матрицы, не имеющей калибрующего пояска. Сказанное дает основание принять для подстановки в фор­мулу (7.54) некоторое среднее значение т_к в виде

^т« = Н-Лг- (7.55)

Подставляя (7.55) в (7.54), получим

Р₂ = o_Si (~^~ + ) ^1п ~г~ + Л- (7-56)

^^{z si} \ sin у ¹ 1 -j- cos у ) \

Из вывода формулы (7.56) [учитывая формулы (7.54) и (7.55)] следует, что в раскрытом виде член

^J_S2

(lHV)^lnf =А«р (⁷'^56а)

учитывает трение в матричной воронке. В свою очередь, член

^ 1₊²_C0ST ^1П Т ^{= Р2Д (7}'^56б)

определяет удельное усилие, необходимое непосредственно для деформации выдавливания, но с учетом дополнительных сдвигов. И. Л. Перлин считает, что зависимость удельного усилия р_2д от

угла у, определяемая коэффициентом ■ ² = —!—-, отра-

* ^ cos² -|-

жает существующие представления о течении процесса выдавли­вания через коническую матрицу и о росте дополнительных сдви­гов с увеличением угла у [66].

При штамповке выдавливанием центральный угол 2-у не должен превышать так называемого угла естественного тече­ния. При углах 2у больших, чем последний, образуются «мертвые углы» или жесткие зоны недеформируемого металла. Отсутствие же­стких зон обеспечивается при 2у < 110°, хотя в некоторых случаях они могут отсутствовать и при значениях 2^, достигающих 130°.

При прессовании же прутков, профилей, труб, когда остаток металла в приемнике (контейнере) удаляют в отход («пресс-оста­ток»), угол 2у можно делать больше угла естественного течения, так как возможный скол уйдет в отход.

Для малых углов 7 (при у < 30°), допуская отклонение меньше 6%, формулу (7.56) можно упростить, принимая sin у я» у и cos у я« 1:

p₂ = <j₆₂(l +^)1п-у- + _Л. (7.57)

Если в формуле (7.57) не учитывать трения по стенкам матрицы и в калибрующем пояске, то она примет вид Р

p₂ = o_s2ln —; (7.57а)

это будет идеальный случай, когда деформация протекает вполне равномерно.

7.4.4. Цилиндрический участок-приемник

Условия течения металла в приемнике отличаются большой сложностью.

Как показывают опыты на образцах с нанесенной координат­ной сеткой, если коэффициент контактного трения относительно невелик, а пластические свойства однородны по всему объему металла, то металл проталкивается пуансоном по приемнику и в нем практически не образуется очаг пластической деформации. Координатная сетка остается почти не искаженной (рис. 7.33, а).

При увеличении контактного трения, а также при некоторой неоднородности пластических свойств металла наблюдается ясно выраженная пластическая деформация, причем слои металла, рас­положенные в осевой части приемника, текут более интенсивно по сравнению со слоями, примыкающими к его стенкам, что ясно видно по искажению координатной сетки (рис. 7.33, б).

Наконец, при больших коэффициентах трения и значительной неоднородности пластических свойств металла в центральной и пе­риферийной зонах, например в результате охлаждения послед­них за счет отвода теплоты стенками приемника, наблюдается рез­кое развитие пластической деформации металла по всему объему приемника при значительной неравномерности ее. Металл в зо-

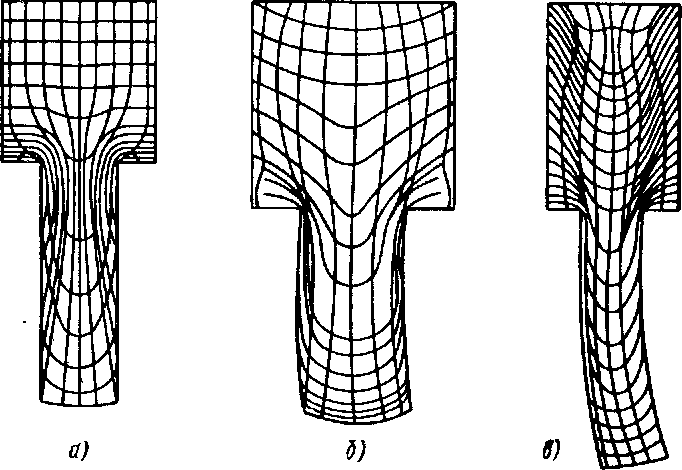
нах, примыкающих к поверхности приемника, иногда течет в на­правлении, обратном движению пуансона, а затем меняет направ­ление своего движения, питая центральную зону, где движение частиц металла совпадает с направлением движения пуансона. Искажения координатной сетки для такого случая представлены на рис. 7.33, в.

При очаге деформации данного вида деформированный металл, особенно цветной, отличается большой неоднородностью по вели­чине зерен и наличием значительных остаточных напряжений.

На практике штамповки выдавливанием и прессования на­блюдаются премущественно первый вид очага деформации в при­емнике, что достигается применением современных смазок.

Поскольку пластическая деформация в приемнике в таком слу­чае практически отсутствует, можно считать, что металл передви­гается как одно целое, находясь в состоянии всестороннего упру­гого сжатия.

Некоторые исследователи раньше предполагали, что давление металла на боковые стенки приемника превышает осевое, т. е. что о_р > o_z. Это положение, однако, не соответствует действи­тельности, что можно показать следующим образом.

Пусть к торцам некоторого цилиндра приложена равномерная нормальная нагрузка р, а по боковой поверхности равномерное давление р и соотношение между р и р таково, что происходит сжатие цилиндра, т. е.

е_г < 0, а е_р — е₀ > 0.

Из уравнений равновесия (3.39) явствует, что при такой на­грузке напряжения не зависят от координат:

о* = — р; о_р = а_е = — р'. Определим деформацию е_р = е₀:

Ер = [Ор — |А_р (О_г + Од)],

и так как а₀ = о_р, то

^ер = TfK¹ — М-_Р)°"р— \¹p°z\

(ц,_р •—коэффициент Пуассона).

Пусть деформация е_р равна нулю. Это будет аналогично поме­щению образца в жесткий (недеформируемый) приемник. Тогда получим

(1 — [ip)Op- }ут_г = 0, откуда

Так как ц_р < 0,5, то из последнего выражения ясно, что °р <2 ^аг> ^и лишь в предельном случае при ц_р = 0,5 и значитель­ном увеличении а_г о_р ZX °V При упругом приемнике всегда Ор < о_г.

Так, Л. В. Прозоров [75] указывает, что при благоприятных условиях трения давление на стенки приемника заметно меньше осевого и лишь при выдавливании без смазки приближается к осе­вому.

Что касается осевого давления р₃ на торец пуансона, то оно, естественно, больше давления р₂ вследствие трения металла о стенки приемника:

Рз = Рг + Ртр-

Усилие трения уменьшается по мере уменьшения длины L при движении пуансона (см. рис. 7.31) приблизительно по линей­ной зависимости, но [75] при хорошей смазке незначительно (при изменении вдвое длины L усилие трения изменяется на 3—5%).

Многочисленные эксперименты Л. В. Прозорова показывают, что элементарные силы контактного трения в приемнике 3 при нормальных условиях выдавливания не превышают 0,5o_s3. Ска­занное позволяет принять напряжение трения т_к постоянным и равным с некоторым преувеличением 0,5o_s3. Тогда усилие тре­ния (см. рис. 7.31)

Р_тр = 0,5o_s3nDL,

откуда делением на л£)²/4 получим

_ ²¹

Ртр °s3 >

и, следовательно, удельное усилие на пуансоне 2L

Рз = Рг + tf_s3 -7j- • (7.58)

7.4.5, Удельное усилие деформирования

при различных формах инструмента

Инструмент по рис 7.34, а. Эта форма инструмента является основной для штамповки выдавливанием поковок в виде цилиндрического стержня с утолщением на одном конце. В ка­честве расчетной используем формулу (7.58) с подстановкой зна­чения р₂ из формулы (7.56) и учетом формулы (7.53):

_{р = °«(-ёт + T+W)}^1п _{т +}^а_{- +} ^а_«*т- ⁽⁷_-⁵⁹⁾

Если заходной угол матрицы 2у больше угла естественного течения, то в формулу (7.59) следует подставлять последний (100—130°).

5) в)

Инструмент по рис 7.34, б. Эта форма отличается от предыдущей тем, что к цилиндрическому участку 3 (приемнику) примыкает участок 4 малой конусности. Такой инструмент может служить для получения поковок типа ступенчатых валиков с ко­ническим переходом между участками. Расчетную формулу по­лучим подстановкой в уравнения (7.58) значения р₂ из равен­ства (7.57) и рх из (7.53):

р = cx_s2 (1 + Јfj in I- _{+ Cs3} Щ. _{+ 0д} JBL, (7.60)

При отсутствии цилиндрического участка 1 (для получения поковки валика с коническим концом) достаточно положить в фор­муле (7.60) I = 0.

Инструмент по рис 7.34, в. Такую форму инстру­мента применяют для получения поковок с коническим переходом от утолщения к цилиндрическому стержню. Инструмент отли­чается от изображенного на рис. 7.34, а тем, что между участками большой конусности 2 и цилиндрическим / введен дополнительно участок малой конусности 4.

Для получения расчетной формулы необходимо использовать выражения (7.58), (7.56), (7.57) и (7.53):

_{р = а$}J(-^-₊_-²_\ln -L + (l + J^l\ In ₊ ^{H s}" L \ sin v ¹ 1 + cosv j / ¹ V У J f J

+ e_s3~ + o_sl*Vf; (7.61)

здесь 2y' — угол конусности промежуточного участка 4; f — пло­щадь, соответствующая промежуточному диаметру d! (рис. 7.34, в).

Для получения поковки в форме утолщения с коническим стержнем без цилиндрического конца участок 1 не нужен, и для определения р в формуле (7.61) следует принять / = 0.

В выведенных формулах указаны коэффициент трения р,] и фактор трения p_s2. Коэффициент р_х характеризует трение в ци­линдрическом выходном участке /. Здесь пластическая деформа­ция отсутствует, и, следовательно, р_х представляет собой обычный коэффициент трения при механическом скольжении. Наоборот, фактор трения p_s2 характеризует трение при пластической де­формации (горячей или холодной) в конических участках инстру­мента.

Обозначение напряжения текучести o_s также индексировано дополнительно цифрами 1, 2 и 3 в зависимости от участка, к кото­рому оно относится; о_с3 относится к исходному металлу при той средней температуре, которую он имеет в приемнике. Практически при горячем выдавливании в качестве o_sS можно взять предел проч­ности металла при температуре деформирования.

Наоборот, ст_ь1 относится к материалу деформированному. По­этому при назначении o_sl в случае выдавливания с упрочнением

следует его учесть исходя из средней степени деформации удлине-

P f р

ния —~- или по средней логарифмической деформации In — .

На втором участке, т. е. в зоне деформации, значение o_s2 не­сколько изменяется по радиусу р в связи с ростом скорости и сте­пени деформации при уменьшении р от b до а (см. рис. 7.32). По­этому следует по существу брать среднее значение o_s2 между на­чальным o'_S2 и конечным o's2. Наиболее правильным было бы при­нимать среднее взвешенное. Но, как показал Ю. П. Глебов, к сред­нему взвешенному весьма близко подходит среднее геометрическое

O_s2 = Vo's2Cfh Vo&Osl-

При наличии упрочнения последнее учитывают при определе­нии о_ь2 по средней степени деформации.

Для возможности учета скорости деформации е_р определим последнюю:

р ^— dt '

где е_р = 2и_гЬ²р~³ [см. стр. 291, формулу (в)], поэтому р~ dt ^ZOp '

так как b и р от времени t не зависят. Но dujdt представляет собой не что иное, как скорость движения металла в приемнике, т. е. скорость выдавливания и*.

Таким образом,

• _ • 2Ь²

⁸р — ^ив „3 •

^х Скорость металла в цилиндрическом выходном участке является ско­ростью истечения.

При входе в очаг деформации, когда р = Ь,

2и_в 4и_в sin у ⁸Р⁼ ~ ⁼ D '

При выходе, когда р = а,

' — 2ы_в6² _ 4ц_вра sin у ⁸Р ~" а^{3 —} Ф

Таким образом, отношение е_ра/е_р;, = D³/d^s показывает, что влияние различия в скоростях деформации на величину сг_о2 может быть достаточно заметным.

Как было сказано в начале параграфа, ряд исследователей применили для изучения процесса выдавливания метод линий скольжения, а также метод верхних оценок. Однако следует пом­нить, что метод линий скольжения и его варианты имеют в виду плоскую деформацию, и, как говорит В. Джонсон, «поле линий скольжения в осесимметричных задачах не удовлетворяет всем необходимым условиям, т. е. условиям равновесия, неразрыв­ности, соотношениям между напряжениями и скоростями дефор­мации и др.». Вообще «существующие методы, использующие данные полей линий скольжения плоской деформации для рас­четов осесимметричных процессов, имеют ряд допущений, точ­ность которых неизвестна» [20].

Поэтому здесь мы ограничимся рассмотрением примера реше­ния плоской задачи на прессование прутка из шероховатого (т_к - k) контейнера через плоскую матрицу.

Возможное (хотя и не единственное) поле линий скольжения представлено на рис. 7.35. Поскольку трение принято максималь­ным, две ортогональные линии скольжения, граничные со стен-

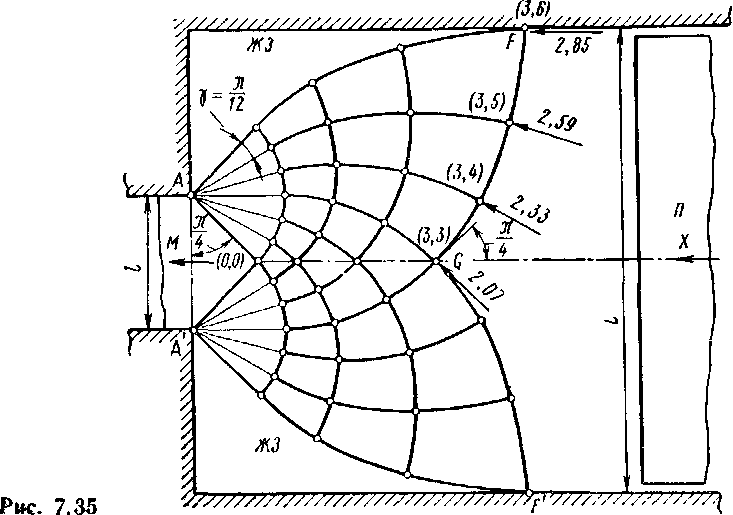
ками контейнера, пересекают стенки под углами 0 и 90°. Построен­ное поле показывает наличие жестких зон (ЖЗ) в углах контей­нера. Металл, на который воздействует пуансон П, также на­ходится в «жестком» состоянии и отделен от деформируемого ме­талла жесткопластической границей, представленной линиями скольжения F'GF. Поверхность AM А' выходящего прутка яв­ляется свободной от напряжений (трением в калибрующем пояске пренебрегаем). Усилие выдавливания определяют нор­мальные напряжения, возникающие на жесткопластической гра­нице F'GF.

Легко усмотреть, что поле, показанное на рис. 7.35, представ­ляет собой поле, построенное на дугах двух окружностей равного радиуса и притом вполне аналогичное рассмотренному на стр. 206 по рис. 6.21.

Первоначально на свободной поверхности AM А' нормальное напряжение а_х можно считать отсутствующим. Тогда в треуголь­нике АЛ' (О, 0) напряжение o_z = —2k, а в точке (0,0) среднее напряжение о₀,₀ = —k. Среднее напряжение в каждой точке жесткопластической границы GF является, в свою очередь, к ней нормальным, т. е. интегрирование напряжений вдоль линии GF даст возможность найти усилие прессования как полное, так и удельное.

Напряжения в узловых точках (3, 3)—(3, 6) легко определить по формуле (6.26), из них для точек (3, 3) и (3, 4) они уже вычис­лены в табл. 6.1 на стр. 209.

Нормальные напряжения на жесткопластической границе в ее узловых точках обозначены на рис. 7.35 в долях а* для LII я» 3,5.

Напряжение выдавливания, как правило, падает от краев контейнера к его оси. На нашем примере среднее давление со­ставляет примерно 2,3а*. Весьма точные данные для разных сте­пеней вытяжки аналитически вычислил Е. М. Макушок [46].

Эту же плоскую задачу можно решить и методом верхней

оценки. Кинематически воз­можное разрывное поле пред­ставлено на рис. 7.36, а. Пред­полагается, что пластическая область металла заключена в треугольнике 2. Годограф (рис. 7.36, б) построен обыч­ным порядком (см. стр. 216) с учетом того, что скорость истечения больше скорости выдавливания (пуансона) в LII раз, «оз/"о1 = На годографе и₀ принято за еди­ницу. Степень обжатия взята та же, что на рис. 7.35.

Удельное усилие легко определить, используя выполненные в масштабе чертежи (рис. 7.36, а я б).

Пишем уравнение баланса мощностей (см. стр. 220)

k (/20^20 ~\~ ^21^21 ~\~ ^23^2з)>

откуда

2k

Lu_nl

Подставив в полученное выражение численные значения в мил­лиметрах отрезков и скоростей, взяв их с чертежа, определим

р я* 2,8-2* = 2,8o-_s*.

Изменяя величины углов а и 9, результаты можно в какой-то мере минимизировать.