1.4.5. Скорость движения дислокаций

Дислокации движутся с определенными скоростями, величина которых для данного металла существенно зависит от величины действующих напряжений и температурных условий. Ф. Зейтц [27] приводит данные, по которым при скорости деформации L -10^_6 с"¹ для . монокристаллов чистых металлов сдвигающее напряжение, необходимое для начала пластической деформации, составляет десятые доли килограмма на 1 мм², и отмечает, что при меньших скоростях деформации в металлах наблюдается ма­лое и постепенное течение при любых сколь угодно малых на-30

Гузках. Это, очевидно, объясняется vm ■тем, что даже минимальные нагрузки _Vg при наличии тепловых флуктуации способны вызвать направленное смеще-t иие дислокаций, а следовательно., и властическую деформацию. ■ По мере увеличения напряжения влияние тепловых флуктуации на воз­можность смещения дислокаций умень­шается, и движение дислокаций, а так­же скорость их движения в основном определяются величинами действую- ^р щих напряжений.

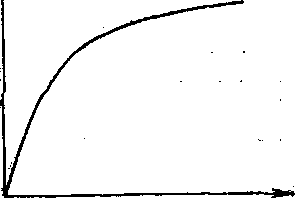
Имеющиеся экспериментальяые данные до изучению зависи­мости скорости движения дислокации от основных факторов пока ограничены [1111, однако они. показывают, что эта зависимость в первом приближении может быть представлена в виде.экспо­ненциальной функции [111]

У_дис ^=^уоехр(—-^г), . (1.2)

где .1>_явс — скорость, движения дислокации; v₀ — скорость звука в. данном металле; А — константа материала; т — действующее касательное напряжение; Т — абсолютная температура.

Схематично зависимость v_ma = / (т) при Г = const представ­лена на рис. 1.21.

Как следует из формулы (1.2), что получило и некоторое экс­периментальное подтверждение, интенсивность увеличения ско­рости движения дислокаций уменьшается по мере увеличения напряжения, а скорость движения дислокаций асимптотически приближается к скорости звука.

1.4.6. Взаимодействие дислокаций

-Как было отмечено ранее, в области дислокации атомы сме­щены из положений с минимумом потенциальной энергии, что соответствует возникновению поля напряжений, вызывающего увеличение потенциальной энергии в области дислокаций.

Силовые поля дислокаций могут взаимодействовать с сило­выми полями примесных атомов, и примесные атомы, притяги­ваются к дислокациям. Причину этого притяжения можно по­нять, рассмотрев силовое поле краевой дислокации (см. рис. ,1.11). Над плоскостью скольжения есть область сжатия, а под плоскостью скольжения — область растяжения. Атомы элемента, растворен­ного по способу внедрения, притягиваются к области растяже­ния, так как им легче разместиться среди более удаленных атомов (под дополнительной плоскостью). Атомы элемента, растворенного по способу замещения., притягиваются к области растяжения,

если их размеры больше атомов основного металла, и к об­ласти сжатия, если они меньше. Такое размещение примес­ных атомов уменьшает потенциальную энергию, так как энер гия итогового поля, имеющего место при слиянии силовых полей дислокаций и инородных атомов, будет меньше суммы энергий силовых полей, создаваемых дислокацией и инород­ными атомами.

Таким образом, в результате диффузионных процессов дисло­кации оказываются окутанными облаком примесных атомов (об­лако Коттрелла). Напряжение, необходимое для начала движе­ния таких дислокаций (для выведения их из облака Коттрелла), больше напряжения, требующегося для последующего движения дислокации. Разница в величинах этих напряжений тем больше, чем больше разница между энергией силового поля дислокации, окруженной инородными атомами, и суммой энергий силовых полей дислокации без инородных атомов и примесных (инород­ных) атомов без дислокации.

Силовые поля дислокаций могут взаимодействовать не только с силовыми полями инородных атомов, но и между собой. Так, например, разноименные дислокации (положительные и отрица­тельные), расположенные в одной плоскости скольжения, притя­гиваются (и при слиянии уничтожаются), а одноименные дисло­кации отталкиваются. Дислокации, расположенные в пересе­кающихся плоскостях, также взаимодействуют и стремятся за­нять положение, соответствующее уменьшению потенциальной энергии кристаллической решетки. В ходе длительного отжига при достаточно высокой температуре дислокации могут смещаться, образовывая узлы или трехмерную сетку с ячейками приблизи­тельно одинакового размера (сетка Франка) [111]. Объединив­шиеся краевые дислокации, «лишние» плоскости которых пере­секаются, требуют для начала движения значительно больших напряжений, чем единичные краевые или винтовые дислокации. Подобные дислокации называют «сидячими».

Наличие трехмерной сетки дислокаций в недеформированном металле создает препятствие началу смещения подвижных дисло­каций, что приводит к увеличению предела упругости монокри­сталла.

Кроме образования пространственной сетки дислокации (также с уменьшением общей энергии) могут образовывать так называе­мые стенки дислокаций, когда краевые дислокации одного знака, расположенные в параллельных плоскостях скольжения, выстраи­ваются одна под другой. Параллельные стенки дислокаций разной длины, расположенные на малом удалении друг от друга, приво­дят к разделению монокристалла на субзерна (блоки мозаики) (см. рис. 1.18). Образование стенок дислокаций, приводящее к подразделению монокристалла на субзерна — полигоны (много­угольники), называют полигонизацйей. Для выстраивания дисло­каций в стенку необходимо и движение, и переползание дислока-32 ций, а следовательно, полигонизация — термически активируемый процесс.

Увеличение плотности дислокаций в процессе деформации может приводить к тому, что часть возникших дислокаций груп­пируется, образуя новые пространственные сетки и стенки дисло­каций, приводя, в частности, к увеличению углов разориентировки блоков мозаики. Последующее движение дислокаций, образовав­ших сетки и стенки, становится более затрудненным, и в то же время сетки дислокаций и границы блоков мозаики становятся препятствиями для движения через них других (подвижных) дислокаций.

Однако не только пространственные сетки и стенки дислока­ций оказывают сопротивление движению дислокаций. Значитель­ное сопротивление движению дислокаций оказывают силовые поля, образованные примесными атомами, а также узлы пересе­чения плоскостей скольжения (вне зависимости от того, идет ли скольжение по обеим пересекающимся плоскостям или по одной из них). Последнее обстоятельство связано с тем, что в области пересечения плоскостей скольжения могут возникать угловые (сидячие) дислокации, силовое поле которых оказывает значи­тельное сопротивление смещению подвижных дислокаций.

Рост сопротивления движению дислокаций обусловлен также накоплением дислокаций одного знака у препятствий, что повы­шает энергетический потенциал в области препятствия, и рядом других причин, более детально рассмотренных в специальной ли­тературе по дислокациям [49, 57, 111] и др.

Накопление дислокаций одного знака у препятствий может подавлять деятельность источников дислокаций, что уменьшает возможность появления подвижных дислокаций.

Как было отмечено ранее, силовые поля примесных атомов являются препятствиями для движения дислокаций. Отсюда следует, что с увеличением количества примесных атомов сопро­тивление движению дислокаций, а следовательно, и сопротив­ление пластическому деформированию должно увеличиваться.

В то же время наличие подвижных дислокаций создает воз­можность последовательного смещения групп атомов в новые положения равновесия и уменьшает сопротивление по сравнению со случаем, когда скольжение осуществляется путем одновре­менного относительного смещения атомов параллельных пло­скостей (бездислокационное скольжение). Отсюда следует, что существенное уменьшение числа дислокаций и источников их появления должно повысить сопротивление пластическим де­формациям. Последнее подтверждается тем, что у полученных в естественных или искусственных условиях нитевидных моно­кристаллов («усов»), почти не имеющих дислокаций, сопротивле­ние пластическим деформациям близко к теоретическому, рас­считанному из предположения об одновременном смещении ато­мов параллельных плоскостей. Отмечается, что совершенное