7.4. Выдавливание

7.4,1. Общие положения

При штамповке выдавливанием происходит истечение металла, заключенного в замкнутую полость, через отверстие в ней, форма которого определяет поперечное сечение выдавленного участка деформированной заготовки.

Штамповку выдавливанием применяют для получения поковок с формой стержня (цилиндрического, конического, ступенчатого и т. п.) с утолщением на одном конце его. Выдавливанием получают стержневые элементы таких поковок.

Штамповка выдавливанием принципиально не отличается от процессов прессования. Последние уже давно широко распро­странены для производства прутков, профилей и труб из различ­ных материалов. Этим объясняется, что большинство исследова­ний посвящено именно процессам прессования. Основоположни­ками работ в области физики процесса прессования явля­ются Н. С. Курнаков и С. Ф. Жемчужный 143]. Ценнейшие экспериментальные и теоретические исследования проводил С. И. Губкин. Большие обобщающие работы по технологии прес­сования принадлежат П. С. Истомину.

И. М. Павлов [64] изучал влияние дополнительных напряже­ний в процессе выдавливания и создал оригинальную теорию, объ­ясняющую образование трещин (елки). Фундаментальный обоб-

287

щающий и оригинальный труд по те­ории прессования создал И. Л. Перлин 166]. Непосредственно штамповке выдав­ливанием ряд работ посвятили А. В. Ре-бельский [76] и Л. А. Шофман [121 ].

Из зарубежных исследователей успеш- но занимались прессованием X. Ункель [131], Г. Закс и В. Эйсбейн [127], Э. Зибель [28], Э. Фангмайер. Впослед- ствии к изучению процессов прессова- ния был применен метод линий сколь- жения (Р. Хилл [113], В. Прагер и Рик. 7.31 Ф. Ходж [73], А. Г. Грин и Д. Ф. В. Би-

шоп). Позже В. Джонсон, X. Кудо [20], а также Ш. Кобаяши разработали метод верхних оценок; Э. Томсен применил метод визиопластичности [106].

Штамповка выдавливанием протекает при ярко выражен­ной схеме неравномерного всестороннего сжатия, обеспечиваю­щей металлу высокую пластичность.

Штамповка выдавливанием, не отличаясь принципиально по схеме напряженно-деформированного состояния от процесса прес­сования прутков, профилей и труб, тем не менее имеет свои харак­терные особенности. При штамповке выдавливанием: 1) расстоя­ние от торца пуансона до дна матрицы в конце рабочего хода обус­ловлено заданным размером утолщенного элемента поковки, а не толщиной минимально допустимого пресс-остатка; 2) длина стерж­невой части поковки определяется ее конструкцией, но в то же время возможность выполнения стержневой части ограничена параметрами пресса; 3) поковка извлекается из штампа при обрат­ном ходе пресса при помощи выталкивателя, а не отделяется от пресс-остатка, как пруток при прессовании.

В дальнейшем будем в основном рассматривать выдавливание тел вращения, когда напряженное состояние в очаге деформации осесимметрично и схемой главных напряжений будет схема /, 7 (см. рис. 5. 12).

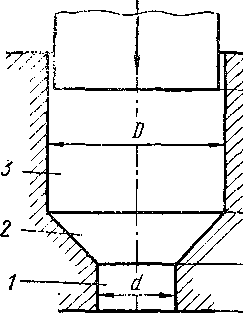
Рассмотрим простейший случай штамповки выдавливанием, когда матрица состоит из трех рабочих участков (рис. 7.31): вы­ходного цилиндрического участка 1, который калибрует стержне­вую часть поковки; заходного конического участка 2, в котором происходит основная деформация исходной заготовки и который образует переход от стержня к утолщению поковки; наконец, цилиндрического участка 3, являющегося приемником («контей­нером») исходной заготовки с размерами D и L (утолщенную часть поковки можно подвергать дальнейшей деформации на последую­щих переходах).

В соответствии с этим условия течения металла необходимо рассмотреть по всем этим участкам, в совокупности определяющим усилие выдавливания.

7.4.2. Цилиндрический выходной участок матрицы

Металл, протекающий через цилиндрическую часть матрицы, не претерпевает формоизменения. Деформирование заканчивается в конце предыдущего участка. Следовательно, по закону наличия упругой деформации при пластическом деформировании (см. стр. 62) металл в выходной цилиндрической части матрицы на­ходится в упругом напряженном состоянии. Отсюда следует, что максимальная абсолютная величина радиального напряжения о_р1 у стенки матрицы не может превзойти напряжения текучести Од¹. Фактически это напряжение меньше, поскольку матрица не яв­ляется абсолютно жесткой и сама упруго деформируется. Примем максимально возможное абсолютное значение напряжения о_р1:

Сопротивление движению металла будет создавать контактное трение, равнодействующая которого (рис. 7.31)

Pi = M-i I ^CTpi \ndl = pitr_sln dl,

а необходимое удельное усилие р на входном сечении цилиндри­ческой части матрицы

откуда окончательно получаем

Pi = o_sl^L. (7.53)

7.4.3. Конический участок матрицы

Рассмотрим этот участок, используя сферические координаты р, Ф и 6. За верхнюю границу очага деформации приближенно при­мем поверхность mfn шарового сектора с радиусом b и углом при вершине конуса 2у (рис. 7.32). Нижней границей будем считать поверхность m'f'n' шарового сектора с радиусом а, с тем же углом при вершине конуса 2у. Давление на нижнюю границу очага де­формации известно — это давление p_L; удельное усилие р₂ на верхней границе является искомым. Примем, что смещения частиц в очаге деформации происходят по радиусам р. Тогда смещения по координатам <р и 6 будут равны нулю: и_ф = и_в = 0.

Задачу решим, пользуясь методом баланса работ. Примени­тельно к данному случаю уравнение (6.40) можно написать так:

¹ В дальнейшем к обозначениям напряжения текучести a_s и коэффициента трения [г будут добавляться индексы участков, так как величины а$ и (i по уча­сткам в общем случае различны.

A₂ = A_D-\-A_rA_rA₁, (а)