7,3.2, Протяжка заготовки круглого сечения

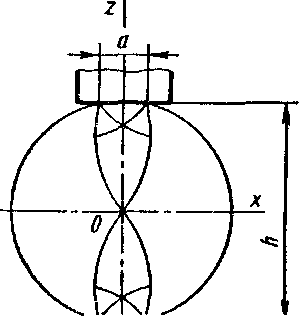
Если обрабатывать круглую заготовку плоскими бойками (рис. 7.25) при небольших обжатиях за каждый удар молота или нажим пресса, непрерывно кантуя ее после каждого удара, in можно получить заготовку меньшей площади также круглого сечения. Однако в практике ковки давно известно, что при таком способе протяжки круглой заготовки даже из, пластичной стали по ее оси образуются рыхлоты.

Это объясняется особенностями напряженного состояния кру­глой заготовки при ее обжатии плоскими бойками, которое в по­перечных сечениях круглой заготовки аналогично (рис. 7.25) напряженному состоянию в продольном сечении прямоугольной заготовки при вытяжке с малыми отношениями l₀/h (см. рис. 7.23).

Из рис. 7.25 видно, что при протяжке круглой заготовки ши­рина а поверхности контакта заготовки с бойком переменная. Чем больше обжатие, тем больше становится и отношение alh и тем меньше будет величина растягивающих напряжений на оси заготовки.

Однако для того чтобы вести протяжку плоскими бойками «с круга на круг», нельзя применять степень обжатия сколько-нибудь значительную, а вследствие необходимости в непрерывной кантовке растягивающие напряжения, направленные горизон­тально, будут совпадать с различными радиусами заготовки.

Таким образом, создается разноименная схема напряженного состояния со значительной ролью растягивающих напряжений, которая обусловливает неблагоприятные условия для проявления металлом пластических свойств (см. стр. 148).

С качественной стороны судить о распределении напряжений можно в известной мере по опытам, поставленным в условиях упругой деформации, близкой к предельной. Используя опти­ческий метод исследования напряжений, Е. П. Унксов [108] для круглого сечения получил, что как вертикально направлен­ное напряжение а_и так и горизонтально направленное о₂ в се­чении о—о (рис. 7.26, о) имеют наиболь­шее значение в центре и падают к пери­ферии, но при этом напряжение о₂ яв­ляется растягивающим.

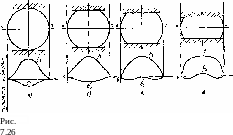
При испытании образцов со срезанны­ми параллельными фасками, что имити­рует увеличение степени деформации, об­наруживается, что величина растягиваю­щего напряжения о₂ сначала снижается по всему сечению а — а (рис. 7.26, б) вплоть до нуля в центре сечения (рис.

I■■ j —I - 7.26, в) и, наконец, это напряжение о₂

1—4-—J становится в центре сжимающим (рис.

Рис. 7.25 7.26, г). Отсюда можно с достаточной

вероятностью заключить, что и при пластической деформации опасные растягивающие напряжения в центре заготовки будут снижаться с увеличением степени деформации [108], что следует, как указано выше, и из рассмотрения поля линий скольжения (см. рис. 7.25).

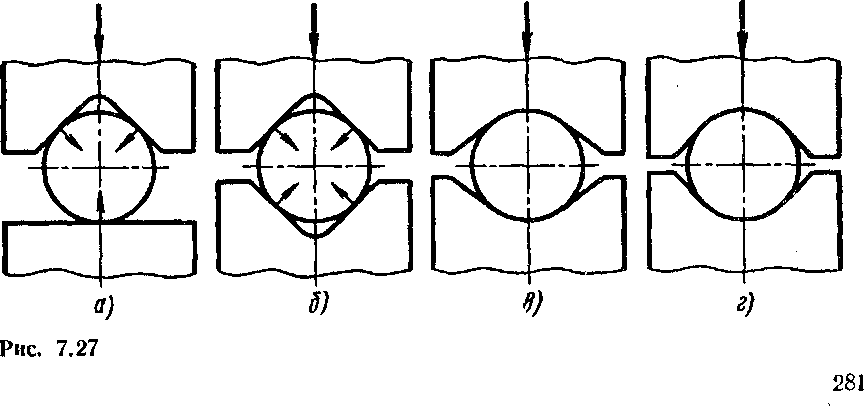
Учитывая, что при протяжке на круг плоскими бойками легко образуется осевая рыхлость даже при обработке сплавов с боль­шой пластичностью, на практике издавна избегали применять эту схему и пользовались не плоскими бойками, а бойками с вы­резом.

Из рис. 7.27 видно, что при вырезных бойках напряженное состояние будет более равномерным и в большей степени прибли­жаться к всестороннему (неравномерному) сжатию. Максимум в этом смысле, очевидно, должен быть при схеме по рис. 7.27, г. Бойки по рис. 7.27, а и б («ромбические») применяют главным образом при обкатке граней слитков, а бойки по рис. 7.27, виг — для отделки поковок круглых сечений.

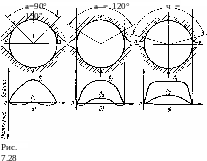Сказанное подтверждается экспериментально в предположении возможности качественной аналогии с упругой деформацией, близкой к предельной. Из рис. 7.28 видно [ 108 ], что с увеличением угла охвата напряжение а₂ в конечном итоге становится сжимаю­щим по всему сечению а—а.

Определим теперь необходимое удель­ное усилие для протяжки в вырезных круглых бойках типа г (см. рис. 7.27). Для упрощения решения рассмотрим предель­ный случай, считая, что вырез охватывает заготовку по всей окружности контура. Это будет соответствовать схеме напряжен­ного состояния 1,7 (см. рис. 5.12). При меньшем охвате удельное усилие, естественно, будет меньше. Вместе с тем учет неполноты охвата потребует дополнительных допущений.

Задача является осесимметричной, а потому примем цилиндри­ческую систему координат, расположив ось z по оси заготовки, а плоскость 0р по плоскости раздела течения металла, которая делит /₀ пополам (рис. 7.29).

Деформация е₂ не зависит от 0, так как напряженное состояние принимается осесимметричным. Будем считать ее не зависящей также и от р. Выясним относительную величину деформаций е_р и е_е. Формулы (4.4) дают

— jfcfi. _ ^дир . ^8г ~ dz '' ^еР ~ др '

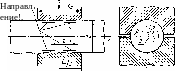Рис. 7.29

По условию постоянства объема, рассматривая деформацию в каждый данный момент, имеем

= — е,

^ёр + ^ее = - ⁶г-Тогда

ди₀ и_п 1(Г +

или

д (ри_р) —др—

— е_гр.

Интегрируя, получим

рЫ_р = - 8₂-f +/(2).

Произвольную функцию определим из условия, что на оси г, т. е. при р = 0, перемещение «_р также равно нулю. Отсюда сле­дует, что / (z) = 0, т. е. перемещение и_р, а следовательно, и де­формации е_р и е_е не зависят от z:

du,

р dp

2

(7.47)

Таким образом, мы установили, что е_р = е_е, а отсюда следует (см. стр. 141), что и Ор = о_е. Учитывая это равенство, имеем условия равновесия (3.39)

дх,

рг

дор дт₀, до ' дг

да_г . ^тгр

дг р

0;

0.

(а)

P2

Касательное напряжение т_рг на оси симметрии заготовки, т. е. при р = 0, также равно нулю, а на поверхности оно равно т_к. Считая т_р2 за линейную функцию р, получим

дх.

д₉

d

и, учитывая, что на контактной поверхности, которая нас инте­ресует, ст₂ не зависит от р и dojdz = dojdz, а р = 0,5d, по второму уравнению системы (а) получим

dz ' d

Используя условие пластичности в форме (6.11), имеем

da_z = do_p,

откуда

da_n 4_Т

На краю бойка, т. е. при z — 0,Ы₀, а_р будет таким же, как в случае отсутствия трения, т. е. при г = 0,5/₀ а_р = —o_s. Кон­тактное касательное напряжение на краю бойка принимаем т_к = = —Н^»-

Поскольку на практике при вытяжке в вырезных бойках от­ношение -j- < 2, то по аналогии с процессом осадки полосы

можно предположить, что падение касательных напряжений на контактной поверхности начнется непосредственно от края бойка к оси (в данном случае размеры 1₀ и d и координата z аналогичны соответственно размерам а и А и координате х при осадке полосы).

Поэтому изменение контактных касательных напряжений при протяжке в вырезных бойках можно представить уравнением (7.10в) (см. стр. 246), заменив в нем обозначения соответственно сказанному выше:

т_к = — 2(i_so, -j-.

Подставляя значение т_к в уравнение (б), получим dop z

откуда после интегрирования

Из условия, что при Z ную С:

С = -o_s(l

и получим окончательно

0,5/₀ о_р = —o_s, определим постоян-

2²)]. (7.48)

Деформирующую силу определим на основании интеграла (6.1), учитывая, что dF — d-dz (а_р не зависит от 6):

^{Р = 2f \o}_p^\d.dz=2'lo_s^[l₊^{^(Jl-z*)]d.dz.}

о о

После интегрирования получим

P = dl₀o_s(l +-§- ц.А). ₍7.49)

Разделив на площадь проекции контактной поверхности а7₀, определим давление:

p = cj_s(i + -fp_sA).

(7.50)

В заключение этого параграфа определим удельное усилие для протяжки в вырезных бойках б оправкой, применяемой при изготовлении полых поковок.

Схема этой операции представлена на рис. 7.30. Существенным ее отличием от предыдущей является то, что трение происходит по двум поверхностям: наружной (бойка) и внутренней (оправки). Для решения этой задачи допустим, как и в предыдущем случае, что напряжение о_г на контактной поверхности не зависит от коор­динаты р:

дг

dz

Из системы уравнений равновесия (3.39) необходимо второе уравнение, которое напишется так:

pz

dt

dp

dz

= 0.

(r)

Касательные напряжения т_рг) где-то при 0,5D > р > 0,5d, должны обратиться в нуль (рис. 7.30). Предположим, что это

D + d

произойдет на среднем радиусе заготовки при р = —j—.

Для получения условия равновесия на наружной контактной поверхности допустим, что т_рг является линейной функцией р. Тогда

~ 0,5£> — 0,25 (D -\- d) ~ D — d'

Подставляя значения

дт_ог

-д—; р=0,5Оит_р2=т_к

в уравнение (г), получим для наружной контактной поверхности

^й°г ■ 4т_к 2т_{к 0} dz ' D — d ^ D ^и-

Используем условие пластичности в форме (6.11) da₂ == dGp, и, следовательно,

dz ^ D — d ^ D • ^w

На краю бойка, т. е. при z = 0,5/₀, напряжение о_р должно быть таким же, как при протяжке с оправкой при отсутствии трения. Схема же такой операции представляет собой не что иное, как деформацию трубы с оправкой, подвергнутой внешнему рав­номерному давлению, т. е. задачу, рассмотренную ранее (см. стр. 274). Из рис. 7.21 видно, что требуемое напряжение умень­шается с увеличением толщины стенок.

На практике при протяжке с оправкой отношение Did нахо­дится обычно в пределах 1,3—3, что по рис. 7.20 соответствует значениям |а_р|, равным (1.08—l,03)o_s.

Примем некоторое среднее значение, учитывая незначитель­ную величину коэффициента, например 1,05, т. е. будем считать, что при протяжке с оправкой a_p = —l,05a_s при z — 0,5/₀.

Аналогично, как при протяжке в вырезных бойках сплошной заготовки, примем, что

т_к = — 2ц,-1,05а,

Подставляя это выражение в уравнение (d) и произведя пре­образования, получим

do_n /2 , 1 \ z г,

-4ц,• 1,05a_s (oZTJ + -о ) ~k ⁼ °-

Интегрируя и учитывая, что D — d = 2s, где s — толщина стенки, получим

а_р = 2|v l,05a_s ("f + -7J") 17 + ^C; C=-l,05a_s[l + 2fi₅ (A₊A)A]_;

o_p = - l,05a_s [ 1 + ijL (A + .1.) (A _ ]. ₍7.51)

Деформирующее усилие определяется, как всегда, равнодей­ствующей нормальных напряжений по проекции контактной по­верхности:

Р= l,05a₅/₀D [1 + ц.(А + А) А],

а удельное усилие деформирования

^{р = 1,05о, [ 1 + А ц,}₈ ^(А ₊ ^{_L.) /}₀^{] . (7.52)}

При d = 0, т. е. при s = D/2, формула (7.52) смысла не имеет, поскольку при d = 0 не может быть второй поверхности трения. Таким образом, формула (7.52) не может перейти в формулу (7.50).