
- •1 Москва 2' «машиностроение» I 19 7 7
- •Глава 1
- •1.1. Понятия о пластической деформации
- •1.2. Строение металлов
- •1 Кроме атомов, расположенных на поверхности тела, на границах зерен и внутри зерен при нарушении в них правильности кристаллического строения (см. Стр. 21).
- •1.3. Холодная пластическая деформация монокристалла
- •1.4. Элементы теории дислокаций
- •1.4.5. Скорость движения дислокаций
- •1.4.6. Взаимодействие дислокаций
- •2 М. В. Сторожев 33
- •1.5. Холодная пластическая деформация поликристалла
- •1.6. Упрочнение при холодной деформации
- •1.7. Кривые упрочнения
- •Глава 2
- •2.1. Деформация при повышенных температурах;
- •2.2. Виды деформации при обработке металлов давлением
- •2.3. Влияние температуры на сопротивление деформированию и пластичность
- •2.4. Влияние горячей деформации на свойства металла
- •2.5. Условие постоянства объема
- •2 Это так называемый закон наличия упругой деформации при пластическом деформировании.
- •2.6. Степень деформации и смещенный объем
- •3 М. В. Сторожев 65
- •2.7. Скорость деформации
- •2.8. Влияние скорости деформации на пластичность и сопротивление деформированию
- •2.9. Сверхпластичность
- •Глава 3 напряжения
- •3.1. Общие понятия
- •3.2. Напряжения в координатных площадках
- •3.3. Напряжения в наклонной площадке
- •3.4. Главные нормальные напряжения
- •3.5. Понятие о тензоре напряжений
- •3.6. Эллипсоид напряжений
- •3.7. Главные касательные напряжения
- •3,8. Октаэдр и чес кие напряжения
- •3.9. Диаграмма напряжений мора
- •4 М. В. Сторожев 97
- •3.10. Условия равновесия для объемного напряженного состояния
- •3.11. Осесимметричное напряженное состояние
- •3.12. Плоское напряженное и плоское
- •Глава 4
- •4.1. Компоненты перемещений и деформаций в элементарном объеме
- •4.2. Неразрывность деформаций
- •4.3. Скорости перемещений и скорости деформаций
- •4.4. Однородная деформация
- •Глава 5
- •5.1. Условие пластичности
- •5.2. Физический смысл условия пластичности
- •5.3. Геометрический смысл энергетического условия пластичности
- •5.4. Частные выражения условия пластичности
- •5.5. Влияние среднего по величине главного нормального напряжения
- •5.6. Связь между напряжениями и деформациями при пластическом деформировании
- •5.7. Механическая схема деформации
- •5.8. Принцип подобия
- •5.9. Контактное трение при пластическом деформировании
- •5.9.1S Особенности пластического трения
- •5,9.2. Факторы, влияющие на величину сил контактного трения
- •6 М. В. Сторожев 161
- •5.9.3. Определение касательного напряжения на контактной поверхности
- •5.10. Принцип наименьшего сопротивления
- •5.11. Неравномерность деформаций
- •1 В литературе иногда вместо термина «остаточные напряжения» применяют неправильный термин «внутренние напряжения», не считаясь с тем, что «внешних» напряжений не существует.
- •Глава 6
- •6.1. Общие положения
- •1 Интеграл (6.1) можно также записать в форме f
- •6.2. Решение дифференциальных уравнений равновесия совместно с условием пластичности
- •6.3. Основы метода расчета деформирующих усилий по приближенным уравнениям равновесия и условию пластичности
- •6.4. Метод линий скольжения
- •1 Более точные доказательства см. В работах [34, 73, из]. 7 м. В. Сторожев
- •1 Строгий вывод системы (6.22) см. В работах [33, 34, 1031.
- •2 Изложение методов численного интегрирования уравнений характеристик выходит за пределы настоящего учебника и требует от читателя знаний по математике, превышающих программу втузов.
- •6.5. Понятие о методе верхней оценки*
- •6.6. Метод сопротивления материалов пластическим деформациям
- •6.7. Метод баланса работ
- •6.8. Понятие о визиопластическом методе
- •1 Желающим изучить метод рекомендуем обратиться к литературе [102].
- •2 Примеры решений, выполненных визиопластическим методом, см. В работе [106].
- •6.9. Краткое сопоставление различных методов
- •7.1. Осадка
- •1 Здесь, как и везде в этой книге, принимается алгебраическая величина напряжений.
- •1 Берем далее абсолютные величины напряжений, поскольку знак минус для удельных усилий (средних давлений) не имеет значения, т. Е. Их можно считать всегда положительными.
- •1 Формула (7.22) приведена в [108] в другой, несколько более сложной форме. 9 м. В. Сторожев 257
- •7.2. Толстостенная труба под равномерным давлением
- •7.3. Протяжка
- •7,3.2, Протяжка заготовки круглого сечения
- •7.4. Выдавливание
- •10 М. В. Сторожев
- •7.5. Прошивка
- •7.5.2. Удельное усилие деформирования при внедрении пуансона в полупространство
- •11 М. В. Сторожен 321
- •2K Точка х
- •2 Подробнее см. В работе
- •7.7. Скручивание
- •Глава 8
- •8.1. Дополнительные данные по методике анализа
- •8.2. Гибка
- •8.3. Вытяжка без утонения стенки
- •8.4. Отбортовка
- •8.5. Обжим
- •8.6. Вытяжка с утонением стенки
- •8.7. Вырубка и пробивка
- •174, 320 Гун г. 229 Давиденков н. Н. 6 Де—Пьер в. 165
- •247, 257, 263, 280, 306 Фангмайер э. 288 Форд X. 216 Франк ф. К. 29, 32 Френкель я. И. 21 Хан в. 314
- •288, 342 Ходж ф. Р. 185, 203, 288 Христиапович с. А. 6, 185, 193
- •287, 320, 330, 358 Штэк э. 314 Эйлер л. 364 Эйсбейн в. 288 Эйхингер а, 94
7.2. Толстостенная труба под равномерным давлением
7.2.1. Общее решение
Перед тем, как приступить к рассмотрению других операций обработки металлов давлением, разберем пластически напряженное состояние толстостенной трубы под действием равномерного внутреннего или внешнего давления, поскольку решение этой задачи понадобится при рассмотрении других операций.
Эта задача осесимметричная — напряжения не зависят от координаты Э. Примем, что осевая нагрузка отсутствует, т. е. аг = 0. Поскольку рассматриваем равномерное давление, напряжения ор и ае не зависят также и от координаты z. Вместе с тем эти напряжения будут главными, так как касательные напряжения отсутствуют. Условием равновесия будет служить уравнение (3.52)
dao gp — Q~e __ _ dp р ~ U'
а условием пластичности — уравнение (5.9а), которое напишем, изменяя индексы 1 и 3 на р и Э:
2 2 2
Ор -+- о0 — арое = as.
Для упрощения решения применим метод введения новых переменных. Умножим обе части уравнения (5.9) на 4 и к левой части прибавим и отнимем 2арае. Тогда получим
ор + ае -f- 2арае -f- Зар -f- Зао — 6арае = 4о%
откуда
(^i)2+3(^)2=a?
но
°0 + 0-0
Кроме того, обозначим Ор — °е
— = о„.
Тогда
Оср -f- Зоо = а?.
(7.37)
Выразим аср и а0 через новый аргумент в виде некоторого параметрического угла ■& так, чтобы уравнение (7.37) тождественно удовлетворялось. Для этого достаточно положить
2
Ср —(?е
о-р + о-е
1
as cos
(7.38)
: a, sin #.
On =
2 VT
Из уравнений (7.38) выразим ap и ae через параметр 0:
2
/3
Je
2
(7.39)
Поскольку значения стср и a0, выраженные через параметр й по уравнениям (7.38), тождественно удовлетворяют условию пластичности (7.37), постольку подстановка значений ар и а9 из уравнения (7.39) обращает в тождество и условие (5.9) при любых значениях параметра д.
Условие пластичности, выраженное формулами (5.9) (см. стр. 130), графически представляется контуром пластичности в виде эллипса (см. рис. 5.3), следовательно, и система уравнений (7.39) определяет тот же эллипс. На рис. 7.18 около соответствующих точек эллипса проставлены значения угла 0, отвечающие соответствующим значениям ар и ае по уравнению (7.39). Подставим значения а„ и ae из уравнения (7.39) в уравнение равновесия (3.52)
+
dp
о,
6е=-$ Рис. 7.18
откуда после преобразований
^.^^-(VT-ctgd) d#.
Интегрируя, получим
In р = — (# УЗ — In sin d + С),
откуда после потенцирования, обозначая постоянную ес через В2, найдем
Таким образом, получено 156] общее решение задачи по параметру
а^= ^Та'С05(#~Т-)' (7-410а)
2
ascos (7.406)
р2== -ет^р*^- (7-40в)
Определяя в частных случаях по краевым условиям постоянную В, получим для этих случаев значения ар, ае и р в функции параметра Каждому комплексу значений ар, ое и параметра О 270
на контуре пластичности (эллипсе) соответствуют определенные точки. При этом не следует думать, что параметр совпадает с углом, определяющим положение радиуса-вектора эллипса в той или иной точке.
Рассмотрим некоторые варианты.
7.2.2, Труба под внутренним давлением
Если труба подвергается только внутреннему равномерному давлению, то на свободной поверхности при р = R (R — наружный радиус трубы) напряжение ар = 0, а напряжение ае может быть только растягивающим: ае > 0. Подставляя ар = 0 в уравнение (7.40а), получим
cos (d--jL) = 0,
2 1
откуда (в пределах 0±я) § = -уП и д = — я.
Подставляя же эти значения 0 в уравнение (7.406), увидим,
2 1
что при•& = ~y я ае < 0, а при •& = д- я ае > 0; в этом, впрочем,
легко убедиться непосредственно на рис. 7.18.
Таким образом, краевому условию соответствует параметр
#= 1— я, т. е. точка а на эллипсе пластичности (рис. 7.18).
О
Подставляя •& = ^- я и р = R в уравнение (7.40в), определим
произвольную постоянную В2:
R2 = _^=£2ехр -JL1/3-; В2 = - Ц- R2 ехр УТ и получаем
откуда
^. = _А!|Дехр_(д + ^)1/3-. (7.41)
Подстановка в уравнения (7.41) и (7.40 а и 6) различных зна-
чений определяющих —5г 1, начиная с 0= 5-я, дает
Р 6
значения Rip и корреспондирующие каждому из них значения Ор и ае. В результате получим распределение напряжений по сечению трубы, находящейся в пластическом состоянии под действием внутреннего давления.
Если принять, что р — г, где г — внутренний радиус трубы, то получим те значения ор на внутренней поверхности трубы,
271
которые необходимы для того, чтобы она находилась в пластическом состоянии. Обозначая внутреннее давление через р и считая его положительным, имеем
Р = - Ор=г.
Какие значения т) следует брать, видно из рис. 7.18. Так как
напряжение ар может быть только отрицательным, то от точки а
надо переходить в сторону увеличения абсолютной величины отри-
5
цательных значений т). Вторым крайним значением ■& будет g- п,
когда
0р = — а*; ае = — 0,5а5* и = 2,963.
При дальнейшем увеличении абсолютного значения угла О величина напряжения ар [по уравнению (7.40а) 1 будет падать, что не имеет физического смысла, так как невозможно, чтобы при дальнейшем увеличении толщины стенки требовалось меньшее давление для перевода трубы в пластическое состояние. Таким
образом, при — > 2,963 трубу уже нельзя перевести по всей
толщине в пластическое состояние. Пластическая зона окружена упругой. Следовательно, пластическому состоянию трубы под внутренним давлением соответствует участок эллипса от точки а
Уп) д° точки Ъ g-11)' ^а Рис' этот Участок
заштрихован.
 Вычисленные
значения R/r,
ар
и
ов
в
функции угла ft
представлены
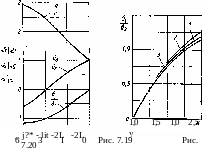
на рис. 7.19. Имея эти значения, легко
построить график напряжений ар
= —р
в
функции R/r
(рис.
7.20, кривая /).
Вычисленные
значения R/r,
ар
и
ов
в
функции угла ft
представлены
на рис. 7.19. Имея эти значения, легко
построить график напряжений ар
= —р
в
функции R/r
(рис.
7.20, кривая /).
Рассмотрим теперь задачу распределения напряжений в трубе с осевой нагрузкой и притом такой, чтобы деформация в осевом направлении отсутствовала, т. е. чтобы труба находилась в плоском деформированном состоянии.
Уравнение равновесия останется то же (3.52)
do-p ор — ое
— J- — и,
dp ' р
а условие пластичности возьмем в форме (5.18) ор — ов = ± рХ.
В нашем случае ор < о~9, следовательно, °р — 00 = - РЧ-
Подставляя уравнение (5.18) в уравнение (3.52), получим
dp р '
откуда после интегрирования ap = P<jslnpC.
При р = R Ор = 0; следовательно, Тогда
R '
Р
К In
а для внутренней поверхности, когда р —г, Ор = К In
или
р = К ln-j-.
Для плоского деформированного состояния коэффициент р = = 1,155, и кривая зависимости ар или р от отношения пройдет выше (рис. 7.20, кривая 2) кривой /, ранее полученной для плоского напряженного состояния.
Приняв же Р = 1,1 и построив кривую 3 (рис. 7.20), мы увидим, что кривые 1 и 3 весьма близки одна к другой. Поэтому для плоского напряженного состояния взамен точного решения в параметрической форме в дальнейшем можно принять [108] приближенное решение
-ор = р= 1,1<тЛп4 = l.lo.ln-^-- (7-42)
7.2.3. Труба со стержнем под внешним давлением
Рассмотрим второй вариант. Пусть внутрь трубы с внутрен ним радиусом г вставлен жесткий стержень (оправка) того же радиуса. Примем, что трение на поверхности контакта трубы и стержня отсутствует. Снаружи нагрузим трубу равномерным давлением. Спрашивается, какую величину должно иметь это дав ление, чтобы труба по всей толщине находилась в пластическом состоянии.
Очевидно, что на внутренней поверхности, т. е. при р = г, радиальное перемещение ыр отсутствует. Следовательно, тангенциальная деформация ее = ир/р — 0 [см. уравнения (4.4)]. А это значит, что внутренняя поверхность трубы будет находиться не только в плоском напряженном, но и в плоском деформированном состоянии, причем напряжение ое будет средним:
°р + ®г
и поскольку а2 = О, о - 2В.
Для определения произвольной постоянной Вг подставляем сперва ое = oJ2 в уравнение (7.406) и решаем систему (7.40а) и (7.406) относительно 0, исключая ор:
-ГаР= 7Ta'C0S(* + ir)
или
2cos(fl--^) = cos(§ + -^), откуда
В пределах 0±я этому значению тангенса соответствуют
§ = 4г и § = г-я.
о о
Удовлетворяет условиям задачи (напряжения сжимающие) 0 = = g- я, дающее при подстановке в уравнения (7.40) отрица-
274
тельные значения ор и ое. В этом можно убедиться также по рис. 7.18, где краевому условию соответствует точка Ь. Подставим
5
теперь р = г Н = —~о~п в уравнение (7.40в):
г2 = 2В2ехр В2 = — 4- ехр
51^3" 6
5 УЗ
я,
и, следовательно, получим
2
sin
д
ехр УЗ (* + -|" я)
(7.43)
Поскольку нас интересует необходимое давление р = —ар на наружной поверхности для приведения трубы в пластическое состояние, можно написать
2
sin
(7.44)
Значения О для рассматриваемого случая лежат в интервале
■ ^-п^ — л, что представляет на эллипсе пластичности (см.
рис. 7.18) участок be. р
При — = 1, т. е. когда толщина трубы стремится к 0, |ор|
достигает максимального абсолютного значения а*. При уменьшении же внутреннего диаметра абсолютное значение ор падает
и при г = 0 = оо^ снижается до os. Таким образом, изменение
вая
значений |ор| = р в функции R/r.
,1,0В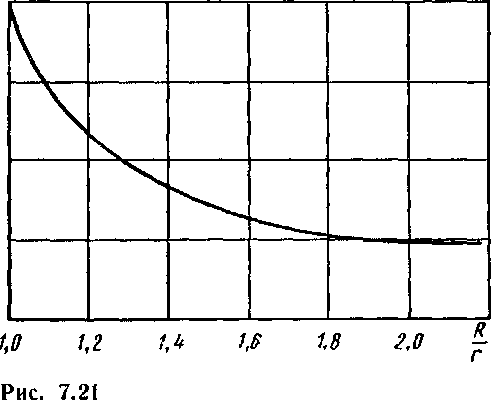 ожет
показаться несколько парадоксальным,
что при увеличении толщины стенок
наружное давление, необходимое для
приведения трубы в пластическое
состояние, падает. Однако при г = О
получается 6S
сплошной
цилиндр, дефор- 112'
мированное состояние которого
определяется де-
ожет
показаться несколько парадоксальным,
что при увеличении толщины стенок
наружное давление, необходимое для
приведения трубы в пластическое
состояние, падает. Однако при г = О
получается 6S
сплошной
цилиндр, дефор- 112'
мированное состояние которого
определяется де-
= ее,
т. е. представляет «простое растяжение»
(см. Ш
стр.
145), чему соответствует плоское
одноименное напряженное состояние ор
== ое
= —as
согласно
схеме 1,6
(см.
рис. 5.12).
1,00
