1 Берем далее абсолютные величины напряжений, поскольку знак минус для удельных усилий (средних давлений) не имеет значения, т. Е. Их можно считать всегда положительными.

На основании сказанного заменим выражение (а) следую­щим:

Р = 21

+ j — (аь — ст! ^x^) ^d* ^_ IT ^ст*^/г

0,5а ^xb

(б)

После интегрирования и подстановки значений а_ь и при веденных ранее, получим значение деформирующего усилия Р Разделив последнее на контактную площадь al, найдем у д е л ь ное усилие деформирования р:

h

^{{(■ЧГ-0+(-н--*)[1+"(т£—+)]-*}•}

(7.16)*

Последний член в фигурных скобках ц/3 отражает влияние падения касательных напряжений на центральном участке. Та­ким образом, снижение удельного давления выражается величи­ной

» h ц * 1 h

Чем больше отношение alh, т. е. чем относительно шире и ниже осаживаемая полоса, тем меньшее влияние на величину удель­ного давления оказывает наличие куполообразного участка на эпюре напряжений.

Пусть а*-4-—< O.lcTs, тогда ~г>3-!г-. Таким образом,

о а и, о

уже при отношениях > 3-5- пренебрежение участком падения

касательных напряжений вызовет абсолютную ошибку при опре­делении удельного усилия, не превышающую 10% от ст*. По­скольку же при рассматриваемом варианте всегда р > ст*, по­стольку относительная ошибка будет еще меньше. Поэтому при

отношениях -|->3-4-3,5 последний член иУЗ в фигурных скоб­ках в формуле (1.16) можно не учитывать.

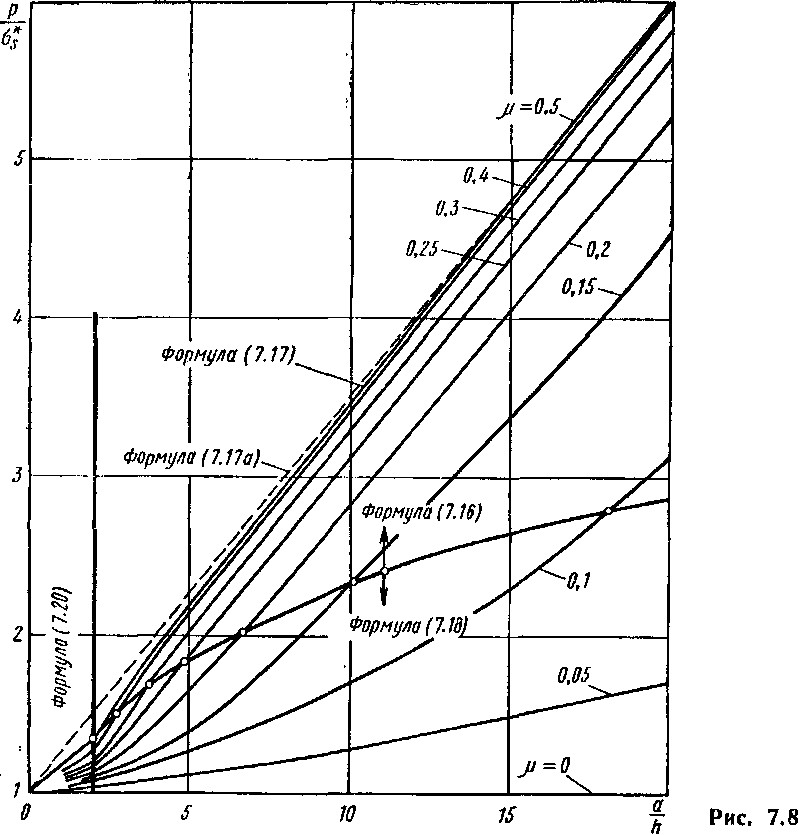
Значения р (в долях ст*), вычисленные по формуле (7.16) для разных величин коэффициента трения и., представлены графи­чески на рис. 7.8. Там же показана граница применения формулы (7.16).

2-й вариант: -|- > 2 и р. > 0,5; а_г — по формулам (7.12) и (7.11).

Р = СТс

* Формула (7.16) дана Е. П. Унксовым в другой, несколько более сложной форме, чем здесь [108, 109].

Так же как и при рассмотрении предыдущего варианта, учтем снижение интенсивности роста нормальных напряжений на цент­ральном участке площадью 0"с'0'. Тогда

"0,5а

Р = 21

(в)

j o-;(l + ^0,5\ ^xSjdx--^a_sh - о

откуда после интегрирования и деления на площадь получим [99]

^{„=„:(! +4-1-4-4). р.,?)}

Е. П. Унксов показал [ 109], что эту формулу можно получить непосредственно из формулы (7.16) для трехучастковой эпюры подстановкой li = 0,5 и ijf> = 0.

Если пренебречь в формуле (7.17) последним членом в скоб­ках, учитывающим влияние падения касательных напряжений на центральном участке, то получим [109]

р-:(^]+1т)' (^?-^17а>

Вычисление р по формуле (7.17а) даже при

а

h

= 2 дает ре-

зультат всего на 12,5% больший, чем по формуле (7.17), и состав­ляет по абсолютной величине 1/6ст*, что практически не имеет значения.

Формула (7.17а) уже была получена ранее другим методом и была отмечена как (7.26).

3-й вариант. 2 (1 + яр) > -— > 2 и 0 < li < 0,5; а₂—

по формулам (7.4) и (7.14):

(г)

откуда

Кривые, построенные но формуле (7.16) для различных зна­чений li, являются продолжением кривых, построенных по фор­муле (7.18) (рис. 7.8).

Если пренебречь менее интенсивным ростом нормальных на­пряжений a_z на центральном участке, т. е. второй интеграл в вы­ражении (г) отбросить, а первый взять в пределах 0—0,5а, то формула упростится [ 107]:

(7,19)

Расхождение результатов, вычисленных по формулам (7.18) и (7.19), тем меньше, чем больше отношение alh и чем меньше коэффициент трения ц. Однако даже при jx = 0,25 максимальная ошибка формулы (7.19) не превышает 11%.

по формуле (7.15):

откуда 1108]

(7.20)

При значении \х > 0,5 подставляется li = 0,5.

5-й в а р и а н т: при -j- < 1, а также при и. = О при любых значениях alh

Р =

(7.21)

Формулы (7.16) и (7.18) требуют для определения р в каждом отдельном случае сравнительно много арифметических подсчетов. Поэтому значительно удобнее пользоваться графиками, подоб­ными представленному на рис. 7.8.

Однако при рассмотрении графиков (рис. 7.8) легко заметить, что влияние увеличения коэффициента трения р. на удельное уси­лие сказывается резко лишь в области изменения этого коэффи­циента в пределах малых значений. При больших значениях и. (примерно от ц. > 0,25) кривые удельных усилий для разных р. стремятся к прямолинейной форме и лежат весьма близко к кри­вой для р = 0,5 [ 108]. А так как при горячей осадке величина коэффициента трения, как правило, значительна (0,3—0,5), т о для определения удельного усилия при горячей осадке без смазки в качестве ра­счетной формулы можно пользоваться фор­мулой (7.17а), выведенной для ц. = 0,5:

Эта формула дает при ц. =j= 0,5 тем большую точность, чем больше отношение alh и чем больше р. Однако даже при ц. = 0,25 абсолютная ошибка не превышает 0,3o_s* в сторону преувеличения значения удельного усилия.

При осадке с применением смазки можно рекомендовать по­лученную ранее формулу (7.2а)

(7.176)

выбирая значения фактора трения p_s по экспериментальным данным (стр. 166).

Изложенные результаты вычисления удельных усилий осадки полосы, полученные методом совместного решения приближенных уравнений равновесия и пластичности, достаточно близко совпа­дают с решениями, выполненными методом линий скольжения, в частности путем численного интегрирования уравнений харак­теристик, примененного и В. В. Соколовским.

Ранее была (стр. 204) показана возможность приближенного графического построения поля линий скольжения при осадке широкой полосы, изображенного на рис. 6.19. В центральной части полосы [треугольник (1,4) А' (4,4)] образуется жесткая зона. Она и является той зоной падения касательных напряжений (зона прилипания —- зона В), которую было необходимо логически предположить при рассмотрении процесса осадки методом реше-252

ния приближенных уравнений равновесия и пластичности (стр. 240).

Формулу (7.17а) легко получить и методом баланса работ, пользуясь уравнениями (6.40), (6.41) и (6.42) и учитывая, что при плоской деформации г_х = —е_г и 8,_; = 1,15е_х.

В последнее время некоторые исследователи для определения удельного усилия при плоской осадке применили метод верхней оценки. Однако в этом случае пользование данным методом не представляется целесообразным ни с теоретической, ни с практи­ческой стороны, поскольку при минимизации результатов послед­ние неизбежно совпадают с получаемым значительно проще ме­тодом баланса работ.

7.1.2. Осадка правильной призмы и цилиндра

Возьмем призму высотой h, имеющую в основании правильный многоугольник с числом сторон п и диаметром вписанной в осно­вание окружности d. Плоскостями, проходящими через ось при­змы и ее ребра, разделим объем призмы на п частей [96]. В соот­ветствии с принципом наименьшего сопротивления (см. стр. 166) эти плоскости примем за плоскости раздела течения. Ось z сов­местим с осью призмы, а оси хну направим, как показано на рис. 7.9.

Так как все п частей, на которые разделена призма, одинаковы и оси х, у можно расположить, как показано на рис. 7.9, в любой из этих частей, то рассмотрим распределение напряжений лишь в одной такой части ОаЬ.

Предварительно сделаем одно допу­щение: примем, что в каждый данный момент при незначительной деформа­ции форма поперечного сечения не из­меняется и треугольник ОаЬ остается треугольником.

Отсюда вытекают такие следствия:

1. 0;

   (а)

   г_х = е_у, а следовательно, о_х = о_у, что соответствует схеме V,7 (см. рис. 5.12);

2. в плоскостях, параллельных ху, касательные напряжения отсутствуют, т. е. %_ху = х_уг = 0, и имеются лишь касательные напряжения %_хг = т_гх. - При этих условиях дифференциаль­ные уравнения равновесия (3.38) при­мут вид

dz

dtxz

дх ^

Из уравнения (в) явствует, что при сделанном допущении о_и, а следовательно, и а_х = а_у не зависят от координаты у. Напря­жения о_г и %_хг будем считать также независимыми от этой коор­динаты.

Поскольку система дифференциальных уравнений (а) и (в) аналогична системе (3.50), примененной для плоской задачи, за приближенное уравнение равновесия можно принять уравнение (7.3)

чт+пг = °- <⁷-³>

Решения его, выражающие напряжение а_г в зависимости от координаты х, будут те же самые, что и для плоской задачи, с той лишь разницей, что постоянную а* необходимо за­менить на o_s, а размер а на размер d.

Для определения деформирующего усилия интегрирование будем проводить в зависимости от варианта распределения на­пряжений по участкам площади треугольника ОаЬ с умножением результата на число этих треугольников, т. е. на число сторон призмы п. Дифференциал площади dF в этом случае (рис. 7.9)

dF = 2ydx,

по

. а у = *tg — ,

поэтому

dF = 2 tg -|- х dx.

Выведем формулы,для определения удельных усилий осадки для тех же вариантов распределения напряжений, которые были при плоской задаче.

1-й вариант (три участка)

(А >2(1 +гр) и 0 < pi < 0,5) .

Пишем интеграл

^j _Ps^{exp2^ №*-*) 2tg-f-*rf* +}

Р = п

и

+ \-(о_ь-^^^) 2ig^-xdx +

ft

^{+ f — (p — 0.5o}_s ^{?'2 ~}₂^{) 2 tg -y- x dx}

_{л. jfL (\ м £*ь.\ _ J_ JЈ_\ (7.22)}

2nd² \^l -Г 3_h J 3 _d2 j.

^{После интегрирования, подстановки значений o}_b ^{и а}_с ^{и деле­ния на площадь контакта Z7 = иtg-j^ получим}

~\

где

d_b = 2x_b = 2 (0,5d — h$).

Последний член в фигурных скобках отражает влияние паде­ния касательных напряжений на центральном участке подобно аналогичному члену в формуле (7.16).

2-й вариант (два участка — Б и В) ^-^-з>2 и

(i > 0,5).

Деформирующее усилие для этого варианта

Р = п

-0.5d

Jo.(l+^pЈ)2tgЈ*d* ₊

+ | — (о_е — 0,5o_s ^h% ~ ) 2 tg * I. о J

Произведя интегрирование и отнеся к единице площади, получим [99]

'=°.(¹⁺4-4--4-£)- <⁷-²³>

Эту формулу можно также получить из предыдущей (7.22) путем подстановки в последнюю р = 0,5 и d_h = d.

Пренебрегая в формуле (7.23) последним членом в скобках, учитывающим влияние падения касательных напряжений на цен­тральном участке, получим

Вычисление р по формуле (7.24) при — = 2 дает результат

всего на 7,5% больший, чем по формуле (7.23), и составляет по абсолютной величине лишь l/12o_s. Таким образом, участок па­дения касательных напряжений здесь играет роль значительно

255

меньшую, чем в формулах для осадки полосы в условиях плоской деформации, и практического значения не имеет.

Ранее была выведена (для цилиндра) методом баланса работ формула (6.43)

I ^{1 d} p = o_s+^T_Kir.

Если в этой формуле принять т_к = 0,5а,., как это сделано в рас­сматриваемом варианте, то получим формулу (7.24). Таким об­разом, результаты обоих методов в данном случае совпадают.

3-й вариант (два участка — Л и В) [2 (1 + ^ > :> 2 и 0 < ц. < 0,5].

Деформирующее усилие

j а,exp ^2|i 2 tg+

о

Интегрируя и деля на площадь контакта f=n — tg-y, имеем

-«p-^0-¹⁺^y⁺")].

В этой формуле второй член в квадратных скобках отражает влияние падения касательных напряжений на центральном уча­стке. Однако он имеет очень малое значение, и учитывать его нет практического смысла. Отбрасывая этот член, получим расчет­ную формулу для 3-го варианта

2а_с

*² (ехр-^---^-- 1). (7.25)

а

4-й вариант (один участок В) ^ 2 и li > 0 j , Деформирующее усилие

0,5d

_{/■-» Ь[и-£(т-*}^,_)]^!!_*-г*«*-

После интегрирования и деления на площадь основания F = =- я-j-tg-rr, получим

/> = о,(1т{т). (7-26)

5-й вариант.

При и. = 0 и любых значениях dlh, а также при р ф О, но при -j- < 1

Р = cr_s. (7.27)

Формулы (7.22) — (7.27) являются общими и для правильных призм, и для цилиндра, так как при неограниченном увеличении числа сторон правильного многоугольника, являющегося осно­ванием призмы, последняя переходит в цилиндр [96].

Поскольку же поперечные сечения любой призмы в процессе ее осадки стремятся принять форму круга (см. стр. 167), постольку выведенные формулы следует считать пригодными и для проме­жуточных переходных форм поперечных сечений, образующихся в процессе осадки.

Формулы (7.22), (7.24), (7.25) и (7.26) для случая осадки ци­линдрической поковки вывел Е. П. Унксов. Он также провел обширные экспериментальные исследования, подтверждающие их правильность [108, 1091¹.

Формулы (7.22) и (7.25) достаточно сложны для вычислений. Поэтому следует рекомендовать пользоваться на практике гра­фиками. График на рис. 7.10, как и график на рис. 7.8, показы­вает, что интенсивность влияния роста коэффициента трения на удельное усилие уменьшается при увеличении его значений. Кривые для р, > 0,25 весьма близки к кривой для ц. = 0,5. Это дает возможность рассчитывать удельное усилие при горячей осадке, когда коэффициент трения большой, по приближенной формуле (7.24)

p=o_s(\ +4-4)'

Для расчета удельного усилия при осадке с применением сма­зки можно воспользоваться ранее полученной формулой (6.43), которая приведена вторично на стр. 256, положив в ней т_к =u._soy.

P = cr_s(l+f 4), (7.24а)

где \i_s, так же как и в формуле (7.176), фактор трения (стр. 165).

Эта формула широко известна под наименованием формулы Э. Зибеля [28].