1 Здесь, как и везде в этой книге, принимается алгебраическая величина напряжений.

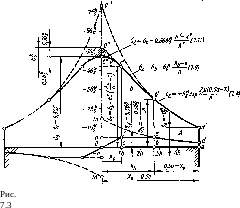
Рис. 7.3 показывает, что интенсивность роста напряжения о\, а также и т_к увеличивается к оси симметрии сечения полосы г по мере, удаления от края полосы. При этом в точке b контактной поверхности при х = х_ь касательное напряжение достигает зна­чения т_к = х_ь = 0,5а*, а напряжение о_г значения о_г = a_b ~ = 0,5а*/щ так как х_ь = ра_ь. Ближе к оси г при значениях х < х_ъ

абсолютная величина т_к, если пользоваться для о_г уравнением (7.4), получит значения, превышающие 0,5а*.

Ранее же (стр. 132) было указано, что при пластической де­формации абсолютная величина касательного напряжения не может быть больше k = 0,5а*. Отсюда следует, что предпосылка т_к = (ла_г, принятая при выводе формулы (7.4), равно как и сама формула (7.4), действительны лишь при таких значениях х, при которых | [act-, j < 0,5а* или (что то же самое) \а_г\ < 0,5a*/Li. Для этого необходимо соблюсти неравенство

2u (0,5а — х) °<^5а1 a_s ехр '- <-

h [х

Решая это неравенство относительно х, получим [108] *>0,5a+^f. (7.5)

Обозначив

^ = -гр, (7.6)

можно представить неравенство (7.5) в виде

х > 0,5а — г|)/г. (7.5а)

Таким образом, х_ь = 0,5а — tyh,

(7.7)

Вычисленные значения г|э приведены ниже [108]: [я 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,5 У 23,0 8,05 4,02 2,30 1,39 0,85 0,51 0,28 0,12 0 '

Чем больше коэффициент контактного трения, тем на меньшем участке контактной поверхности действительно выражение т_к = - p,a_s, т. е. тем скорее касательные напряжения достигают пре­дельного значения |т_к| = 0,5a_s*. При ц = 0,5 касательное на­пряжение получает это значение уже по краю заготовки в точке а, т. е. при х_ь — х_а ~ 0,5а.

В общем случае, начиная с точки Ь, касательное напряжение т_к будет оставаться постоянным, и, следовательно, для установле­ния закона изменения нормальных напряжений для значений х <• 0,5а — г|зЛ необходимо в уравнение (7.3) подставить

т„ = — 0,5а*, тогда получим

da г ^as q. dx h '

штегрируя, имеем

а_г = а*-£- + С. (7.8)

При x = x_b напряжение o_z — a_b, откуда

С = o_b — o_s •

Следовательно,

Oz = o_b — o*s ^Xb~^X . (7.9)

Таким образом, при т_к = const нормальные напряжения на контактной поверхности изменяются по линейному закону. На рис. 7.3 эпюра напряжений о_г, вычисленная по формуле (7.9), представляется прямой линией Ь'О", касательной в точке Ь' к кривой а'Ь'О". В силу симметрии к точке О" будет примыкать левая ветвь эпюры, являющаяся зеркальным отображением пра­вой.

При рассмотрении построенной эпюры напряжений (рис. 7.3) вызывает сомнение реальная возможность пересечения под углом двух ветвей эпюры на оси z в точке О". Казалось бы, что функция

239

а расстояние точки Ъ от края контактной поверхности (от точки а) (0,5а — х_ь) = #. (7.7а)

о_г и в этой точке должна быть непрерывной и иметь максимум, т. е. две ветви эпюры должны соединяться плавным переходом.

Касательные напряжения на поверхности контакта имеют разные знаки справа и слева от оси г, так как направлены проти­воположно. Таким образом, при х = 0 касательное напряжение должно перейти через 0. На эпюрах (рис. 7.3) этот переход осу­ществляется с нарушением непрерывности функции т_к, реаль­ность чего также маловероятна.

На основании сказанного возникает предположение, чт> в дей­ствительности вблизи оси г при каких-то значениях \х\ >0 начнется падение значений т_к с плавным переходом через 0 при х — 0. Если это принять, то при т_к == 0 и х = 0 из уравнения (7.3) получим

de_z _ г, dx ~~ '

а это значит, что функция о_г на оси г будет иметь экстремум, и обе ветви эпюры а, плавно перейдут одна в другую.

Предположение о наличии падения значений абсолютной ве­личины касательных напряжений на поверхности контакта при приближении к оси г подтверждается как экспериментально, так и теоретически методом линий скольжения.

С достаточным приближением к экспериментальным данным можно считать началом падения значений касательных напряже­ний точку х = х_с = h*, а законом их изменения принять

T_K = T,-f, (7.10)

где <г_е—касательное напряжение в точке х — х_с = h [1081. В данном случае

т_к = -0,5а*-!-. (7.10а)

Нормальные напряжения о_г определяются из уравнения (7,3) при подстановке <г_к из выражения (7.10а): do, * х _Л

-^-^ = 0,

откуда

о_г = 0,5а' -р- + С.

Значение С найдем из условия, что сг_г = а_с при х = х_е — h. Отсюда

* Теоретически для широкой полосы 1,29/t.

o_z = о_с — 0,5а* ^h — ^х . (7.11)

Здесь (см. кривую с'О' на рис. 7.3) о_г изменяется в пределах от о_г = о_с при х = х_с = h до а_г = а₀ = о_с — 0,5а* при х = 0. В свою очередь, по уравнению (7.9), принимая х ~ х₀ ~ h,

получим

Если бы не учитывать падения касательных напряжений, то при х = 0 получили бы по уравнению (7.9)

* ■*&

ао" = аь — а₅-^-.

Из сравнения выражений для а<г, а₀ ^{и а}с легко установить,

что

о₀- — а₀ = а₀ — а_с = — 0,5a'_s.

Таким образом, при осадке полосы эпюры напряжений, а соот­ветственно и контактная поверхность разделяются в общем слу­чае 1108] на три участка (зоны), как показано на рис. 7.3.

УчастокЛ — участок возрастания касательных напря­жений т_к или «зона скольжения» от х = 0,5а до х = х_ь = 0,5а — — г|)/г [(по формуле (7.7)].

Касательные напряжения пропорциональны нормальным на­пряжениям т₁₍ ----- \ха_г. Они изменяются от | т_к | = ра* при х = = 0,5а до |т_к| = 0,5а* при х — х_ь.

Нормальные напряжения выражаются показательной функ­цией по уравнению (7.4)

а изменяются от a_z = о_а = — а* при х = 0,5а до а_г = а_ь = = — 0,5ст*/[г при х = х_ь.

Участок Б — участок постоянства касательных напря­жений или «зона торможения» от х — x_b = 0,5а — гр/г до х = = х_с = п.

Касательные напряжения имеют постоянную величину |т_к | = 0,5at.

Нормальные напряжения изменяются по линейному закону согласно уравнению (7.9)

оь — о.

' хь — х '^s~~h~

от а_г = а_ь = —

о,5о;

при х = Х_ь

до а_г = а_с = а_ь

—:(-?-!) "р

и л;

Участокй — участок снижения касательных напряже­ний или «зона прилипания» от х — х_с = h до х — х₀ = 0.

Касательные напряжения снижаются по линейному закону (7.10а)

|т_к | = 0,5а*

от | т_к | = 0,5а₅* при х = х_с до т_к = 0 при х = 0.

Нормальные напряжения изменяются по параболической кри­вой согласно уравнению (7.11)

%

а_г = о_с — 0,5а₅ ^

от о_г = о_ь— а* - — 1 ^ при л; = х_с до а_г = ао = о_с — 0,5а* при х = 0.

Таким образом, |а₀| — |а_с| = О.^а*.

При данных размерах а и h сечения полосы при изменении величины li будет изменяться соотношение между протяжен­ностью отдельных участков.

Длина участка А, равная 0,5а — х_ь, выражается уравнением (7.7а)

(0,5а — x_b) = tyh.

При увеличении коэффициента трения р, величина гр умень­шается, становясь меньше единицы при значениях li, близких к 0,3. Следовательно, при больших величинах коэффициента трения длина участка А становится весьма незначительной, а при li = 0,5, когда \|7 — 0, участок А исчезает вовсе. В этом слу­чае эпюра напряжений о₂ состоит только из двух участков: участка Б (постоянства касательных напряжений) и участка В (их снижения).

При этом, как показывает рис. 7.3, необходимо, чтобы ширина полосы а была не менее чем в 2 раза больше ее высоты h, так как ширина участка В равна 2h, или х_с = h < 0,5а, alh > 2. Поль­зуясь рис. 7.3, легко установить, что при эпюре, состоящей из двух участков Б и В, точки а и Ъ (а' и Ъ') сливаются, и, следова­тельно,

Хь х_а ⁼⁼ 0,5aij

*. * 0,5а

о_ь = о_а= — а₅, о_с = — o_s —•

Используя эти значения, а также уравнения (7.9), (7.11) и (7.10а), получим распределение напряжений по участкам, пред­ставленное на рис. 7.4 для случая alh — 10 (так же, как и на рис. 7.3).

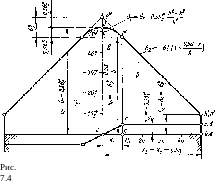Участок Б — участок постоянства касательных напря­жений от х = х_аЬ = 0,5а до х = х_с — h.

Касательные напряжения имеют постоянную величину

|т_к | = 0,5сг*.

Нормальные напряжения изменяются по линейному закону

а_г=-а;(1+-^^) (7.12)

* 0,5а

от <з_г = а_аЬ — — а₅ при х — х_аЬ до а_г = а_с — — o_s—^— при

X х_с.

Участок В — участок снижения касательных напряже­ний от х = х_с = h до х — х₀ = 0.

Касательные напряжения снижаются по линейному закону (7.10а)

|т_к | = 0,5а*—

от | т_к | = 0,5а* при х = х_с до т_к = 0 при х = х₀.

Нормальные напряжения изменяются по параболической кри­вой (согласно уравнению (7.11)1

о_г = о_с— 0,5а* ^h ~*

от а_г = а_с = — a_s до а_г =а₀= a₀--0,5as = —0,5а* + 1) ■

Вернемся к рис. 7.3. При данных значениях р. и h протяжен­ность участка А (0,5а — x_b = hty) и протяженность участка В (х_с = й) останутся неизменными при уменьшении ширины по­лосы а. Следовательно, уменьшится протяженность участка Б вплоть до того, что он исчезнет, и точки бис совпадут. То же са­мое может произойти при данном значении а, если уменьшится коэффициент трения ц,. Тогда протяженность участка В по-преж­нему будет неизменна (х_с = К), а протяженность участка А (/и|?) возрастет (\р увеличивается при уменьшении р.) за счет сокраще­ния второго участка.

Из уравнения (7.5а) легко получить [108] значение alh, при котором точки Ь и с совпадут

х 0,5а -7Г = —

Рис 7.3 показывает, что для совпадения точек b и с надо, чтобы х_ь — х_с = 0 или х_ь — h = 0, откуда х_ь = п. Подставляя это значение х_ь в уравнение (7.7), получим

-f = 2(l+i|:). (7-13)

При -^->2(1+^) эпюра напряжений состоит из трех

участков, при -Ц- <: 2 (1 + ф) — только из двух: А и В.

Эпюра напряжений из двух участков (рис. 7.5) А и В.

УчастокЛ от х — 0,5а до х — х_с.

Касательные напряжения т_к пропорциональны нормаль­ному напряжению т_к = ц.ст_г и изменяются от |т_к| = цсг* до т_к = т_с = \io_c.

Нормальные напряжения выражаются уравнением (7.4)

2ц (0,5а — х) о₂ = — o_s exp ^ -

2а (0,5а — Л) o_s exp -J^—£ ^

и изменяются от а_г = ст_а = —а* при л: = 0,5а до

О, = Ос =

при x = x_c = h.

Участок В от х = х_с = ft до х = 0.

Касательные напряжения т_к определяются уравнением (7.10):

= ^хс — = ро,

(7.106)

изменяясь от т_к = |ла_с при х = л:_с = й до т_к = 0 при л: = 0.

Нормальные напряжения получим из уравнения (7.3) при под­становке в него

*к ₊ 2ц.ст_с^ = 0, откуда

^аг = — ^цст_с -р- + ^с-

При х = и получим

h а_г = а_с. Из этого условия найдем постоянную С

(7.14)

, = h

ст_г-~а_с (l -¹- |i ^fe8 _ft2 *" ) ■

при л: = х,

На этом участке ст_г изменяется от ст_г = о до ст₀ = ст_с (1 + р-) при х = 0.

Если уменьшать дальше ширину бруса а, то будет уменьшаться

протяженность участка А, так остается постоянной и равной h. В пределе при 0,5а = h точ­ка а совпадает с точкой с (т. е. точки а, Ъ и с сольются). Таким образом, эпюра из двух участ­ков Л и /3 существует при а//г> 2, при alh < 2 эпюра на­пряжений на контактной по­верхности имеет только один участок В.

Эпюра напряжений из одного участка В (рис. 7.6).

Касательные напряжения на контактной поверхности в этом случае имеют максимальное абсолютное значение |т_к| = \ia* на краю бруса при х = 0,5а и падают в направлении оси, обращаясь в 0 при х = 0.

Закон распределения т_к определяется тем же уравнением (7.10) при подстановке в него х_с = — Lia* и замене в знаменателе h на 0,5а; так как 0,5а < h и падение напряжений идет на длине 0,5а, то

т_к = -2(ш*-^. (7.10в)

Выражение нормальных напряжений получим из уравнения (7.3) при подстановке в него указанного выше значения т_к:

da_z . * х _п

Интегрируя и определяя произвольную постоянную из условия, что при х = 0,5а а_г -— —а*, получим

*—:['+#(■?-*')]• <^7Л5>

При х = 0

а_г = -а;(1 +

Из последнего выражения видно, что чем меньше отношение alh, тем равномернее распределение напряжений по контактной поверхности.

Резюмируем ранее сказанное о возможных вариантах распре­деления напряжений.

1-й вариант. При -|- > 2 (1 + \р) и 0 < li < 0,5 эпюра

напряжений состоит из трех участков: участок А — касательные напряжения т_к пропорциональны нормальным а_г (т_к = цо\); уча­сток Б — касательные напряжения т_к имеют постоянную мак­симальную абсолютную величину (| т_к | = 0,5а*); участок А — касательные напряжения падают от максимальной абсолютной величины до нуля. Нормальные напряжения а_г определяются соответственно по участкам уравнениями (7.4), (7.9) и (7.11).

2-й вариант. При -|- > 2 и li > 0,5 эпюра напряжений

состоит из двух участков: первый участок Б — касательные на­пряжения т_к имеют постоянную максимальную абсолютную ве­личину |т_к| = 0,5а*; участок В — касательные напряжения па­дают от максимальной величины до нуля. Нормальные напря^ жения определяются соответственно по участкам уравнениями (7.12) и (7.11).

3-й вариант. При 2(l+4j5)>-^>2 и 0 < li < 0,5 эпюра напряжений состоит из двух участков: участок А — ка-246

сательные напряжения т_к пропорциональны нормальным (т_к = = lictJ; участок В — касательные напряжения падают от ца_г до нуля. Нормальные напряжения а₂ определяются соответственно по участкам уравнениями (7.4) и (7.14).

4-й вариант. При 2з>-^->1 и ц >0 эпюра напряже­ний состоит из одного участка В — касательные напряжения |т_к| падают от ц.ст* до 0; нормальные напряжения а₂ определяются уравнением (7.15).

Наконец, может быть 5-й вариант. При р. = 0 и любом alh существует один участок: касательные напряжения т_к = 0 и нормальные напряжения а_г постоянны и равны — о*.

В. В. Соколовский показал, что можно принимать а_г — —ст* также и при значении ц. > 0, если отношение -^--<1.

Зоны действия вышеперечисленных вариантов представлены на рис. 7.7 в зависимости от значений alh и (х.

Экспериментальные исследования С. И. Губкина [13, 14, 16], Е. П. Унксова [ 108], Я. М. Охрименко [63] и др. подтверждают наличие различных участков на контактной поверхности, а также в общих чертах и установленный выше характер распределения напряжений, особенно для образцов с большими отношениями alh.

Однако при экспериментах наблюдается появление вблизи краев образца дополнительных максимумов, по абсолютной ве­личине значительно меньших центрального. Кроме того, у отно­сительно высоких образцов

< 2 ч- 2,5^ наблюдаются

эпюры нормальных напряже­ний не куполообразной, а вог­нутой формы с некоторым па­дением нормальных напряже­ний от краев к оси образца. Такая форма эпюры для высоких образцов получена также теоре­тически при исследовании мето­дом линий скольжения [17, 91 и др. ].

В дальнейшем при вычисле­нии удельных усилий для вы­соких образцов ^2>-|->1^

будем исходить все же из ку­полообразной формы эпюры по 4-му варианту, поскольку по­лучаемые результаты достаточ­но оправдываются практикой р_Ис. 7.7 и весьма мало отличаются от получаемых методом линий сколь­жения.

Значения удельных усилий (средних да­влений) для различных вариантов. Зная рас­пределение напряжений а_г на контактной поверхности в пределах каждого участка и границы этих участков, можно определить де­формирующие усилия, интегрируя уравнения, выражающие а_г¹, по площадям соответствующих участков контактной поверхности, на которых они действительны, и беря сумму этих интегралов. Так как эпюры симметричны относительно оси г, эту сумму надо удвоить.

1-й вариант. При -|- 52=2(1+^) и 0 < ц. < 0,5; а_г по уравнениям (7.4), (7.9) и (7.11)

Р = 21

0,5а

j djexp

2ц (0,5а — х)

h

dx -f-

В целях упрощения последующих после интегрирования алге­браических преобразований и получения более наглядного по форме результата несколько преобразуем выражение (а).

Рис. 7.3 показывает, что второй интеграл можно взять в пре­делах не от h до х_ь, а от нуля до х_ь, вычтя при этом площадь О"с'О', которая отражает влияние менее интенсивного роста нормальных напряжений на участке В падения касательных напряжений. Третий интеграл в выражении (а) при этом отпадает.

Площадь 0"с'0', в свою очередь, представляет собой разность между площадью треугольника О"с'с" и площадью параболичес- кого сегмента О'с'с": площадь О"с'О' — 0"с'с" — О'с'с"; пло- * 2 * 1 *

щадь О"с'О' — 0,5ct_s/i g- 0,bo_sh — -g- оУ*-