1.4. Элементы теории дислокаций

Предположение о наличии дислокаций, как своеобразных нарушений закономерности расположения атомов в решетке моно­кристалла, было выдвинуто в связи с необходимостью объяснить значительную разницу расчетных и фактических величин каса­тельных напряжений, необходимых для начала пластических деформаций. Расчетные значения этих касательных напряжений превышали фактические на три-четыре порядка. Столь существен­ную разницу можно было объяснить лишь тем, что действитель­ный процесс скольжения осуществляется не одновременным сме­щением всех атомов одной кристаллографической плоскости относительно атомов смежной, параллельной плоскости, а по­следовательным смещением групп атомов, расположенных в дай­ной плоскости.

Возможность последовательного смещения отдельных групп атомов вдоль плоскости скольжения при уменьшенных напряже­ниях возникает, если дефекты кристаллической решетки являются не точечными (вакансии, лишние атомы), а линейными, т. е. вызывающими нарушения правильного расположения атомов на значительные (макроскопические) расстояния в одном направле­нии и на малые (несколько межатомных расстояний) в направле­ниях, перпендикулярных к первому.

Предположение о существовании линейных дефектов кристал­лической решетки реальных монокристаллов позволило не только объяснить причины различия расчетных и фактических величин касательных напряжений, вызывающих пластическую деформа­цию, но также выяснить многие вопросы, связанные с механизмом деформирования и явлениями, сопутствующими пластической деформации.

Появление элементов теории дислокаций относится к 20-м годам этого столетия (работы Я. И. Френкеля, Дж. Тейлора, Е. Орована и др.). Однако экспериментальное подтверждение существования дислокаций получено лишь в 50-х годах благо­даря развитию экспериментальных средств исследований строе-

ния кристаллов. Существование дислокаций было подтверждено как прямыми методами исследования (с помощью ионного про­ектора, рентгеновской топографии, <электронно-микроскопиче-ского исследования), так и косвенными методами исследования (метод ямок травления, муаровых фигур и др. [49]).

4

1.4.1. Типы дислокаций

Основными типами дислокаций, встречающихся в реальных монокристаллах, являются краевая и винтовая дислокации.

Как видно из схемы (рис. 1.11),краевая дислокация возникает, если по одну сторону от плоскости скольжения коли­чество атомных плоскостей, перпендикулярных к плоскости сколь­жения, больше, чем по другую. В случае, представленном на рис. 1.11, выше плоскости скольжения имеется добавочная плос­кость а, усеянная атомами, не имеющая продолжения ниже плос­кости скольжения. Линию в—г пересечения добавочной плоскости с плоскостью скольжения называют линией дислока­ции, а точки (й, г и др.) пересечения линии дислокации с пер­пендикулярными к ней кристаллографическими плоскостями на­зывают центрами дислокации. Условное обозначен ние краевой дислокации показано жирными линиями около центра дислокации.

Краевые дислокации условно разделяют на положительные (обозначаются _[_) и отрицательные (обозначаются Т) в зависи­мости от расположения дополнительной плоскости относительно плоскости скольжения. Краевая дислокация считается положи­тельной, если дополнительная плоскость находится выше плос­кости скольжения, и отрицательной, если дополнительная плос­кость расположена ниже плоскости скольжения.

Наличие дополнительной плоскости, ограниченной линией б—г, вызывает нарушение правильного взаимного расположения атомов, соответствующего минимуму потенциальной энергии. Наиболь­шие нарушения правильности взаимного расположения атомов возникают вблизи центра дислокации (или линии дислокации). Для положительной краевой дислокации (рис. 1.11) межатомные расстояния вблизи линии дислокации выше плоскости скольже­ния уменьшены, а ниже плоскости скольжения увеличены по сравнению с межатомными расстояниями в идеальной решетке. Эти искажения межатомных расстояний быстро убывают по мере удаления от линии дислокации. Нарушение правильности взаим­ного расположения атомов вблизи линии дислокации повышает потенциальную энергию участка кристаллической решетки вблизи линии дислокации. Таким образом, вблизи дислокации возникает силовое поле с повышенным уровнем потенциальной энергии.

Под действием сдвигающих напряжений т (рис. 1.12), дей­ствующих параллельно плоскости скольжения, краевая дис­локация способна передвигаться. Смещение дислокации состоит 22

( Направление I движения в дислокации и I пластического i сдвига

в том, что дополнительной, лишней, плоскостью поочередно становятся плоскости, параллельные исходной плоскости ab (рис. 1.12). Элементарный акт смещения краевой дислокации на одно межатомное расстояние, схематично показан на рис. 1.12. Штриховыми линиями на этом рисунке показана решетка, обра­зованная после смещения центра дислокации из положения Ь в положение Ь_х. При этом первоначальная лишняя плоскость Ьа замыкается на расположенную ниже плоскости скольжения кри-| сталлографическую плоскость be, а лишней плоскостью становится плоскость Ь_ха_х. Естественно, что пробег такой дислокации от од­ной боковой поверхности монокристалла до противоположной дает смещение части монокристалла выше плоскости скольжения относительно части монокристалла, расположенной ниже пло­скости скольжения на одно межатомное расстояние. Таким обра­зом, смещение краевой дислокации приводит к последовательному переходу атомов на плоскости скольжения в новые положения равновесия, т. е. приводит к возникновению пластической де­формации.

Как видно из приведенной схемы, направление пластического сдвига параллельно направлению движения краевой дислокации. Заметим, что одно и то же смещение одной части монокристалла относительно другой вдоль плоскости скольжения создается про­тивоположным смещением положительных и отрицательных дис­локаций.

Схема винтовой дислокации приведена на рис. 1.13. В области винтовой дислокации кристаллографические плоскости, перпендикулярные к плоскости скольжения, получают изгиб. Схематично возникновение винтовой дислокации можно пред­ставить следующим образом: часть кристаллической решетки разрезана по плоскости скольжения, и разделенные участки сме­щены один относительно другого на одно межатомное расстояние, как это показано на рие. 1.13. Образующаяся при этом зона изогнутых кристаллографических поверхностей, с обеих сторон

Рис. 1.13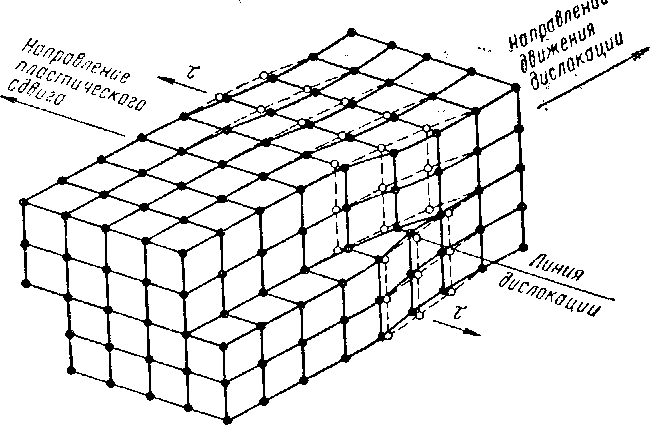

граничащая с участками, имеющими правильное кристаллическое строение, является зоной силового влияния винтовой дислокации.

Линия, находящаяся в плоскости разреза и проходящая в зоне наибольшего искажения решетки, называется линией винтовой дислокации. Движение линии винтовой дислокации в плоскости скольжения вызывает поперечное смещение атомов в новые поло­жения равновесия. Таким образом, если движение краевой дис­локации дает пластический сдвиг в том же направлении, в ко­тором движется дислокация, то движение винтовой дислокации дает пластический сдвиг в направлении, перпендикулярном к на­правлению движения дислокации.

Пробег винтовой дислокации от одной внешней границы моно­кристалла до другой вызывает смещение одной части монокри­сталла относительно другой в плоскости скольжения на одно межатомное расстояние.

Дислокация данного типа названа винтовой вследствие того, что смещенные из положений равновесия атомы располагаются в пространстве по винтовой линии. Сказанное можно пояснить рис. 1.14 [57]. На этом рисунке показано расположение атомов в двух смежных атомных плоскостях, одна из которых располо­жена в плоскости скольжения. Белыми кружочками обозначены атомы, расположенные в плоскости скольжения (см. рис. 1.13), а черными — атомы, расположенные в смежной параллельной плоскости, находящейся выше плоскости скольжения. Атомы, находящиеся в рядах от 1-го до 5-го и от 9-го до 14-го, образуют правильную кристаллическую решетку. Атомы же, расположен­ные в рядах от 5-го до 9-го, смещены из положений равновесия и располагаются по винтовой линии, схематично показанной на рис. 1.14,6, закручиваясь вокруг линии дислокации ВС. Дисло­кация, как и резьба винта, может быть правой или левой в зави­симости от направления движения по винтовой линии при пере­ходе от атомов верхнего горизонта к атомам нижнего горизонта

Рис. 1.14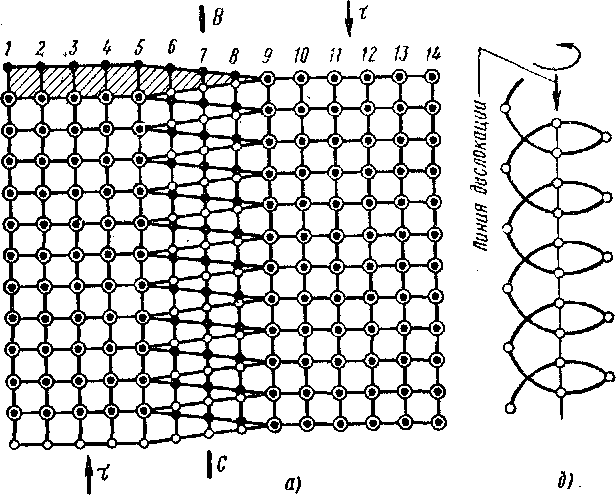

около линии дислокации. Изображенная на рис. 1.13 и 1.14 дис­локация является левой винтовой дислокацией, так как линию дислокации при движении сверху вниз следует обходить по спи­рали против часовой стрелки.

Для того чтобы движение дислокаций могло приводить к пла­стической деформации монокристалла, необходимо, чтобы линия дислокации выходила на поверхности монокристалла или же образовывала замкнутую петлю.

Замкнутые петли дислокаций могут быть составлены из крае­вых дислокаций или образованы из краевых и винтовых дисло­каций. Они могут быть замкнутыми криволинейными, когда на некоторых участках петли будут так называемые смешанные дисло­кации, при которых нарушения правильности взаимного располо­жения атомов имеют признаки, свойственные и краевым, и вин­товым дислокациям.

1.4.2. Переползание дислокаций

Краевые и винтовые дислокации могут перемещаться из одной плоскости скольжения в другую, ей параллельную.

Различают движение дислокации и переползание дислокации. Применительно к краевым дислокациям движение дислокации характеризуется смещением дислокации вдоль одной плоскости скольжения, причем размеры дополнительной атомной плоскости остаются неизменными. Переползание краевой дисло­кации дает переход дислокации из одной плоскости скольжения в другую, ей параллельную, причем размеры дополнительной плоскости изменяются за счет переноса вещества путем диффузии.

Для перехода краевой дислокации в расположенную выше соседнюю плоскость скольжения необходимо, чтобы цепочка

атомов на самой кромке добавочной плоскости ушла в глубь монокристалла путем диффузии (положительное переползание). Для перехода краевой дислокации на нижележащую соседнюю плоскость скольжения необходимо, чтобы к краю добавочной плоскости за счет диффузии присоединился один атомный ряд.

Так как диффузия есть термически активируемый процесс, то переползание также является термически активируемым про-? цессом, скорость протекания которого существенно зависит of температуры, возрастая с увеличением последней.

Переползание дислокации, связанное с изменением меж­атомных расстояний, вызывает деформацию кристаллов, а при интенсивном переползании и направленной (вследствие воздей­ствия внешних сил) диффузии атомов может являться источником возникновения пластических деформаций.

Так как винтовые дислокации не имеют «лишних» атомных плоскостей, то переползание винтовой дислокации не требует переноса вещества путем диффузии и переход винтовой дислокации на новую плоскость скольжения осуществляется сравнительно беспрепятственно.

1.4.3. Вектор Бюргерса

Для характеристики типа дислокации и степени нарушения правильности взаимного расположения атомов, вносимого дисло­кацией в идеальную решетку, удобно использовать так называе­мый вектор Бюргерса. А. X. Коттрелл [40] дает следующее опре­деление вектора Бюргерса. Допустим, что в плоскости чертежа (рис. 1.15) находится плоскость скольжения, причем на ней в об­ласти Л скольжение уже произошло, а в области В еще нет. Граница является линией дислокации. Вектор Бюргерса опреде­ляет направление и расстояние, на которое атомы в области А сместились над плоскостью скольжения по отношению к атомам, находящимся под этой плоскостью. Если модуль вектора Бюр­герса равен параметру решетки, то такая дислокация называется единичной или дислокацией единичной мощности. Из схем крае­вой дислокации (см. рис. 1.11) и винтовой дислокации (см. рис. 1.13) следует, что вектор Бюргерса для краевой дислокации перпендикулярен линии дислокации, а для винтовой дислокации параллелен этой линии. Для смешанной дислокации вектор Бюр­герса составляет с линией дислокации угол, отличный от нуля или 90°, и его можно разложить на два составляющих вектора, направленных вдоль линии дислокации и перпендикулярно ей. Разложение вектора Бюргерса на составляющие соответствует разложению смешанной дислокации на составляющие ее крае-, вую и винтовую дислокации.

Различают полные (единичные) дислокации и частичные.

Полная дислокация характеризуется вектором Бюргерса, равным по модулю расстоянию между двумя смеж-26

Рис. 1.15

Рис. 1.16

нъши атомами на плоскости скольжения в направлении сдвига.

Если представить атомы в виде шаров, то наиболее плотное их взаимное положение на плоскости скольжения может быть представлено так, как это показано на рис. 1.16. Слой атомов, расположенных выше или ниже рассматриваемого слоя с атомами А, при плотной упаковке должен располагаться так, чтобы центры шаров находились в лунках шаров А (точки В на рис. 1.16). Вектор Бюргерса Ь_х полной дислокации соответствует расстоя­нию между лунками в направлении сдвига. Однако переход ато­мов из В в В может осуществляться двойным перемещением по векторам~Ь_г яЪ₃, что требует меньших затрат энергии (требуется перекатываться через бугор меньшей высоты). Если движение дислокации дает смещение меньшее, чем ~Ь_Х, то такую дислокацию называют частичной (например, смещение по вектору Ь_г или Ь₃).

Частичные дислокации, нарушая закономерность чередования взаимного расположения атомов по слоям, параллельным плос­кости скольжения, приводят к образованию дефектов упаковки.

1.4.4. Возникновение и размножение дислокаций

В реальных монокристаллах дислокации возникают в процессе кристаллизации, а также в процессе пластической деформации.

Механизм возникновения дислокаций в процессе кристаллиза­ции из жидкого расплава разнообразен.

Дислокации могут возникать в результате срастания слегка разориентированных ветвей дендрита. Разориентировка может быть следствием наличия градиента температур, конвекционных токов и других причин. На рис. 1.17 показан простейший случай срастания двух симметрично разориентированных частей одного кристалла (а) и образования на поверхности срастания положи­тельных дислокаций (б).

Рис. 1.17

Рис. 1.18

Начальная ступенька винтовой дислокации может образо­ваться при кристаллизации под влиянием инородных атомов и посторонних примесей, а также вследствие того, что зародыши кристаллов чаще возникают на готовой подложке (например, стенки изложницы, твердые частицы, взвешенные в расплаве), форма которой отлична от формы правильного кристалла затвер­девающего вещества.

Существуют и другие варианты возникновения дислокаций в процессе кристаллизации [48, 111], но все они связаны с не­совершенством условий кристаллизации. Это несовершенство ус­ловий кристаллизации, связанное с конвекционными токами, градиентами температур, действием инородных атомов и другими причинами, приводит к тому, что реальный монокристалл со­стоит из субзерен (блоков мозаики). Блоки мозаики представляют собой стыкующиеся ячейки монокристаллов размерами порядка 10"*—10~⁶ см, имеющие сравнительно правильное кристалличе­ское строение, но повернутые один относительно другого на угол порядка 10'—20'. На рис. 1.18 показана схема мозаичной струк­туры реального монокристалла [41 ].

Дислокации возникают и в процессе пластической деформации, причем, хотя часть дислокаций выходит на поверхность моно­кристалла или взаимно уничтожается (например, слияние поло­жительной и отрицательной краевых дислокаций)* общее коли­чество дислокаций в процессе холодной деформации увеличи­вается. Так, например, А. Д. Манасевич [48] отмечает, что со­гласно теоретическим расчетам в хорошо отожженном металле число дислокаций составляет примерно 10⁸ в 1 см², а в наклепан­ном металле может достигать 10¹² в 1 см².

Механизм возникновения дислокаций в процессе пластической деформации выяснен не полностью, и существует ряд гипотез, 28

часть из которых имеет косвенное экспериментальное подтверж­дение. Наиболее обоснованной является гипотеза, объясняющая возникновение новых дислокаций наличием локальных препят­ствий движению исходной дислокации. Эта гипотеза была пред­ложена Ф. К- Франком и В. Т. Ридом [82]. Были предложены два механизма возникновения новых дислокаций.

Первый относится к случаю, когда дислокация имеет одно­стороннее защемление. Допустим, что линия ABC (рис. 1.19, а) изображает краевую дислокацию, а плоскости, параллельные плоскости CDE, — единственно действующие плоскости сколь­жения. Примем также, что отрезок АВ (край дислокации) за­креплен. Отрезок ВС может двигаться в плоскости CDE и вра­щаться вокруг точки В. При его движении во всех пройденных им областях осуществляется единичный сдвиг. Так, при переходе отрезка ВС в положение BD на площади сектора BCD происхо­дит сдвиг на одно межатомное расстояние. На остальных участках плоскости CDE скольжения нет. Полный оборот отрезка ВС дает сдвиг всей плоскости на одно межатомное расстояние.

Повторяющимся вращением отрезка ВС можно получить не­ограниченное количество единичных сдвигов. В действительности для осуществления единичных сдвигов необходимо, чтобы вра­щающаяся линия закручивалась по спирали, как это показано на рис. 1.19, б. После того, как линия в процессе вращения полу­чит форму спирали по всей плоскости сдвига CDE, за каждый пол­ный оборот спирали будет происходить единичный сдвиг. Закру­чивание линии ВС по спирали соответствует тому, что «лишняя» плоскость АВСС_г становится цилиндрической поверхностью, дающей спираль в сечениях, перпендикулярных к линии АВ. Закручивание вокруг точки В приводит к увеличению длины линии дислокации.

В юрой вариант размножения дислокаций при движении ча­стично заторможенной дислокации относится к случаю, Когда дислокационная линия закреплена с обоих концов. Это так назы­ваемый источник Франка—Рида. На рис. 1.20 приведена схема образования новых дислокаций из источника Франка—Рида [821. Плоскость чертежа на рис. 1.20 является плоскостью скольже­ния, содержащей линию дислокации DD' (рис. 1.20, а), закреп­ленную в точках D и D'. Приложенные напряжения т выгибают линию дислокации в дугу (рис. 1.20, б). Радиус кривизны за­висит от приложенного напряжения и уменьшается по мере роста последнего. Минимальный радиус кривизны получится, когда линия дислокации примет форму полуокружности.

Дальнейшее движение дислокации может приводить к увели­чению радиуса кривизны линии дислокации, что должно соответ­ствовать уменьшению напряжения т. При неизменном же зна­чении т линия дислокаций должна закручиваться вокруг to^j чек D и D'. Дальнейшее последовательное изменение формы и раз­меров линии дислокации показано на рис. 1.20, в—д. Линия дис­локации образует большую петлю, которая в результате встреч­ного движения точек тилв конечном итоге превращается в зам­кнутую петлю дислокации и новую дислокацию DD', аналогич­ную исходной. При встрече сегментов в точках тип они анни­гилируются, так как в этих точках дислокация имеет положи­тельную и отрицательную краевую ориентацию.

Описанные источники появления дислокаций в процессе пластической деформации не являются единственно возможными. В частности, при деформировании поликристалла дислокации могут зарождаться у границ зерен вследствие местного «надавли­вания» соседних зерен, имеющих неправильную форму, в про­цессе их формоизменения.

Появление новых дислокаций в процессе пластической де­формации и направленное перемещение их от одного края моно­кристалла к другому под действием внешних сил приводит к тому, что относительное смещение отдельных элементов монокристалла в процессе пластической деформации намного превышает меж­атомные расстояния.