3.11. Осесимметричное напряженное состояние

Одним из частных случаев объемного напряженного состоя­ния, весьма часто встречающимся при обработке металлов давле­нием, является осесимметричное напряженное состояние.

Под этим видом напряженного состояния подразумевается напряженное состояние тела вращения, к поверхности или части поверхности которого приложены распределенные нагрузки, рас­положенные симметрично относительно его оси и одинаковые во всех меридиональных сечениях (рис. 3.11). Примерами могут служить осадка цилиндрической заготовки, ее прошивка, выдав­ливание (прессование), волочение и др.

При рассмотрении осесимметричного напряженного состояния весьма удобно пользоваться взамен декартовых цилиндрическими координатами, в которых положение любой точки А определяется радиусом-вектором р, полярным углом 0, отсчитываемым от ;>си р (х), и аппликатой г, как представлено на рис. 3.12, где а — проекция точки А на плоскость, перпендикулярную к оси г,

i I I i I.

I tit I

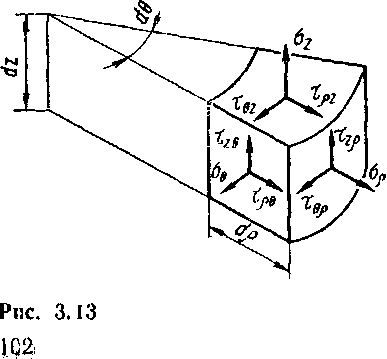
проходящую через точку О. Обозначения напряжений в цилиндри­ческих координатах и форма элемента показаны на рис. 3.13. Тензор напряжений в цилиндрических координатах запишется так:

¹рй

¹бр

¹гр ¹гв °!

Напряжение а_р называют радиальным, а₀ — тангенциаль­ным, а а₂ — осевым.

При осесимметричном напряженном состоянии компоненты напряжений не зависят от координаты 9, и, следовательно, все производные по этой координате в дифференциальных уравне­ниях равновесия обратятся в нуль. Кроме того, в меридиональ­ных плоскостях (плоскостях, проходящих через ось г, т. е. пло­скостях 0) не могут возникнуть касательные напряжения вслед­ствие симметричности тела и симметрии внешней нагрузки.

Поэтому с учетом закона пар­ности касательных напряжений

^тр9 ^{= т}ге — ^тер ~ ^тег ⁼ 0. Следо­вательно, напряжение а_в всегда будет главным, т. е. а₀ = а_2> a ось р может иметь любое направ­ление в плоскости г (т. е. в пло­скости, нормальной к оси г).

Таким образом, компоненты напряжений при осесимметричном напряженном состоянии можно записать так:

Рис. 3.14

о_р 0 т_р;

О Og О

т_гр О а_г

рг

Всего будет три нормальных и два равных между собой каса­тельных напряжения.

Применяя тот же метод, который был использован при рас­смотрении объемного напряженного состояния в декартовых коор­динатах (стр. 100), выведем дифференциальные уравнения рав­новесия в цилиндрических координатах для осесимметричного напряженного состояния.

Действующие напряжения показаны на рис. 3.14. Ось р, как сказано ранее, можно провести в любом направлении на плоскости г. Для удобства вычисления на рис. 3.14 эта ось про­ведена так, что плоскость pz является плоскостью симметрии выделенного элементарного объема.

Площади элементарных площадок

F_p = пл. abed — pdQdz;

F(p+dp) = пл. a'b'c'd' = (р + dp) dQ dz;

F_Q = пл. a'd'bc = dpdz;

F_z = пл. a'cdb' = пл. ас'd'b = p dQdp.

Запишем условия равновесия, проецируя все действующие

на элемент силы на оси риг, принимая I sin =

• а_рр аЪ dz + {о₉ + dp) (р + dp) аЪ dz — о_е dQ dp dz —

• т_ргР dQ dp -f (т_р2 + dz) p dQ dp = 0;

(a)

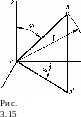- x_!PpdQdz + (т_гр + igL dp) (p + -f dp)dQdz— o₂pdQdp -f ^а_г -j-

dz

da.

dz) p dQ dp = 0.

0;

0₀

После алгебраических преобразований и сокращений, пренебрегая бесконечно малыми высших порядков, получим

dz

да.

два

др

dz

= 0.

(3.39)

При решении некоторых осесимметричных задач в дальнейшем придется встретиться кроме цилиндрических координат со сфе­рическими. В этой системе (рис. 3.15) положение точки опреде­ляется радиусом-вектором р и двумя углами 9 и ср, определяю­щими его положение в пространстве. Угол ф отсчитывается от оси г (аналогичен географической широте), а угол 9 отсчитывается от некоторой оси в плоскости, нормальной к оси z и проходящей через центр О системы (аналогичен географической долготе). Обозначения напряжений в сферических координатах получим, заменив индекс z в обозначениях, данных для цилиндрической системы, индексом ср.

При осесимметричном напряженном состоянии напряжения не зависят от координаты 9, а касательные напряжения, содер­жащие в индексе эту координату, т. е. т_р9 = т_0р и т_ф8 = т^, равны нулю.

Дифференциальные уравнения равновесия для осесимметрич-ного напряженного состояния в сферических координатах при­ведем без вывода:

дтрф J

+ — [2а_р - (о„ + о„) + t_w ctg ф] = 0;

др ~^г Р дх.

Р <Эф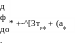

o_e)ctgcp] = 0.

(3.39a)