3.6. Эллипсоид напряжений

Выразим компоненты напряжений в наклонной площадке формулами (3.8)

S₁ = Oi^i! S₂ — 0₂fl2> S₃ ⁼ °з^аз> откуда

o2 c2 o2

2 °1 2 ^J2 2 ^З

of oi, ol

no

a\ + a\ -f a\ = 1.

Подставляя в последнее уравнение значения а² из предыду­щих выражений, имеем

(3.18)

o_lt djHo₃ для каждого данного напряженного состояния являются постоянными. Уравнение (3.J8) является уравнением трехосного эллипсоида, полуоси которого представляют ссбой главные на­пряжения в данной точке, а координаты точек поверхности— проекции полного напряжения S для различных наклонных площадок. Следовательно, длина любого отрезка от центра дд пересечения с поверхностью эллипсоида (радиуса-вектора) пред ставляет собой полное напряжение S в какой-то наклонной пло­щадке. Эллипсоид этот называется эллипсоидом напряжений (эллипсоидом Ламе) и как бы отражает геометрически тензор напряжений.

Поскольку длина радиусов-векторов эллипсоида ограничена длиной его большой полуоси с одной стороны и малой — с дру­гой, постольку полные напряжения S в различных площадках данной точки по абсолютной величине всегда меньше наибольшего (по абсолютной величине) главного напряжения и больше наи­меньшего.

Если два из трех главных нормальных напряжений равны между собой по абсолютной величине, то эллипсоид напряжений превращается в эллипсоид вращения.

Если все три главных нормальных напряжения равны между собой и одинаковы по знаку, то эллипсоид обращается в шар и любые три взаимно перпендикулярные оси становятся глав­ными. В этом случае во всех наклонных к осям координат пло­щадках действуют одинаковые равные между собой нормальные напряжения, а касательные отсутствуют [104], поскольку любая плоскость — главная. Иначе говоря, точка находится в состоя­нии равномерного всестороннего растяжения или сжатия. Тен­зор напряжений будет

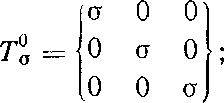
(3.19)

этот тензор напряжений носит название шарового тензора. Он ин­вариантен к выбору системы координат.

Если одно из главных напряжений равно нулю, то эллипсоид превращается в эллипс и объемное напряженное состояние пре­вращается в плоское. Наконец, если два главных напряжения равны нулю, эллипсоид превращается в отрезок прямой линии, что соответствует линейному напряженному состоянию.

3.7. Главные касательные напряжения

Касательные напряжения в наклонных площадках, если тен­зор напряжений дан в главных компонентах, выражаются урав­нением (3.11)

т² = о\а\ -|- olal -f- oiai — (о^а² -\- о₂а\ + а₃аз)².

Выясним, в каких площадках касательные напряжения полу­чают экстремальные значения. Из условия

а\ + а\ -f а\ = 1 (^а>

2 1 2 2

а₃ = 1 —cti — ai.

имеем, например,

'-*2

Подставляя а\ в выражение (3.11), получим <г² = а\а\ А- а\а\ -f. о₃ (1 — а\ — а\) —< — [dai + o_afl^ -f о₃ (1 - o'i — а²₂) ]².

Дифференцируем по а_х и приравниваем частотную производ­ную нулю для нахождения экстремума:

ЦО- = 2а²а! — 2о1а_х — 2 [опа? + а₂а²

+ аз(1—а² —02)1(20,01 —2а₃а0 =0.

Сокращаем на 2 (Oj — a₃) и выносим а_х за скобки: ai (ai -f- а₃— 2a_tai — 2а₂аз — 2а₃ + + 2а₃а² + 2а₃а²) = 0.

Меняем знак, выносим за скобки о? и а² и делим на 2:

ai [{ai — аз) а\ -f. (о₂ — a₃) al f ^— ] ^ °- ^

Аналогичным образом дифференцируя уравнение по а_% и приравнивая частную производную нулю, получим

а₂ [ (от — a₃) а² + (а₂ — а₃) «2 §- (^аз — о"з) ] = 0. (в)

Решениями уравнений (б) и (в) прежде всего являются а_х = 0; а₂ = 0. Подставляя а_г = а₂ = 0 в условие (а), найдем а₃ == ±1 и, таким образом, получаем первую группу значений направляющих косинусов, при которых т имеет экстремум:

а_х = 0; а₂ = 0; а₃ = ±1.

Далее, приняв a_t = 0 из уравнения (в), получим а₂ — '\» а при этих значениях а_х и а_% из условия (а) определим соответ­ствующее значение а₉ = =t|/^-i- и, следовательно, получим вто­рую группу значений а_и а₂, a_s, определяющую экстремум для т:

а_{1 =} 0; а₂=_±]/2-_; а₃=±|А

2 *

Наконец, подставляя а₂ — О в уравнение (б), получим а_х — — =ь j/~-i-, а по этим значениям из уравнения (а) определим

а₃ = ± ~\f ~y и в результате найдем третью группу значений а_ъ а₂, я₃, при которых т имеет экстремум:

Далее из условия а\ + ац + аг = 1 выражаем «2 и ai, под­ставляем их значения в формулу (3.11) и производим аналогич­ные выкладки.

В результате получим следующие шесть групп значений направляющих косинусов, при которых касательные напряжения получают экстремальные значения:

		Группы значений направляющих			косинусов
Направляющие косинусы	1	2	3		5	6
«1	0	0	± 1	0
02	0	±1	0		0
а3	± 1	0	0			0

Первые три группы значений направляющих косинусов опре­деляют координатные плоскости, которые при рассмотрении дан­ного вопроса приняты за главные и в которых касательные напря­жения равны нулю. Следовательно, вторые три группы значений определяют плоскости, в которых касательные напряжения дости­гают максимальных значений (абсолютных), поскольку нахожде­ние экстремальных значений проводилось для т² по уравне­нию (3.11).

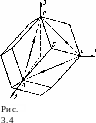
Легко видеть, что каждая из этих групп значений выражает плоскости, параллельные одной из координатных плоскостей и составляющие углы 45° с каждой из двух других, или, что то же самое, плоскости, проходящие через одну координатную ось и делящие угол между двумя другими пополам. Таким образом, всего получим (рис. 3.3) три пары (а, бив) взаимно перпенди­кулярных площадок, в которых касательные напряжения дости­гают максимальных абсолютных значений. Из шести этих пло­щадок и шести им параллельных можно составить фигуру ром­бического додекаэдра (двенадцатигранника) согласно рис. 3.4. 88

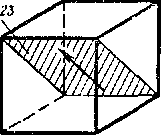
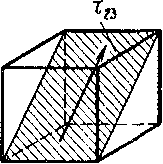
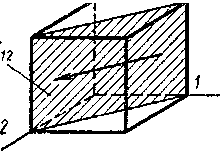
Рис. 3.3

	3
I3

Подставляя в уравнение (3.11) полученные значения направ­ляющих косинусов, найдем значения максимальных касатель­ных напряжений:

T-IO —

\

^fx.

а, =

а„ = 0

"о" (^а2 - 0Г₈)

^аг = 0. о₂

а, = ±

_V-

(3.20)

0,

Индексы при т означают, полу­разность каких главных напряжений равна данному тик каким осям плоскость действия т наклонена под углом 45° (см. рис. 3.3). Эти каса-|ельные напряжения называют так-/ке главными касатель­ными напряжениями.

Таким образом, главные касатель­ные напряжения равны полуразно-i тям соответствующих главных нор­мальных напряжений.

Наибольшее касательное напря­жение равно полуразности алгебраи­

чески наибольшего и наименьшего главных нормальных на­пряжений.

Если все три главные нормальные напряжения равны между собой, то их полуразности и, следовательно, все касательные напряжения обращаются в нуль, т. е. отсутствуют. Этот резуль­тат мы получили и раньше при рассмотрении эллипсоида напря­жений и шарового тензора (3.19).

Направления главных касательных напряжений на площад­ках их действия параллельны той главной координатной пло­скости, к которой данная площадка является нормальной (см. рис. 3.3). Вместе с тем направления главных касательных напря­жений (на рис. 3.4 показаны стрелками) образуют ребра пра­вильного октаэдра с вершинами ABC на главных осях.

Как видно из уравнения (3.20), сумма трех главных касатель­ных напряжений равна нулю:

т_1Я + т₂₃ + т₃₁ = 0. (3.21)

Из этого уравнения следует, что знак наибольшего по абсо­лютной величине главного касательного напряжения противо­положен знаку двух других.

Это условие необходимо соблюдать при назначении знаков главных касательных напряжений в каждой конкретной задаче.

На гранях додекаэдра (см. рис. 3.4), пересекающихся в точке D, т. е. в точке, расположенной в первом октанте, направления, по которым главные касательные напряжения положительны, указаны стрелками.

Определим значение нормальных напряжений в площадках, по которым действуют главные касательные напряжения, для чего подставляем значения направляющих косинусов в уравне­ние (3.10):

^{0"i2 = \ (of! + о}_г^{); а}₂₃ ^{= -i- (а}_а ^{+ а}₃^{); а}₃₁ ^{= ~ (а}₃ ^{+ а}_г^{), (3.22)}

т. е. нормальные напряжения, действующие в площадках главных касательных, равны полусуммам главных нормальных напряжений.

Из выражений (3.20) главных касательных напряжений также видно, что при увеличении или уменьшении главных нормальных напряжений на одну и ту же величину значения главных каса­тельных напряжений не изменятся, т. е. добавление к напря­женному состоянию равномерного растяжения или сжатия не изменяет величины касательных напряжений. Это дает возмож­ность всегда представить тензор напряжений в виде суммы двух тензоров.

Обозначим среднее нормальное напряжение через а_ср, тогда

_{ст =} стт + ^ff2 + q₃ _ °х + <зу + <3г^ (3.23)

т. е. среднее нормальное напряжение равно одной трети первого инварианта тензора напряжений (3.15). Составим шаровой тензор (3.19):

¹ о

[К — о_ср)

(3.24)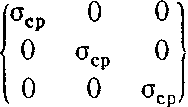

пли

Т₀ = Tl + D_a

(3.25)

Тензор D_Q называется девиатором напряжений. Таким образом, в общем случае тензор напряженного состояния определяется суммой шарового тензора и девиатора напряжений.

Легко видеть, что сумма компонент девиатора напряжений по главной диагонали равна нулю:

(о* — о_ср) + (о — о_ср) + (о_г

р) = 0.

(3.26)

Как уже было сказано (стр. 86), напряженное состояние, определяемое шаровым тензором, представляет собой всесторон­нее равномерное сжатие (о отрицательно) или всестороннее рав­номерное растяжение. Такое напряженное состояние не может вызвать изменения формы тела — возможно лишь изменение объема (при упругой деформации) и разрушение. Если же напря­женное состояние, в котором находится какое-либо тело, опре­деляется девиатором, то тело изменяет форму без изменения объема даже при упругом деформировании.

Разложение тензора напряжений на два — шаровой и девиа-гор — представляет прежде всего математическую операцию, которой не следует придавать безоговорочно физического смысла, г. е. например, считать, что тело находится под. одновременным или последовательным действием двух независимых систем напря­жений, эффекты которых складываются.

Вопрос о физическом смысле тензорных представлений в тео­рии напряженного состояния подробно рассматривал И. М. Пав­лов [65].