3.5. Понятие о тензоре напряжений

Ранее было установлено, что напряженное состояние точки выражается поверхностью (3.7). Это значит, что напряженное состояние есть величина тензорная в отличие от скалярной (опре­деляемой числом) и векторной (определяемой числом и направ­лением). Эта поверхность, а вместе с ней и напряженное состоя­ние определяются девятью напряжениями в координатных пло­щадках. Поэтому можно дать особый смысл матрице (3.1), которой были представлены эти напряжения, а именно записать

(3.12)

Правая часть равенства представляет собой g точки зрения тензорного анализа симметричный тензор 2-го ранга. Эту запись можно понимать так: напряженное состояние Т_а данной точки равно тензору напряжений с такими-то компонентами (о и т яв­ляются компонентами тензора напряжений). Так как касатель­ные напряжения попарно равны между собой и равные касатель­ные напряжения располагаются в матрице симметрично отно­сительно главной диагонали (а_х, а_у, о_г), то возможна сокращен­ная запись

(3.12а)

Если даны главные напряжения, то тензор напряжений запи­шется так:

(3.126)

С тензором можно производить различные математические действия, изучаемые в тензорном анализе, в частности тензоры можно вычитать и складывать, с чем мы встретимся дальше.

Выясним теперь, можно ли определить величину главных напряжений и положение главных плоскостей по тензору напря­жений, данному в произвольных координатных осях.

Пусть в какой-то, пока неизвестной, наклонной площадке действует только нормальное напряжение а, т. е. эта площадка является главной. Пусть положение этой площадки определяется направляющими косинусами а_х, а_у, а₂ по отношению к взятой системе координат. Тогда компоненты напряжения о по коорди­натным осям будут аа_х, аа_у, аа_г, так как направление а совпа­дает с нормалью к площадке.

Пользуясь известными выражениями (3.3), можно написать аа_х = а_ха_х + х_хуа_у -\- х_хга_г\

oa_y^=x_yxa_x-\-o_ua_y-\-x_gza_z\ , (_а)

оа_г = т_ма, + %_zya_y + а_га_г. ,

Преобразуем написанные уравнения так:

(о_х — о) а_х + т_ада_в -f- x„a₂ = 0;

V^Q* + (<у_у — о) а_у + т^а_г = 0;

+ ^zfiy + (о, — о) а, = 0.

Полученная система уравнений относительно а_Л, а_г яв­ляется линейной и однородной (свободные члены равны нулю). Так как а_х, а_у и а_г не могут быть все три одновременно равны нулю, то, как известно из теории уравнений, определитель этой системы должен быть равен нулю, т. е.

V ^ау~° V =0. (3.13)

^xzx i_zy а_г — о

Развертывая определитель и производя преобразования, полу­чим кубическое уравнение относительно а:

а³ — о² (а_х + o,j + о _г) +

+ о- (о_хОу 4- о_уо_г 4- а₂о_х — т²_у — х\_г — т²*) —

— (а_ха_уо_г 4- 2т_адt_vzt„ — oyr²^ — а^т², — о_?х\_у) = 0. (3.1 За)

Это уравнение имеет три корня, представляющие значения а_х, а₂ и а₃, которые по характеру уравнения всегда будут действи­тельными. Написав дополнительно известное из аналитической геометрии условие, что

а1 + а²_у + а²_г= 1, (3.14)

можно определить и значения направляющих косинусов пло­щадок действия главных напряжений, как это следует из условия, принятого при составлении системы уравнений (а).

При выводе уравнения (3.13а) для определения величины главных напряжений оси координат были выбраны произвольно. Главные же напряжения при данном напряженном состоянии имеют единственные значения. Отсюда следует, что коэффициенты кубического уравнения (3.13а) имеют одни и те же значения независимо от того, как были выбраны оси координат. Они не изменяют своей величины при изменении положения координат­ных осей. Иначе говоря, эти коэффициенты инвариантны к пре­образованию координат. А так как эти коэффициенты составлены из компонент тензора напряжений, то они являются и его инва­риантами при преобразовании координат. 84

линейный:

(3.15)

(3.16) const. (3.17)

Первый инвариант i_t тензора напряжений h = Gx + a_y + a, = ^const. Второй инвариант i₂ — квадратичный:

*2 = ОхОу + ОуОг + O_zO_x — Тад — %% — Т_гх = COnst

Третий инвариант i_a — кубический:

10 ^{2 2} 2

'3 ⁼ 0_XOyO_Z ""j— ^Х_ХуХу_гХ_гХ OjjTyj 0(/Т_гл; О_гТд;_(у

*ху

+

и =

(3.16а)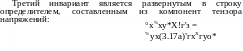

Второй инвариант является суммой миноров этого определи­теля при разложении его по главной диагонали:

а, х_г_

+

О,

Инварианты тензора напряжений имеют весьма важное зна­чение, так как они характеризуют напряженное состояние неза­висимо от выбранной системы осей координат. Так, например, если написаны два тензора, то, пользуясь инвариантами, мы сразу можем определить, выражают ли они разные напряженные состояния или представляют собой одно и то же напряженное состояние при разных осях координат.