Глава 3 напряжения

3.1. Общие понятия

Тело, подвергающееся действию сил, находится в напряжен­ном состоянии. Внешние силы, действующие на тело, бывают двух основных видов: поверхностные и объемные (массовые).

К поверхностным силам относят силы, прило­женные к поверхности тела. Они могут быть сосредоточенными и распределенными.

К объемным силам относят силы, действующие на все материальные точки тела и пропорциональные их массам, например силы тяжести, силы инерции и др. В дальнейшем дей­ствие объемных сил рассматривать не будем.

При изучении напряженного состояния принимаем, что тело однородно, изотропно и представляет собой систему непрерыв­ных материальных точек. Если система точек находится в равно­весии, то принимается, что внешние силы уравновешиваются так, как если бы система отвердела. Это так называемый принцип отвердения.

При упругом состоянии равновесие может существовать при разных соотношениях внешних сил.

При пластическом равновесии соотношения и величины сил должны быть вполне определенны, как это будет показано в гл. 5.

Под действием внешних сил в теле возникают внутренние усилия. Предел отношения внутреннего усилия АР, действующего на какую-либо элементарную площадку, выделенную в рассма­триваемой точке тела, к ее площади AF при неограниченном уменьшении последней называется напряжением S:

Каждая точка в напряженном теле находится под действием всех ее окружающих точек, а поэтому в любой плоскости, прове­денной через данную точку, на нее будет действовать напряжение, характеризуемое определенной величиной и направлением.

Полное напряжение по правилу параллелепипеда всегда можно разложить на три: одно нормальное и два касательных. В равной мере полное напряжение можно разложить на три по направле­ниям осей координат.

3.2. Напряжения в координатных площадках

Проведем через напряженную точку А (рие. 3.1) три плоско­сти, параллельные плоскостям координат. Для того чтобы иметь возможность обозначить на чертеже напряжения, действующие на точку в этих плоскостях, построим параллелепипед, ребра которого примем бесконечно малыми, неограниченно прибли­жающимися к точке. Тогда на гранях такого элементарного параллелепипеда, проходящих через точку Л, можно изобразить векторы напряжений, действующих на точку в трех взаимно пер­пендикулярных плоскостях (координатных площадках). При этом напряжение в каждой площадке разложим на три: одно нормальное и два касательных, которые направим параллельно осям координат. Таким образом, всего получим три нормальных и шесть касательных напряжений.

Нормальные напряжения в координатных площадках обозна­чим о, касательные т. Примем индексы из двух букв. Первая буква будет указывать ту координатную ось, по направлению которой действует напряжение, а вторая—ту координатную ось, которая нормальна (перпендикулярна) той площадке (внешняя нормаль), к которой напряжение приложено (адрес напря­жения). Например, т_ху — касательное напряжение, действую­щее параллельно оси х на площадку, перпендикулярную к оси у, т. е. на площадку, параллельную плоскости xz. Поскольку для нормальных напряжений направление и адрес совпадают, при­меним для их обозначения индекс из одной буквы, например а_х вместо а_хх.

Напряжения, действующие в точке по площадкам, параллель­ным плоскостям координат, геометрически изображены на рис. 3.1 стрелками.

Нормальные напряжения считают положительными, если они стремятся вызвать растяжение.

Знак касательных напряже­ний зависит от знака и направле­ния нормального напряжения в рассматриваемой грани элемен­тарного параллелепипеда.

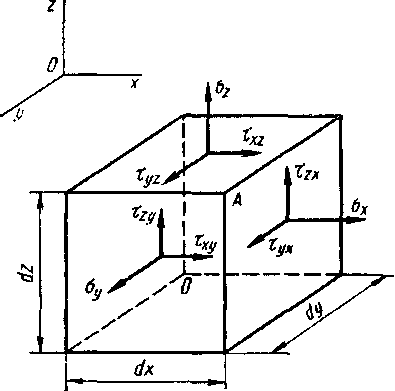
Касательные напряжения, на- правления которых совпадают с положительными направления- ми координатных осей, считают положительными при условии, если направление растягивающего нормального напряжения по той же координатной площадке сов- падает с положительным на- правлением соответствующей ко- Рис. зл ординатной оси (или если сжи- мающее нормальное напряжение направлено по отрицательному направлению координатной оси).

Если направления нормальных напряжений противоположны указанным, то касательные напряжения следует считать поло­жительными, когда их направления совпадают с отрицательными направлениями соответствующих координатных осей.

Ох	%ху	^хг
%ух	°У	%уг
1	%гу 1	Ог 1
1	1 Si	1 N
О	а	О
<L>	о;	О)
О.	о.	&,
	с(	С(
га	га	га

На рис. 3.1 все напряжения являются положительными. Запишем напряжения в точке по трем координатным площадкам в форме матрицы

направление х\

направление у; | (3.1)

направление г.

В каждой горизонтальной строчке записаны напряжения одного направления в последовательности адресов х, у и г. В каж­дом вертикальном столбике записаны напряжения одного адреса в последовательности направлений х, у, z.

В трех взаимно перпендикулярных площадках можно пред­ставить девять напряжений: три нормальных и шесть касатель­ных. Однако вследствие парности касательных напряжений раз­личные значения могут быть только у шести напряжений: трех нормальных и трех касательных, так как

^ХЧ1 ^{= Х}У" ^Т« ^{= X}zx ^{и %}уг ~ ^%гу (3-2)

(касательные напряжения с индексами из двух одинаковых букв равны между собой независимо от порядка расположения букв в индексе).

Если учесть равенства (3.2), то легко установить, что каса­тельные напряжения, расположенные в матрице симметрично относительно главной диагонали, попарно равны между собой. Учитывая это, матрицу можно переписать сокращенно

(3.1а)

Указания направления и адреса в индексах касательных напряжений можно было бы поменять местами, т. е. первый индекс считать за указание адреса, второй — за указание направ­ления. Все выводимые далее выражения и формулы при такой перестановке индексов останутся без изменения. Такое заклю­чение можно, например, сделать на основании равенств (3.2).