Тема 9. Трёхфазные цепи.

Анализ четырёхпроводной трёхфазной цепи с построением векторной диаграммы. Анализ трёхпроводной трёхфазной цепи с соединением приёмников в звезду с построением векторной диаграммы. Анализ трёхфазной цепи с соединением приёмников в треугольник с построением векторной диаграммы. Мощность трёхфазной цепи.

По 3-х фаз. цепям энергия передается на дальние расстояния и распределяется м/у приемниками.

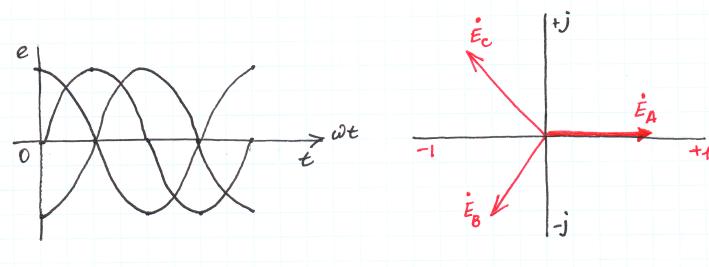
Достоинства: 1. экономия проводник. материалов; 2. Возможность создавать вращ. магн. поле с помощью неподвижн. катушек; 3. Получ. два напряж: фазное и лин.

В 3-х Ф. цепях фействует 3 синусоидальных ЭДС равной амплитуды и частоты, сдвинутые относ. друг друга на 120⁰

3-х Ф. цепь можно получить:

1. Вращением катушек в пост. магн. поле, сдвинутых на 120⁰

2.Вращением магн. поля вокруг 3-х неподвижн. катушек, сдвинутых на 120⁰ (использ на электростанциях в синхронных генераторах);

Отдельная ветвь трехфазной цепи назыв. фазой. Фазы соедин. в звезду (концы фаз – в одну очку, начала – к линиям) и треугольник (конец предыдущей соедин с началом послед. фазы, а места соединений – к линии). Нейтраль – точка соединения концов фаз.

Четырёхпроводная трёхфазная цепь.

Использ. при напряжении до 1000 вольт во внутр. и наружн. проводках стационарных объектов. Фазные и лин. напряж. различны, а токи фаз. и лин. одинаковы. Так как присутствует нейтральн. провод, запишем:

По 2 зак. КИРХ. для контуров, содержащих лин. напряж. можно запис:

(для действ. знач. эти уравн. НЕ выполняются.) При постр. вектр. диаграмм. начинаем с вектр. ЭДС. Чтобы отнять векторы из конца вычитаемого в конец уменьшаемого провести вектор.

Лин. напряж. образ. симметр. систему векторов (U_AB, U_BC,U_CA), т.е. они равны м/у собой по длинне . Лин. напряж. опережает фазное на 30⁰ и больше в раз.

Токи опред по зак. Ома в комплекс. форме:

; (**) . Если нагрузка симметрична, т.е. , то фазные токи образ. симметр. сист. вектров, раны по знач. и величине. и сдвинуты относит соответствующих фазн. ныпряж. на угол: Так как соединение в звезду, то лин. токи равны фаз. Ток в нейтрале опред по 1-му зак. КИРХ. . При симметр. нагрузке . Провод можно убрать.

Если нагрузка несимметр., то токи опред. по уравнению (**),не равны м/у собой, сдвинуты относ. своих напряж. на разные углы. Тогда в нейтральн. проводе появляется ток, но фазные напряж. остаются const благодаря нейтр. проводу. В этом заключается его роль.

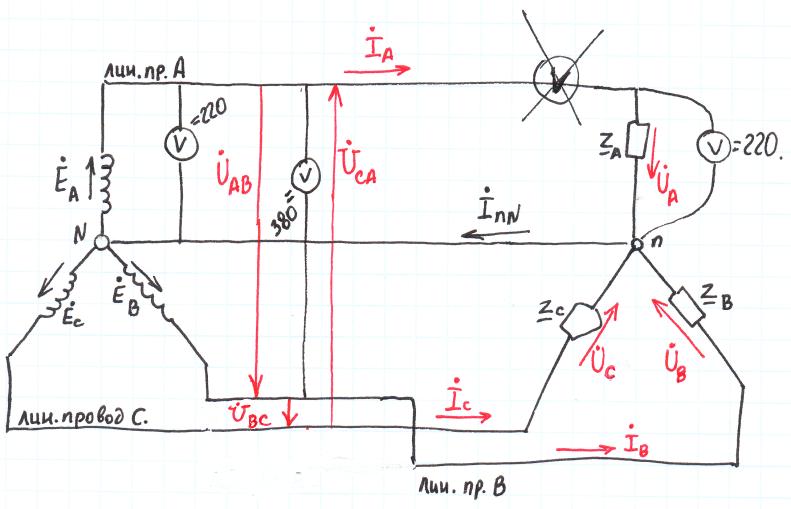
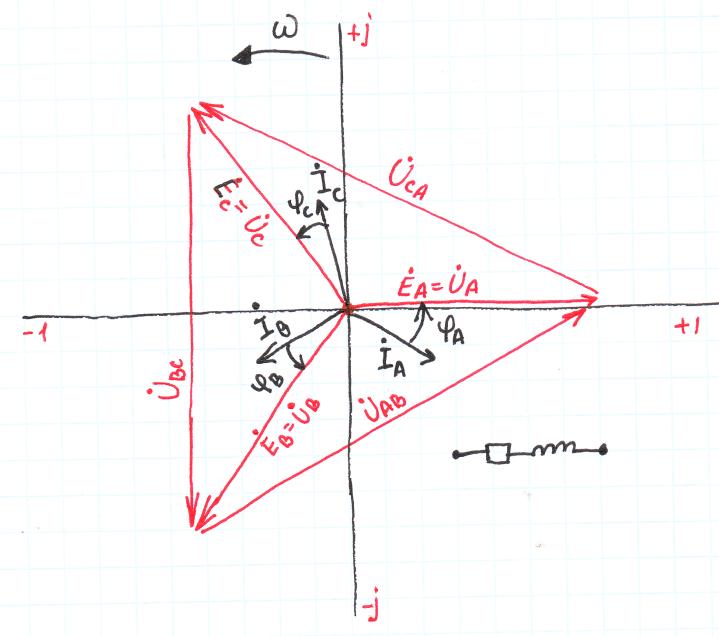
Трёхпроводная трёхфазная цепь с соединением приемников в звезду.

Использ. для передачи энергии на дальние расстояния, электроснабж. предприятий свыше 1000 вольт. Цепи экономичны, но работают только в симметр. режиме. При симетр. режиме , нейтраль не влияет на работу, он не нужен, ветроная диаграмма и расчет будет как и при наличии нейтрального провода – смотри выше.

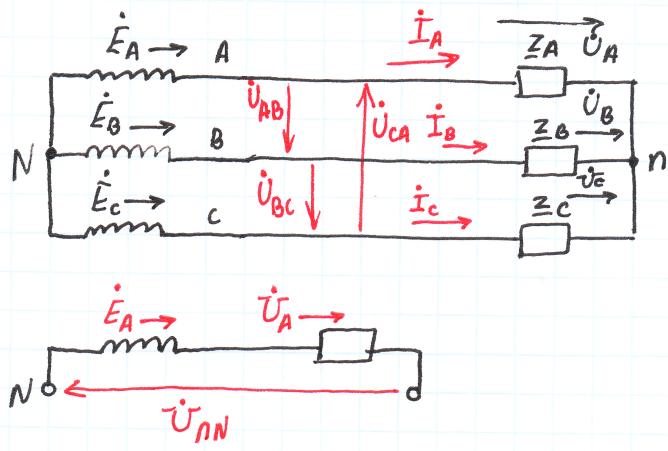
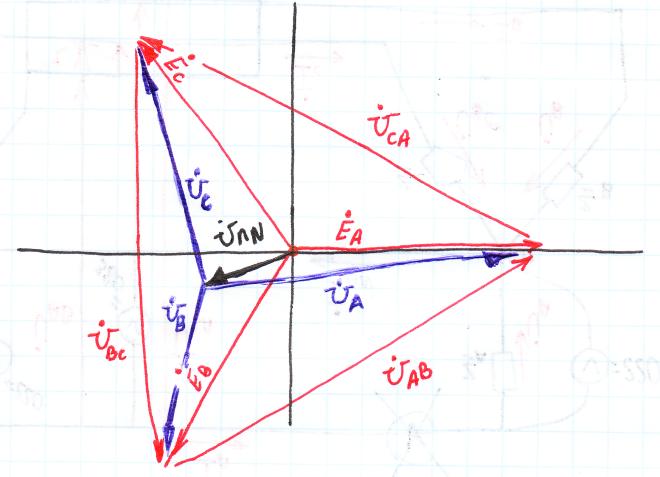
Если нагрузка несимметрична (хотя бы один), то фазн. напряж. и углы сдвига фаз изменяются из-за различного сопротивления фаз. М/у точками N и n появл. напряж. смещения нейтрали U_Nn. Его можно определить:

, где - комплексные проводимости.

К примеру

Вычертим первый контур: ;

Аналогично: ;

Это явление называется перекосом фаз. Фазные напряжения искажаются.

3-хфазная цепь с соединением приемников в треугол.

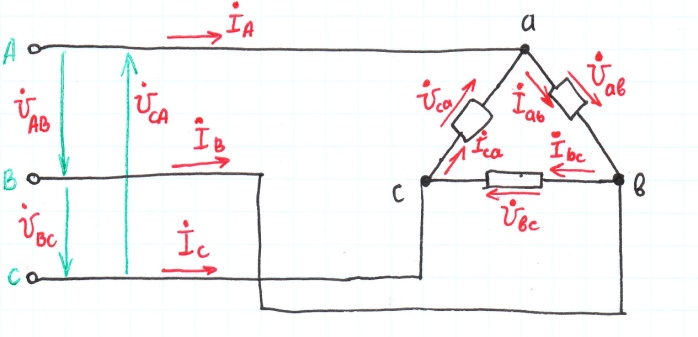
Лин. напряж. образуют симметричную систему ( ). Если сопротивление лин. пр.=0, то фазные напряж. равны линейным. и т.д. – тоже составляют симметричную сист. Т.О. фазные напряжения нагрузки = линейным напряж. Для действ. значений:

Фазные токи опред .по зак. Ома в комплексной форме:

; ;

Линейные токи опред. по 1-му зак. КИРХ. для узлов a,b,c. ; ;

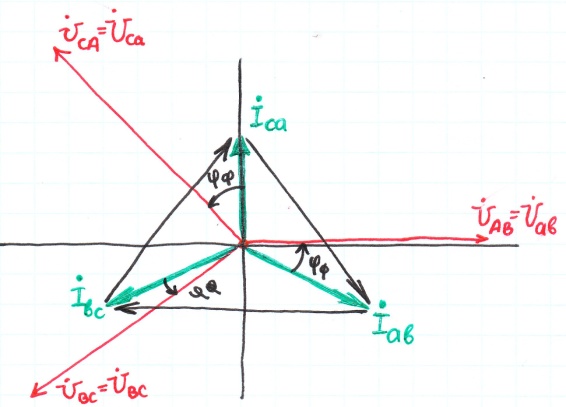
При симметричной нагрузке: Фазные токи равны м/у собой по величине и образ. симметр. систему. Лин. токи тоже равны по величине . Нагрузка акт. индукт.

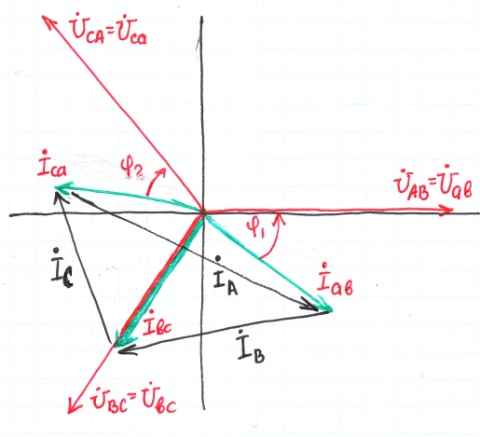
Нагрузка несимметричная: Токи не равны м/у собой. Пусть в фазе ab - активно-индукт., bc – активная, ca – акт-емк.

Мощность трехфазной цепи:

В симметр. системе мощность 3-хФ. цепи равна утроенной мощности одной из фаз. ; - активная мощность

– реактивная.

полная.

В несимметричном – мощн. равна сумме мощностей 3-х фаз. ; ;

Полезная только активная мощность. В промышл. реактивная индукт. мощность достигает больших значений. Для её компенсации ставят конденсаторы или синхронные компенсаторы, кот. вырабат. актив. емкостную мощ. Она идет на компенсацию индукт. мощн. В результате cos повышается, добиваются резонанса токов.

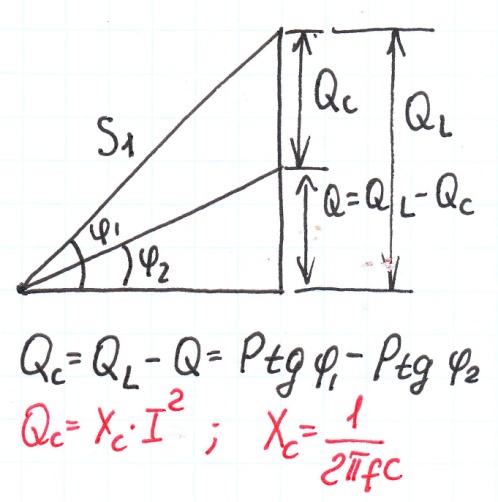
P – акт. мощн, S₁, S₂ – полн. мощность до и после компенсц.

Q_L – реакт. мощн. до компенс, Q_C -реакт. мощность компенс. устройств.