Дисперсия случайной величины

Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.

Если случайная величина  имеет математическое ожидание M , то дисперсией случайной величины  называется величина D = M( - M )².

Легко показать, что D = M( - M )²= M ² - M( )².

Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина M ² >для дискретных и непрерывных случайных величин соответственно вычисляется по формулам

, .

Для определения меры разброса значений случайной величины часто используется среднеквадратичное отклонение , связанное с дисперсией соотношением .

Основные свойства дисперсии:

• дисперсия любой случайной величины неотрицательна, D 0;

• дисперсия константы равна нулю, Dc=0;

• для произвольной константы D(c ) = c²D( );

• дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D(   ) = D( ) + D ( ).

Схема Бернулли - Проводятся опытов, в каждом из которых может произойти определенное событие («успех») с вероятностью (или не произойти — «неудача» — ). Задача — найти вероятность получения успехов в опыте.

Решение:

Количество успехов — величина случайная, которая имеет распределение Бернулли.

Билет 23.

Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения хв, вводят сводную характеристику - выборочную дисперсию.

Выборочной дисперсией D_B называют среднее арифметическое квадратов отклонения наблюдаемых значений

Если все значения x₁, x₂,..., x_n признака выборки объема n различны, то

Если же значения признака x₁, x₂,..., x_k имеют соответственно частоты n₁, n₂,..., n_k , причем n₁+n₂+...+n_k = n, то

Выборочное среднее квадратическое отклонение s – неотрицательный квадратный корень из дисперсии, т.е.

• Несмещённая (исправленная) дисперсия — это случайная величина

.

Для построения оценки нужны критерии, по которым судят о её качестве. Сформулируем некоторые свойства, позволяющие разумным образом выбирать оценки.

1. Оценка  называется несмещенной, если её математическое ожидание равно оцениваемой характеристике случайной величины:

 

,                                                 (1.1)

 

т. е. если она не дает систематической ошибки.

2. Оценка называется состоятельной, если при увеличении числа наблюдений оценка сходится по вероятности к искомой величине, т. е. для любого сколь угодно малого  

 

.                         (1.2)

 

Если известно, что оценка несмещенная, то для проверки состоятельности её удобно пользоваться условием: . Если последнее условие выполнено, то из неравенства Чебышева следует, что оценка состоятельная. .

Иными словами, состоятельность означает, что оценка, построенная по большому числу наблюдений, имеет меньший разброс (дисперсию), т. е. .

Билет 24.

Теорема. Если вероятность наступления события в каждом испытании постоянна и мала, а число независимых испытаний достаточно велико, то вероятность наступления события ровно раз приближенно равна

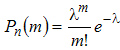,(3.4)

где .

Доказательство. Пусть даны вероятность наступления события в одном испытании и число независимых испытаний . Обозначим . Откуда . Подставим это выражение в формулу Бернулли:

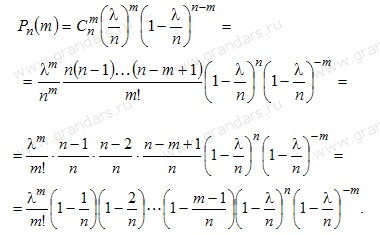
При достаточно большом !!n,, и сравнительно небольшом !!m,, все скобки, за исключением предпоследней, можно принять равными единице, т.е.

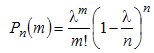
Учитывая то, что достаточно велико, правую часть этого выражения можно рассмотреть при , т.е. найти предел

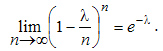
Тогда получим

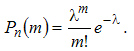(3.5)