|
12.Условия
на границе диэл-ов.
Вблизи
поверхности раздела двух диэлектриков
 должны удовлетв.:
должны удовлетв.:
 и
и
 .
Рассм. границу между диэл-ками с .
Рассм. границу между диэл-ками с
 и
и
 .
В диэл-ах создано поле, напряж-ть кот.
в 1-м диэл-ке = .
В диэл-ах создано поле, напряж-ть кот.
в 1-м диэл-ке =
 ,
а во 2-м - ,
а во 2-м -
 .
Т.к. .
Т.к. ,
то циркуляция ,
то циркуляция
 по выбр. контуру:
по выбр. контуру: ,
откуда ,
откуда
 .
При .
При
 : :
 (1). удовлетворять определенным
граничным условиям, которые вытекают
из соотношений
(1). удовлетворять определенным
граничным условиям, которые вытекают
из соотношений
 и
и
 .Рассмотрим
границу между двумя диэлектриками с
проницаемостями .Рассмотрим
границу между двумя диэлектриками с
проницаемостями
 .
Вследствие того что, .
Вследствие того что,
 циркуляция вектора
циркуляция вектора по
выбранному нами контуру должна быть
равна нулю. При малых размерах контура
и указанном на рис. 2.9 направлении
обхода циркуляция вектора
по
выбранному нами контуру должна быть
равна нулю. При малых размерах контура
и указанном на рис. 2.9 направлении
обхода циркуляция вектора
 может быть представлена в виде
может быть представлена в виде
 ,
откуда при стремящейся к нулю ширине
контура ,
откуда при стремящейся к нулю ширине
контура
 ,
получается равенство. ,
получается равенство.

Векторы
 в двух близких точках, взятых по разные
стороны границы, лежат в одной пл-ти
с нормалью к пов-ти раздела. Представим
каждый из
в двух близких точках, взятых по разные
стороны границы, лежат в одной пл-ти
с нормалью к пов-ти раздела. Представим
каждый из
 в
виде
в
виде
 нормальной и тангенциальной составляющих,
тогда в
соотв-вии с (1) получ, что
нормальной и тангенциальной составляющих,
тогда в
соотв-вии с (1) получ, что
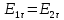 .
Заменив здесь проекции .
Заменив здесь проекции
 на
проекции на
проекции
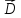 ,
деленные на ,
деленные на
 ,
получ, что ,
получ, что
 .
.
Теперь
возьмем на границе диэл-ов воображаемую
цилиндрич. пов-ть высоты h
(рис. 2.10). Применим к этой пов-ти теор.
Гаусса. Если сторонних зарядов на
границе между диэл-ми
нет,
 Если
устремить высоту цилиндра
h
к
0,
Если
устремить высоту цилиндра
h
к
0, также
будет стремиться к 0. Поэтому в lim
(при проецировании обоих векторов на
одну нормаль) получится
также
будет стремиться к 0. Поэтому в lim
(при проецировании обоих векторов на
одну нормаль) получится
 .
Заменив проекции .
Заменив проекции
 соответствующими
проекциями вектора
соответствующими
проекциями вектора
 ,
умноженными на ,
умноженными на
 ,
получим, что ,
получим, что


|


 должны удовлетв.:
должны удовлетв.:
 и
и
 .
Рассм. границу между диэл-ками с
.
Рассм. границу между диэл-ками с
 и
и
 .
В диэл-ах создано поле, напряж-ть кот.
в 1-м диэл-ке =
.
В диэл-ах создано поле, напряж-ть кот.
в 1-м диэл-ке =
 ,
а во 2-м -
,
а во 2-м -
 .
Т.к.
.
Т.к. ,
то циркуляция
,
то циркуляция
 по выбр. контуру:
по выбр. контуру: ,
откуда
,
откуда
 .
При
.
При
 :
:
 (1). удовлетворять определенным
граничным условиям, которые вытекают
из соотношений
(1). удовлетворять определенным
граничным условиям, которые вытекают
из соотношений
 и
и
 .Рассмотрим
границу между двумя диэлектриками с
проницаемостями
.Рассмотрим
границу между двумя диэлектриками с
проницаемостями
 .
Вследствие того что,
.
Вследствие того что,
 циркуляция вектора
циркуляция вектора по
выбранному нами контуру должна быть
равна нулю. При малых размерах контура
и указанном на рис. 2.9 направлении
обхода циркуляция вектора
по
выбранному нами контуру должна быть
равна нулю. При малых размерах контура
и указанном на рис. 2.9 направлении
обхода циркуляция вектора
 может быть представлена в виде
может быть представлена в виде
 ,
откуда при стремящейся к нулю ширине
контура
,
откуда при стремящейся к нулю ширине
контура
 ,
получается равенство.
,
получается равенство.
 в двух близких точках, взятых по разные
стороны границы, лежат в одной пл-ти
с нормалью к пов-ти раздела. Представим
каждый из
в двух близких точках, взятых по разные
стороны границы, лежат в одной пл-ти
с нормалью к пов-ти раздела. Представим
каждый из
 в
виде
в
виде
 нормальной и тангенциальной составляющих,
тогда в
соотв-вии с (1) получ, что
нормальной и тангенциальной составляющих,
тогда в
соотв-вии с (1) получ, что
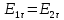 .
Заменив здесь проекции
.
Заменив здесь проекции
 на
проекции
на
проекции
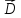 ,
деленные на
,
деленные на
 ,
получ, что
,
получ, что
 .
.
 Если
устремить высоту цилиндра
h
к
0,
Если
устремить высоту цилиндра
h
к
0, также
будет стремиться к 0. Поэтому в lim
(при проецировании обоих векторов на
одну нормаль) получится
также
будет стремиться к 0. Поэтому в lim
(при проецировании обоих векторов на
одну нормаль) получится
 .
Заменив проекции
.
Заменив проекции
 соответствующими
проекциями вектора
соответствующими
проекциями вектора
 ,
умноженными на
,
умноженными на
 ,
получим, что
,
получим, что

