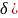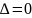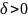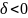- •Операции с матрицами. Единичная матрица. Понятие определителя. Минор элемента, алгебраическое дополнение. Теорема Лапласа. 1.1,1.2
- •Теорема Гамильтона- Кэли. 1.3
- •Запись системы линейных уравнений в общем виде. Матричная запись.
- •Понятие однородной системы. Классификация решений системы. Теорема Крамера. 1.4
- •Запись системы линейных уравнений в общем виде. Матричная запись. Понятие однородной системы. Классификация решений системы. Метод обратной матрицы. 1.4
- •Понятие линейного пространства. Примеры линейных пространств (не менее трех). Понятие подпространства линейного пространства. Примеры (не менее трех). 1.5
- •Доказательство теоремы о базисе линейного пространства. 1.5
- •Исследование векторов линейного пространства Rn на линейную независимость и теорема Кронекера Капелли. Метод Жордана-Гаусса. Ранг матрицы. 1.6
- •Решение некоторых систем линейных уравнений методом Жордана-Гаусса. 1.7
- •Нахождение образа линейного оператора. 1.9
- •Ядро линейного оператора, обозначение, способ нахождения. 1.10
- •Решение однородных систем линейных уравнений в общем случае. 1.11
- •Переход к новому базису. Формулы (1) и (2). 1.12
- •Действия над линейными операторами. 1.13
- •Собственные векторы и собственные значения. Характеристический многочлен. 1.14
- •Линейное пространство геометрических векторов. Орт вектора, проекция вектора. Естественный базис. Направляющие косинусы и их основное свойство (вывод). 2.1
- •Переход к новому базису в пространстве v2. Вывод формул поворота. 2.2
- •Скалярное произведение векторов, следствия (вывод). Выражение скалярного произведения в координатах (вывод). 2.3
- •Определение векторного произведения векторов. Следствия. Выражение векторного произведения в координатах. Условие коллинеарности векторов. 2.4
- •Смешанное произведение векторов. Выражение смешанного произведение в координатах. Нахождение объема тетраэдра. 2.4
- •Вывод уравнения плоскости, проходящей через три заданной точки. 3.2
- •Уравнение прямой в пространстве - общее и каноническое. 3.3
- •Общее уравнение кривой 2-го порядка. Эллипс и его параметры. 3.4
- •Общее уравнение кривой 2-го порядка. Гипербола и ее параметры. 3.4
- •Общее уравнение кривой 2-го порядка. Парабола и ее параметры. 3.4
- •Приведение кривой 2-го порядка к каноническому виду. Решение задач а) и б). 3.5
- •Понятие квадратичной формы. Матрица квадратичной формы. Критерий Сильвестра. Каноническая форма квадратичной формы.
Общее уравнение кривой 2-го порядка. Эллипс и его параметры. 3.4

Ax2+2Bxy+Cy2+2Dx+2Ey+F=0 – общее уравнение кривой второго порядка
Эллипс
это множество точек (x
y),
которые в некоторой специально подобранной
системе координат имеют следующее
каноническое уравнение
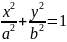
а и в – полуоси эллипса.
Вершины: А1(-а,0) А2(а,0) В1(0,-в) В2 (0,в)
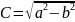 .
Тогда F1(-c.0)
и F2(c.0)
– фокусы эллипса
.
Тогда F1(-c.0)
и F2(c.0)
– фокусы эллипсаF1M и F2M – факальные радиусы
Е=с/а – эксцентриситет. Чем ближе Е к 1, тем более эллипс вытянут вдоль Х
Основное свойство эллипса: Какую бы точку М ни взять на эллипсе, всегда выполняется F1M+F2M=2a
Площадь эллипса равна
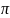 ab
ab
Если а<b то меняем местами оси координат.
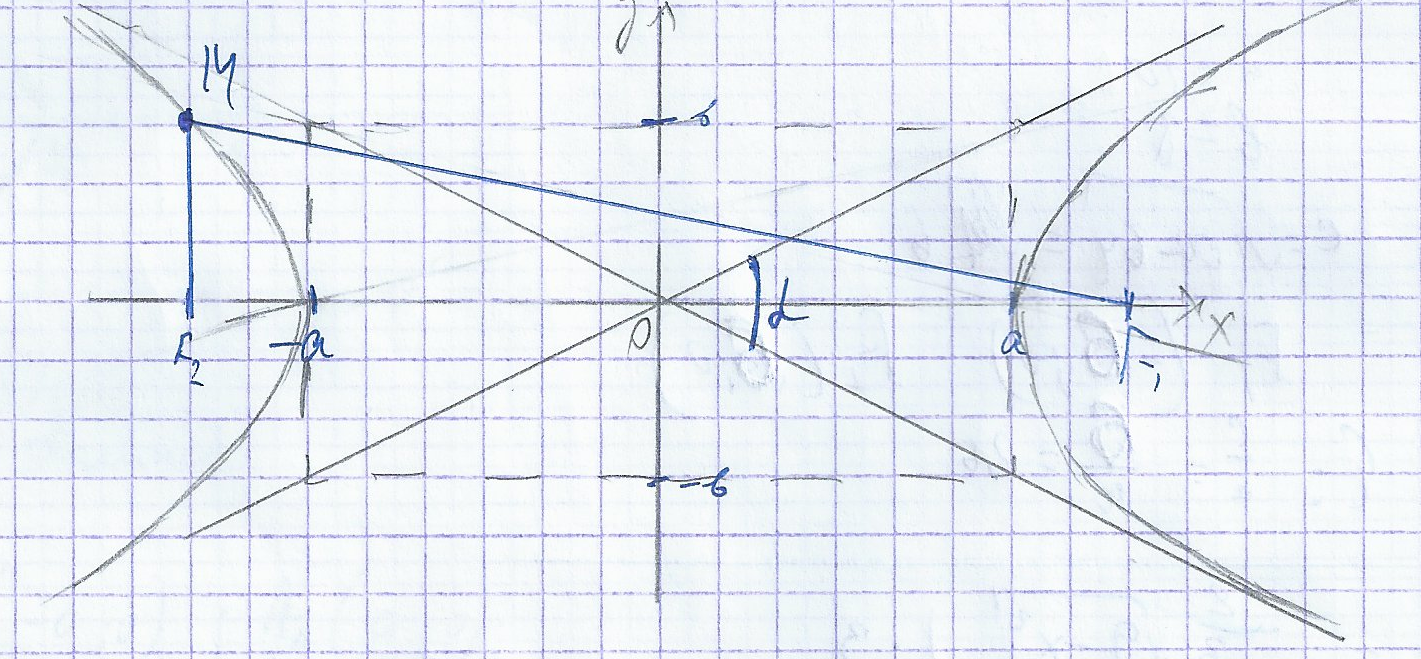
Общее уравнение кривой 2-го порядка. Гипербола и ее параметры. 3.4
Ax2+2Bxy+Cy2+2Dx+2Ey+F=0 – общее уравнение кривой второго порядка
Гипербола-
кривая, в которая в специально подобранной
системе координат имеет уравнение
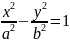
a-действительная полуось, в – мнимая полуось
F1(-c 0) и F2 (с 0) -фокусы
E=c/a – эксцентриситет
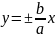 уравнение асимптот
гиперболы
уравнение асимптот
гиперболы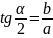

Основное свойство
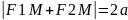
Общее уравнение кривой 2-го порядка. Парабола и ее параметры. 3.4
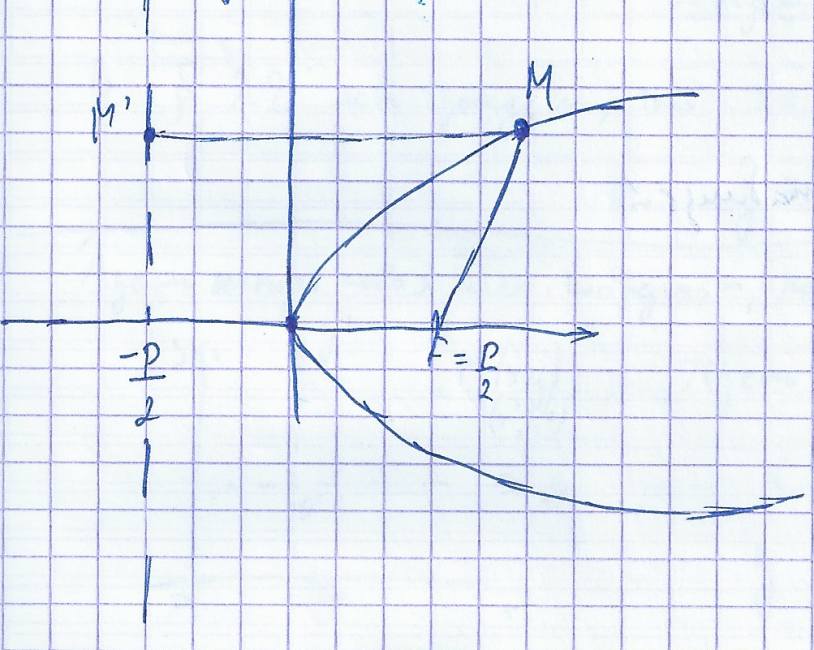
Ax2+2Bxy+Cy2+2Dx+2Ey+F=0 – общее уравнение кривой второго порядка
Парабола – множество точек плоскости, удовлетворяющих уравнению y2=2Px где p>0
Указанная на рисунке прямая – директриса. F-фокус параболы, равен p/2
MM’=MF
Приведение кривой 2-го порядка к каноническому виду. Решение задач а) и б). 3.5
Ax2+2Bxy+Cy2+2Dx+2Ey+F=0 – общее уравнение кривой второго порядка
Поставим следующие задачи:
По уравнению кривой распознать ее тип (эллипс/гипербола/парабола/НЁХ)
Так подобрать новую систему координат (перенести начало, повернуть), чтобы уравнение кривой стало каноническим и можно было ее построить.
Решение задачи А:
Чтоб распознать тип кривой таблицей воспользуйся ты:
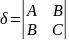
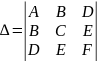
|
|
|
|
Эллипс |
Точка |
|
Гипербола |
Пара пересечения прямых |
|
Парабола |
Пара параллельных прямых или совпадающих прямых или пустое множество |
Решение задачи Б:
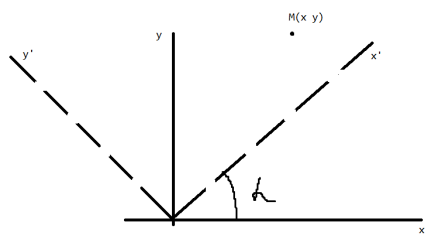
Формулы поворота:
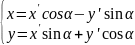
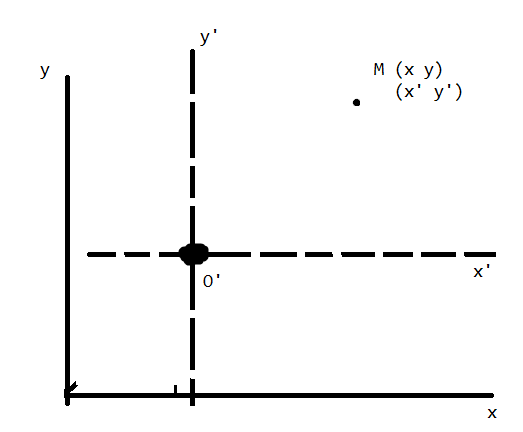
Точка O’ имеет координаты (α,β), тогда
Формулы переноса:
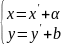
Итак, непосредственно решение:
В=0, то есть отсутствует слагаемое с произведением координат. В этом случае выполняется только параллельный перенос системы координат. Для этого формулы переноса подставляем в исходное уравнение, раскрываем скобки, приводим подобные. После этого числа α и β выбираются так, чтобы уничтожить члены с первыми степенями. После этого строится новая система координат и выполняются конкретные построения.
В исходном уравнении
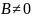 .
В этом случае выполняем поворот системы
координат на угол α
.
В этом случае выполняем поворот системы
координат на угол α
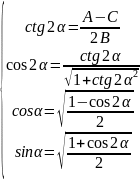
Найденные sin и cos подставить в формулу поворота и далее в формулу переноса исходного уравнения. После раскрытия скобок и приведения подобных выполняем параллельный перенос по правилам пункта 1.