4. Доказательство теоремы о базисе линейного пространства. 1.5

Пусть (е1,у2,…,е_n) – базис линейного пространства. Тогда любой вектор этого пространства разлагается по базису и притом только единственным образом.

Добавим к базису (е1,у2,…,е_n) вектора а. В силу определения базиса полученная система векторов уже линейно зависима. Образуем линейную комбинацию:

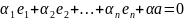Так как эта система линейно зависима, то хотя бы один из коэффициентов НЕ равен нулю. При этом не равен нулю именно .

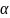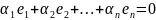Предположим противное ( ), тогда получим , но так как е1, е2, …, е_n образуют базис, то все обязаны равняться нулю. Полученное противоречие доказывает теорему.

4. Исследование векторов линейного пространства Rn на линейную независимость и теорема Кронекера Капелли. Метод Жордана-Гаусса. Ранг матрицы. 1.6

   1. Воспользуемся определением: «Совокупность векторов линейного пространства L называется линейно зависимой, если существуют такие числа Х1, Х2,…,Хn не все равные нулю, что равенство X1*α1+X2*α2+…+Xn*αn=0 Если же равенство выполняется лишь при всех иксах, равных нулю, то система векторов называется линейно независимой»

   2. Распишем это векторное равенство по координатам. Получаем однородную систему с N неизвестными

   3. Образуем матрицу этой системы. Решим, применив преобразование Жордана-Гаусса:

      1. Среди всех элементов 1го столбца выбрать ненулевое (разрешается менять местами строки) Назовем этот элемент разрешающим.

      2. Все элементы разрешающего столбца обнулить, кроме самого разрешающего элемента.

      3. Разрешающую строку и столбец переписать в новую матрицу. Оставшиеся элементы рассчитать по правилу прямоугольника и тоже записать в новую матрицу

      4. В новой матрице отделить разрешающие столбец и строку.

      5. Выделенные строки и столбцы переписать в новую матрицу. К оставшимся применить пункт 2-3

      6. Пройдя все строки, подсчитать r – количество ненулевых строк. Это и будет РАНГОМ матрицы.

      7. Пользуясь теоремой Кронекера-Капелии определить, что:

         1. Если r<n, то система уравнений, по которм построена исходная матрица имеет бесконечное количество решений, в том числе и ненулевых. Векторы будут линейно зависимы.

         2. Если r=n, то система имеет одно решение, но так как нулевое решение есть всегда, оно и будет единственным. Значит система векторов линейно независима.

4. Решение некоторых систем линейных уравнений методом Жордана-Гаусса. 1.7

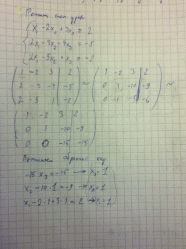
4. Понятие линейного оператора, обозначение, примеры - оператор подобия, оператор проецирования, оператор дифференцирования. Образ оператора и его обозначение. Матрица оператора и ее построение. 1.8

Пусть Xn и Ym– два линейных пространства. Линейным оператором А называется действие, сопоставляющее каждому вектору x из Xn единственный вектор y из Ym. Вектор y называется образом вектора х и обозначается Ах.

Примеры:

• Оператора подобия А:Rn->Rm, сопоставляющий каждому вектору x вектор y=k*x

• Оператор проецирования A:V2->V2, сопоставляющий каждому вектору х его проекцию на ось абсцисс

• Оператор дифференцирования: A:Pn->Pk (Pn- все многочлены степени не ниже n), сопоставляющий каждому многочлену его производную.

Множество векторов {Ax} пространства Ym в которые отображаются всевозможные векторы x из Xn называется образом линейного оператора А (ImgA).

Матрицей линейного оператора А называется матрица А, по столбцам которой находятся координаты образов базисных векторов пространства Xn. Таким образом, если {e1,e2,…en} – базис в Xn, то по столбцам матрицы А должны находиться координаты векторов Ае1, Ау2 и так далее.