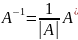Операции с матрицами. Единичная матрица. Понятие определителя. Минор элемента, алгебраическое дополнение. Теорема Лапласа. 1.1,1.2
Матрица – это прямоугольная таблица чисел, заключенная в круглые скобки. Матрица, в которой по главной диагонали стоят единицы, а все остальные элементы – нули называется единичной. Матрицу можно транспонировать – столбец переходит в строку Можно сложить с другой матрицей одного и того же порядка. Можно умножить на число. Тогда каждый элемент будет умножен на это число. Умножение двух матриц: Пусть даны две матрицы А и В, причем колво столбцов А равно числу строк В. Тогда произведением матриц называется новая матрица С, такая что произвольный ее член Cij равен произведению I строки на J столбец.
Пусть А – квадратная матрица порядка N, тогда ее определителем называется число, обозначаемое D(detА), вычисляемое по следующему правилу: ПРАВИЛО ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЯ КРЕСТ-НАКРЕСТ. Определители более высоких порядков чем 2 вычисляются сведением к более низким порядкам. теорема Лапласа: Каждый определитель равен сумме произведений любой строки (столбца) на их алгебраические дополнения. Минором элемента матрицы n-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы А вычеркиванием i-й строки и j-го столбца. Алгебраическим дополнением Аij элемента аij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца (сумма индексов четная - плюс, нечетная - минус)
Понятие определителя матрицы. Теорема Лапласа. Свойства определителя. Вычисление определителя 4-го порядка. Использование EXCEL. 1.2 определитель – см. 1, теор Лапласа см. 1 Свойства определителя:
При транспонировании матрицы ее опред не меняется
Определитель произведения двух матриц равен произведению их определителей
При перестановке двух строк/столбцов определитель меняет знак
Определитель матрицы с двумя одинаковыми строками/столбцами равен нулю
Общий множитель элементов строки/столбца можно вынести за знак определителя
Определитель не изменится, если к любой строке прибавить другую строку, умноженную на некоторое число
При вычислении определителя четвертого порядка надо по теорема Лапласа свести матрицу 4го порядка к произведению четырёх определителей третьего порядка, где либо свести и их ко второму, либо решать как есть.
Определитель в Экселе называется МОПРЕД. Ему в параметры дается адрес крайних (левая верхняя и нижняя правая ячейки) ячеек квадратной матрицы
Понятие обратной матрицы, свойства обратной матрицы. Правило нахождения обратной матрицы. Невырожденная матрица. 1.3 Матрица А-1 назвыается обратной, если А*А-1=А-1*А=Е (единичная матрица)
Свойства обратной матрицы:
(АВ)-1=В-1*А-1
(А-1)Т=(АT)-1
|A-1|= |A|-1
Обратная матрица существует в том и только в том случае, когда она невырожденная (то есть ее определитель не равен нулю)
Чтобы найти обратную матрицу надо:
Вычислить определитель матрицы и убедиться что он не равен нулю
Образовать транспонированную матрицу
Образовать присоединенную матрицу А*, состоящую из алгебраических дополнений элементов транспонированной матрицы
Записать обратную матрицу как
