2.2 Закономерности распределения вероятностей отказов.

Отказы в строительном производстве представляют со­бой случайные величины, которые могут быть дискретными и непрерывными в зависимости от физического смысла иссле­дуемого явления, и характеризуются функциями распределе­ния вероятностей.

Если - случайная величина, то вероятность того, что она примет значение, меньшее некоторого числа х

,

называется интегральной функцией распределения веро­ятностей или законом распределения вероятностей случайной величины отказов.

Для случайных дискретных величин F(x) есть неубывающая ступенчатая функция; для непрерывных случайных величин F(x) непре­рывная функция для всех значений х.

Производная от f(x)=F(x) , если она существует, называ­ется плотностью (или функцией) распределения вероятностей отказов.

Изучение теоретических законов распределения случайных величин и сфер их пригодности для различных строительных процессов и методов организации строительно­го производства весьма важно, так как позволяет резко сокра­тить объем статистического материала и продолжительность наблюдений для описания поведения числа и величины отка­зов.

Равномерное распределение справедливо для тех случа­ев, когда случайное событие лежит в определенном времен­ном интервале, причем появление его в любой момент време­ни равновероятно.

Пусть благоприятное событие распределено равномерно на временном интервале Т и плотность распределения постоянна f(x)=const на всем участке действия закона от до . Вероятность события равна 1. Отсюда плотность распределения:

Интегральная функция распределения:

Математическое ожидание случайной величины, имеющее равномерное распределение:

Дисперсия распределения:

, т.е. дисперсия равномерного распределения растет пропорционально квадрату интервала, на котором возможно появление отказов процесса.

Показательное распределение является одним из наибо­лее распространенных в строительном производстве благодаря своей простоте и приблизительному соответствию распределению отказов сложных многоэлементных систем. Накоп­ление сведений о проведении разнообразных взаимосвязан­ных строительных процессов деятельности строительно-производственных подразделений приводит к другим законам, более точно отражающим реальное распределение, но одновременно во много раз усложняющим вычисления.

Функция распределения показательного закона записывается следующим образом:

F(x) =

Закон справедлив для Х > 0 и зависит только от одном параметра , характеризующего интенсивность (опасность) отказов.

Плотность распределения при показательном распределении:

f(x) = dF(x)/d(x} = ,

т. е. представляет собой монотонно убывающую функцию.

Математическое ожидание:

Дисперсия показательного распределения:

Т.е. - это свойство показательного распределения можно использовать при оценке возможности его применения для описания экспериментальных данных.

Распределением Вейбулла нередко пользуются при опре­делении надежности ряда процессов. Функция записывается в следующем виде:

Это равенство справедливо для х>0, но зависит от двух параметров и . При распределение Вейбулла переходит в показательное.

Рис. 2.1 Законы распределения вероятностей Вейбулла (а), Гаусса (б)

Рис. 2.2. Закон распределения вероятностей Пуассона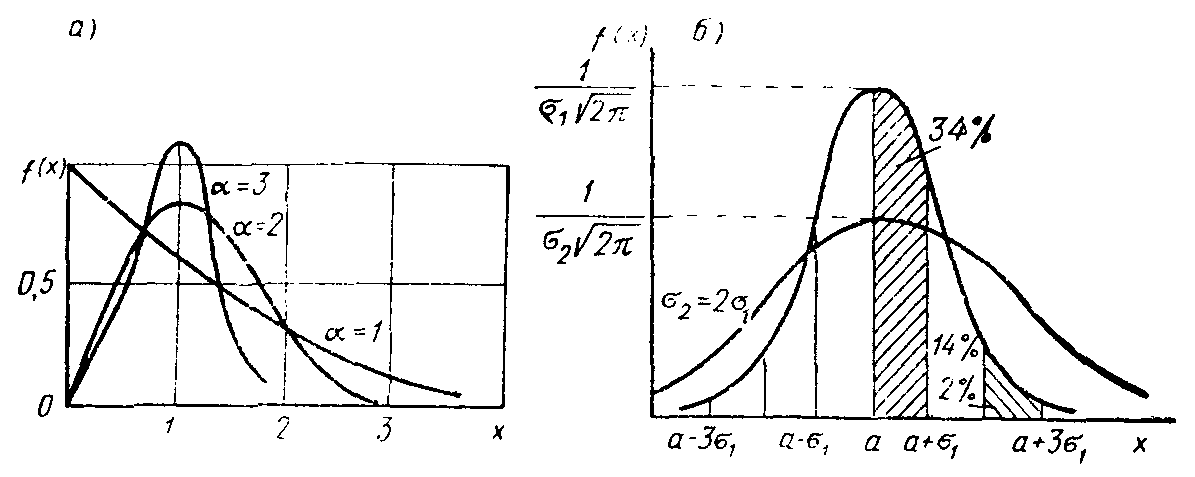

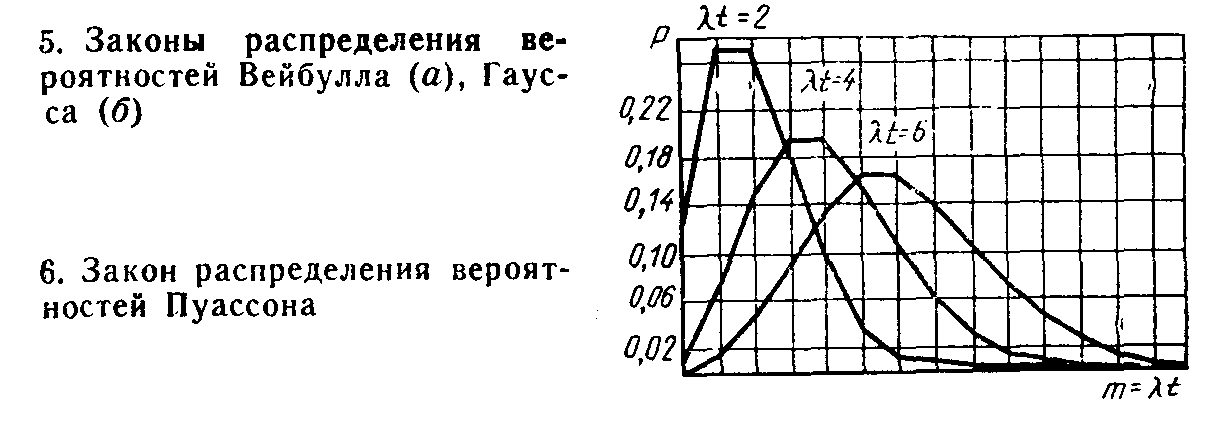рис.2.1 рис. 2.2

Нормальное распределение широко применяют в теории надежности для описания событий, зависящих от многих фак­торов, каждый из которых слабо влияет на распределение случайного события. По нормальному закону распределяются параметры выработки исполнителей и бригад на строительных процессах, продолжительности технологических стадий и строительства типовых объектов и др.

Плотность распределения нормального закона записыва­ется в следующем виде:

,

где - математическое ожидание;

- дисперсия распределения.

Чем больше дисперсия, тем более плоской получается кривая распределения.

Вероятность попадания случайной величины, распределенной по нормальному закону, на заданный интервал измерения параметра х от до обычно определяется интегрированием плотности распределения.

Распределение Пуассона наиболее успешно использует­ся для определения вероятности дискретных событий или по­явления потока событий. Если независимые события следуют с конкретной средней частотой, то расчет вероятности Р_т , т.е. вероятности того, что за какой-то отрезок времени t произойдет ровно т событий, производится по закону Пуассона.

Закон Пуассона записывается в следующем виде:

Распределение Пуассона имеет следующее свойство: математическое ожидание и его дисперсия равны одной и той же величине .

Биноминальным называется такое распределение, при котором его члены получаются в результате разложения би­нома (р + q)ⁿ, где р и q - вероятности появления и непоявле­ния события в каждом из п опытов. Очевидно, что сумма всех членов указанного разложения тождественно равна 1, по­скольку (р + q)ⁿ=1 ⁿ, а каждый член разложения представляет собой определенную вероятность, рассчитанную по формуле:

,

где - число сочетаний из n по m; q=1-p.

В курсовой работе для описания возможных отказов для комплекса работ по балластировки участка пути рекомендовала бы нормальное распределение. Т.к. при производстве работ на данную систему влияет большое количество случайных факторов. Для описания возможных отказов работ на станции рекомендовала бы биноминальное распределение, т.к. строительство ведется все время на различных участках станции, несколькими этапами строительства, т.е. присутствует большая вероятность различного сочетания вероятностей появления и непоявления событий.

Важно отметить, что на эффективность организационно-технологической надежности влияет объединение в производственном процессе технических и социологических систем, а также их воздействие с внешней средой.