19. Резонансные явления в цепях синусоидального тока

Резонанс — особый режим работы электрической цепи, содержащей участок с разнородными реактивными элементами (L и C), при котором эквивалентное реактивное сопротивление или реактивная проводимость этого участка равны нулю. По отношению к внешней части цепи этот участок в резонансном режиме ведет себя как чисто активное сопротивление, поэтому на входе такого участка цепи (иначе его называют колебательным контуром) ток и напряжение совпадают по фазе. Резонансный режим является частным случаем рассмотренных выше режимов работы цепи синусоидального тока (см.табл.3.5), при котором индуктивное сопротивление (проводимость) цепи компенсируется емкостным сопротивлением (проводимостью): , .

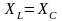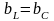Резонансная частота — это частота входного сигнала, при которой в цепи наблюдается резонанс напряжений или токов. В сложной разветвленной цепи с большим количеством разнородных реактивных элементов резонансных частот может быть несколько. Их количество определяется параметрами элементов цепи и их соединением.

Резонанс напряжений. Резонанс напряжений наблюдается в цепи с последовательно соединенными разнородными реактивными элементами (рис.3.7, табл.3.5). Иначе такую цепь называют последовательным колебательным контуром. Ранее для последовательного RLC-контура было определено его эквивалентное комплексное сопротивлени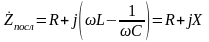е: , где .

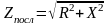Условием резонанса в этом случае будет равенство нулю реактивного сопротивления цепи (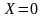 ), ведь только при этом условии цепь будет проявлять чисто активные свойства, т.е. 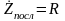. Таким образом, для последовательного RLC-контура получим: , ,

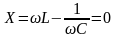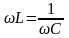откуда определяется то единственное значение частоты входного сигнала 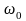, при котором в цепи будет наблюдаться резонанс напряжений (рис.3.15): , .

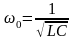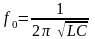При резонансе напряжения на индуктивном и емкостном элементах 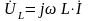и 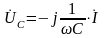равны по значению (рис.3.16), но противоположны по фазе, поэтому они компенсируют друг друга. Следовательно, общее падение напряжения на рассматриваемом участке цепи при резонансе будет равно только падению напряжения на резистивном элементе: .

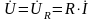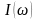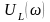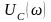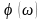Зависимости , , называются резонансными кривыми. Зависимость называется фазочастотной характеристикой (ФЧХ). На рис.3.16 эти характеристики приведены для колебательных контуров с различным по величине активным сопротивлением R. Оно и определяет максимальные значения тока и напряжений при резонансе (на рис.3.16 сплошной линией показаны кривые для меньшего значения R, точками — для значительно большего R).

Практическое значение явления резонанса в цепях синусоидального тока. В резонансном режиме напряжения либо токи на отдельных элементах цепи могут в несколько раз превысить значение соответствующих входных величин, что в промышленных условиях может привести к аварии. Однако явление резонанса имеет и позитивную сторону — оно дает возможность выделить полезный сигнал на резонансной частоте, что широко используется в теле- и радиоприемных устройствах.

20. Условия резонанса в цепях переменного тока ( НУЖНО ДОБАВИТЬ!!)

В цепи переменного тока, в которой индуктивность и  емкость соединены параллельно, может возникнуть резонанс токов при условии равенства токов в индуктивности L и емкости C

Резонанс в электрической цепи можно получить тремя способами: изменяя угловую частоту ? источника переменного тока, индуктивность L или емкость С. Различают резонанс при последовательном соединении L и С — резонанс напряжений и при параллельном их соединении — резонанс токов. Угловая частота ?₀, при которой наступает резонанс, называется резонансной, или собственной частотой колебаний резонансного контура.