6. Анализ линейного электрической цепи методом законов Кирхгофа

7. Метод узловых напряжений

Метод узловых напряжений состоит в определении  напряжений  между узлами сложной электрической цепи путем решения уравнений, составленных по первому закону Кирхгофа, куда в качестве неизвестных входят напряжения между узлами цепи. Этот метод позволяет уменьшить количество уравнений системы до величины: (k-1), где k - количество узлов сложной электрической цепи. Данный метод целесообразно использовать, когда l>2(k - 1), где l - количество ветвей сложной электрической цепи.

Узловыми напряжениями называют напряжения между каждым из (k-1) узлов и одним произвольно выбранным опорным узлом. Потенциал опорного узла принимается равным нулю. На схеме такой узел обычно отображают как заземленный.

Сущность метода заключается в том, что вначале решением системы уравнений определяют потенциалы всех узлов схемы по отношению к опорному узлу. Далее находят токи всех ветвей схемы с помощью закона Ома по формуле 

8. Метод контурных токов

Метод контурных токов (МКТ) основан на составлении уравнений по второму закону Кирхгофа для независимых контуров цепи. При этом предполагается, что в каждом условно изолированном контуре цепи протекает свой контурный ток (чисто расчетная, абстрактная величина). В методе используется следующее свойство: ток в любой ветви может быть представлен в виде алгебраической суммы «контурных» токов, протекающих по этой ветви.

Основная цель применения данного метода — уменьшение количества расчетных уравнений путем уменьшения числа неизвестных (вместо большого числа реальных токов в ветвях определяются промежуточные величины — контурные токи).

Метод контурных токов предполагает:

1. Выбор направления токов в ветвях схемы и направления контурных токов в контурах схемы. Обычно контуры выбирают по «ячейкам» схемы. Если в схеме есть источники тока, то контур выбирают так, чтобы он проходил через ветвь с источником тока, в этом случае контурный ток считается известным (равным току источника). После этого ветвь с данным источником тока уже не должна входить в следующий выбранный контур.

2. Составление системы уравнений по МКТ. Система уравнений по МКТ для n контуров имеет следующую каноническую форму записи:

,

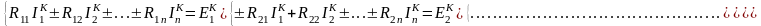где 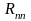— собственное сопротивление п-го контура (сумма сопротивлений ветвей, входящих в контур п) . Собственные сопротивления — это коэффициенты, располагающиеся по главной диагонали матрицы сопротивлений, они всегда положительны;

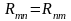— сопротивление ветви, общей для контуров п и т (взаимное сопротивление). Если контурные токи в общей ветви сонаправлены, то взаимное сопротивление положительно, в противном случае — отрицательно. Коэффициенты вида располагаются зеркально относительно главной диагонали матрицы сопротивлений;

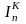— контурный ток п-го контура;

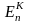— контурная ЭДС (алгебраическая сумма ЭДС, действующих в контуре п) ;

Если в цепи есть контуры с источниками тока, то контурные токи этих контуров считаются известными, а уравнение по второму закону Кирхгофа для данного контура не составляется (вместо него в систему уравнений добавляется уравнение вида 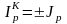). Это условие обосновано, поскольку составление уравнения по второму закону Кирхгофа для контура, включающего ветвь с источником тока, лишено физического смысла, т.к. собственное сопротивление такого контура бесконечно велико (уравнение несбалансировано). Решением приведенной системы уравнений являются значения контурных токов, которые представляют собой промежуточные величины.