Вопрос 16

Свойства функций, непрерывных на отрезке: ограниченность, достижимость точных граней.

Опр: f(x) наз. Непрерывной на [a,b]если она непрерывна в каждой точке интервала (a,b), в т.а непрерывна слева, а в b-справа.

Теорема (вейерштрасс) Если f(x) непрерывна на [a,b], то она ограниченна на этом отрезке (обратное неверно)

Доказательство:

Предположим, что   непрерывна, но неограниченна:    .

По лемме Больцано-Вейерштрасса, из последовательности  можно извлечь частичную последовательность  , сходящуюся к пределу  :

. По теореме о предельном переходе в неравенстве  . Так как 

,  . Мы пришли к противоречию.

То есть   - ограничена. 

Теорема

Если f(x) непрерывна на [a,b], то она достигает на нем своей точной верхней и нижней грани.

Доказательство.

Докажем, что достигается sup (inf - аналогично). Предположим, что   на отрезке  . Рассмотрим вспомогательную функцию  , которая непрерывна (знаменатель  ) и ограничена на   :  .  ,  . Таким образом  . Но M - наименьшая из верхних граней, а мы пришли к противоречию, т. к.   - тоже верхняя грань. Теорема доказана.

Теорема:(больцано-коши)

Если f(x) непрерывна на [a,b] и принимает на его концах значения разных знаков, то на [a,b] имеется хотя бы один 0 для f(x).

Доказательство:

Рассмотрим функцию   Она непрерывна на отрезке   и  ,   Покажем, что существует такая точка  , что   Разделим отрезок   точкой   на два равных по длине отрезка, тогда либо   и нужная точка   найдена, либо   и тогда на концах одного из полученных промежутков функция   принимает значения разных знаков (на левом конце меньше нуля, на правом больше).

Обозначив полученный отрезок  , разделим его снова на два равных по длине отрезка и т.д. Тогда, либо через конечное число шагов придем к искомой точке  , либо получим последовательность вложенных отрезков   по длине стремящихся к нулю и таких, что

Пусть   - общая точка всех отрезков  ,   Тогда   и в силу непрерывности функции 

Поскольку

получим, что 

Теорема

Если f(x) ∈ C([a,b]) и f(a)<>f(b) то ∀c, заключенного между a и b ∃ ξ ∈[a,b]. f(ξ)=c

Доказательство

Пусть A:=f(a) B:=f(b), A<B-----Если c=A, то ξ=а, т.к. f(ξ)=c----Если с=B, то ξ=b, т.к. f(ξ)=c----Пусть A<C<B----U(x)=f(x)-c

U(a)=f(a)-c=A-c<0----U(b)=f(b)-c=B-c>0 ----U(x) ∈C([a,b])

Т.о. ф-я U удовлетворяет всем условиям 1-ой т.Больцано-Коши и ∃ ξ ∈ [a,b]: U(ξ)=0f(ξ)-c=0f(ξ)=c.

Следствие: если f(x) непрерывна на [a,b] и m=inf f(x),x∈[a,b], M=sup f(x),x∈[a,b], то мн-во значений принимаемых функцией на [a,b]=[m,M]

Теорема

Если f(x) ∈ C([a,b]) и f(x) возрастает на [a,b], то на отрезке [f(a),f(b)] определена ф-я x=g(y), обратная к f(x), непрерывная и строго монотонно возрастающая.

Доказательство

По условию функция f строго возрастает на множестве X. Это значит для любыхx1,x2∈Xи x1<x2 следует f(x1)<f(x2). Отсюда следует, что функция f обратима на X, следовательно, для нее существует обратная функция f−1:Y→X. Покажем, что функция f−1 строго возрастает на множестве Y. Пусть y1 и y2- любые точки из Y и y1<y2. Докажем, что x1=f−1(y1)<x2=f−1(y2). Допустим, чтоx1≥x2. По условию функция f строго возрастает на X, поэтому из условия x1≥x2вытекает неравенствоy1=f(x1)≥y2=f(x2), что противоречит условию y1<y2. Т.о., условие строгой монотонности функции является достаточным для существования обратной функции.

Билет 17

Теорема об обратной функции.

Пусть функция f(x) определена, непрерывна и строго монотонно возрастает (убывает) на отрезке [a,b]. Тогда на отрезке [f(a),f(b)] определена обратная функция f(-1)(x), которая также непрерывна и строго монотонно возрастает (убывает).

Билет 18

Билет 19

     Вычисление пределов

1. Случай, когда при х стремящемся к  а функция f ( x ) представляет отношение двух бесконечно малых величин

а) Сначала нужно убедится, что предел функции нельзя найти непосредственной подстановкой и при указанном изменении аргумента она представляет отношение двух бесконечно малых величин. Делаются преобразования, чтобы сократить дробь на множитель, стремящийся к 0. Согласно определению предела функции аргумент х стремится к своему предельному значению, никогда с ним не совпадая.

Вообще если ищется предел функции при х стремящемся к а , то необходимо помнить, что х не принимает значения а, т.е. х не равен а.

б) Применяется теорема Безу. Если ищется предел дроби, числитель и знаменатель которой многочлены, обращающиеся в 0 в предельной точке х=а, то согласно вышеназванной теореме оба многочлена делятся без остатка на х-а.

в) Уничтожается иррациональность в числителе или в знаменателе путем умножения числителя или знаменателя на сопряженное к иррациональному выражение, затем после упрощения дробь сокращается.

г) Используется 1-й замечательный предел (4.1).

д) Используется теорема об эквивалентности бесконечно малых и следующие б.м.

2. Случай, когда при х стремящемся к  а функция f ( x ) представляет отношение двух бесконечно больших величин

а) Деление числителя и знаменателя дроби на наивысшую степень неизвестного.

б) В общем случае можно использовать правило

3. Случай, когда  при х стремящемся к а функция f ( x ) представляет произведение бесконечно малой величины на бесконечно большую

Дробь преобразовывается к виду, числитель и знаменатель которой одновременно стремятся к 0 или к бесконечности , т.е. случай 3 сводится к случаю 1 или случаю 2.

4. Случай, когда  при х стремящемся к  а функция f ( x ) представляет разность двух положительных бесконечно больших величин

Этот случай сводится к виду 1 или 2 одним из следующих способов:

а) приведение дробей к общему знаменателю;

б) преобразование функции к виду дроби;

в) избавление от иррациональности.

5. Случай, когда при  х стремящемся к  а функция f ( x ) представляет степень, основание которой стремится к 1, а показатель к бесконечности .

Функция преобразовывается таким образом, чтобы использовать 2-й замечательный предел (4.2).

    Теорема  (о замене переменных в пределе)

Пусть:

1)      функция   переменной х преобразуется с помощью подстановки   в функцию   переменной z получается 

2)        (конечный предел) причем вблизи точки   

3)        тогда 

 

            Доказательство по Гейне.

Рассмотрим произвольную последовательность  .

Положим  , тогда по Гейне последовательность   сходится к  , причем   следовательно снова по Гейне с учетом  , имеем что последовательно   сходится к А, т.е. 

 

Примечание

В доказанной теореме функция   представлена как сложная функция переменной х посредством промежуточной переменой     поэтому доказанную теорему можно понимать как теорему о пределе сложной функции.

Эталонные пределы

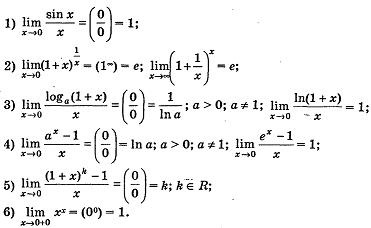
Второй замечательный предел e = lim_x (1+1/x)^x

Сравнение функций.О-символика.

Определение 15 (символ О). Если для функций f(x), g(x) существуют постоянные c>0, >0, такие, что |f(x)| c |g(x)| при |x-a|<, x a, то говорят, что f является ограниченной по сравнению с функцией g в окрестности точки a и пишут, что f(x) = O(g(x)) при x a.

Определение 16 (функции одного порядка). Если f=O(g) и g=O(f) при x a  f и g — одного порядка при x a.

Определение 18 (символ о). Говорят, что функция f является бесконечно малой по сравнению с g при x a, и пишут f=o(g), x a, если выполнено соотношение f(x) = (x)g(x), где lim_x a (x) = 0. Иначе говоря lim_x a f(x)/g(x) = lim_x a (x) = 0.

Определение 19. Если f=o(g) при x a и g(x) - бесконечно малая при x a, то говорят, что f(x) - бесконечно малая более высокого по сравнению с g(x) порядка при x a.

Определение 20. Если f(x), g(x) -бесконечно большие при x a и f=o(g) при x a, то говорят, что g - бесконечно большая более высокого порядка по сравнению с f .