Билет №8
Свойства сходящихся последовательностей, связанные с неравенствами.
Теорема 3. Если последовательности {xn}, {yn}, {zn} таковы, что
То последовательность {yn} сходится и
Доказательство:
►
По определению предела для любого ε>0 найдутся номера N1 = N1(ε) и N2 = N2(ε), такие, что xn∈Uε(a) при всех n≥N1 и zn∈Uε(a) при всех n≥N2. Отсюда и из условия (8) следует (см. рис.),
что при всех n≥N,
где N
= max(N0,N1,N2),
выполняется условие yn∈Uε(a).
Это означает, что существует
.◄
Замечание 4. Теорему 3 называют теоремой о трех последовательностях или теоремой о пределе "зажатой" последовательности.
Теорема 4. Если
Причем a<b(16), то
Доказательство:
►
Как и в теореме 1, выберем ε > 0 таким, чтобы ε -окрестности точек a и b (см.рис) не пересекались (возьмем, например, ε = (b - a)/3 > 0).
Согласно определению предела по заданному ε можно найти номера N1 и N2 такие, что xn∈Uε(a) при всех n≥N1 и yn∈Uε(a) при всех n≥N2. Пусть N0= max(N1,N2). Тогда при всех n≥N0 выполняются неравенства:
Xn<a+ ε <b- ε < yn,
Откуда следует утверждение (17). ◄
Следствие 1.
Если
то
Доказательство:
►
Для доказательства утверждения (18) достаточно в теореме 2 взять yn = b, n∈N. ◄
Следствие 2.
Если
и
То a≥b (20)
Доказательство:
►
Предположим, что неравенство (20) не выполняется. Тогда a < b и по теореме 4 справедливо утверждение (17), которое противоречит условию (19). Поэтому должно выполняться неравенство (20). ◄
Замечание 5.
В частности, если для сходящейся
последовательности {xn}
выполняется для
всех n∈N
(или для всех n≥N0)
неравенство xn≥a
(xn≤b),
то
.
Отсюда следует, что если все члены
сходящейся последовательности {xn}
принадлежат отрезку [a,b],
т. е. a≤xn≤b
для всех n∈N,
то и предел этой последовательности
принадлежит отрезку [a,
b],
т. е.
Замечание 6.
В следствии 2 утверждается, что если
соответствующие члены двух сходящихся
последовательностей связаны знаком
нестрогого неравенства, то такое же
неравенство справедливо и для пределов
этих последовательностей. Короче:
предельный переход сохраняет знак
нестрогого неравенства. Однако знак
строгого неравенства, вообще говоря,
не сохраняется, т. е. если xn>yn
при n≥N0
и последовательности {xn},
{yn}
сходятся то
Арифметические операции над сходящимися последовательностями.
Доказательство:
►
Билет №9 Предел монотонной последовательности.
Последовательность {xn} называют возрастающей (неубывающей), если для любого n∈N выполняется неравенство:
xn+1≥xn (1)
Аналогично последовательность {xn} называют убывающей (невозрастающей), если для любого n∈N справедливо неравенство
xn+1≤xn (2)
Если неравенство (1) можно записать в виде xn+1>xn, а неравенство (2) — в виде xn+1<xn, то последовательность {xn} называют соответственно строго возрастающей и строго убывающей. Возрастающую или убывающую последовательность называют монотонной, а строго возрастающую или строго убывающую — строго монотонной.
Если неравенство (1) выполняется при n≥n0, то последовательность {xn} называют возрастающей, начиная с номера n0 (при n≥n0). Аналогично вводятся понятия убывающей, строго убывающей и строго возрастающей последовательности, начиная с номера n0 (при n≥n0).
Признак Вейерштрасса сходимости монотонной последовательности.
Теорема(о существовании предела монотонной последовательности)
1)Если последовательность {xn} монотонно возрастает (убывает) и ограничена сверху (снизу), то у нее существует конечный предел, равный sup{xn} (inf{xn}).
2)Если последовательность {xn} монотонно возрастает (убывает), но сверху (снизу) не ограничена, то у нее существует предел, равный +∞ (-∞).
►Ограничимся доказательством теоремы для случая ограниченной сверху и возрастающей последовательности. Если последовательность {xn} ограничена сверху, т. е. множество чисел x1,x2,…,xn,… ограничено сверху, то по теореме о существовании верхней грани существует точная верхняя грань этой последовательности, определяемая условиями (7), (8). Так как {xn} — возрастающая последовательность, то
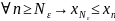(9)
Из (7)-(9) следует, что
Это означает, согласно определению предела, что
◄
Замечание 1. Теорема 1 остается справедливой для последовательности, ограниченной сверху (снизу) и возрастающей (убывающей), начиная с некоторого номера.
Число е.
Рассмотрим последовательность {xn}, где
и покажем, что эта последовательность
возрастающая и ограниченная сверху.
Используя формулу бинома Ньютона,
получаем
Запишем xn в следующем виде:
Все слагаемые в суммах (16) и (17) положительны,
причем каждое слагаемое суммы (16) меньше
соответствующего слагаемого суммы
(17), так как,
а число слагаемых в сумме (17) на одно
больше, чем в сумме (16). Поэтому xn<xn+1
для
всех n∈N,
т. е. {xn}
— строго возрастающая последовательность.
Кроме того, учитывая, что
,
из равенства (16) получаем
.
Так как
при k∈N,
то, используя формулу для суммы
геометрической прогрессии, получаем:
.
Следовательно,
т.е. {xn} – ограниченная последовательность. По теореме 1 существует предел. Этот предел обозначается буквой e. Таким образом,
Число е является иррациональным, оно служит основанием натуральных логарифмов и играет важную роль в математике. Справедливо приближенное равенство
е ≈ 2,718281828459045.