Билет №4

1. Верхняя и нижняя грани числовых множеств. Множество X вещественных чисел (X С R) называется ограниченным сверху, если существует вещественное число С такое, что все элементы множества X не превосходят С, т. е.

1. 

Всякое вещественное число С, обладающее свойством (1), называют верхней гранью числового множества X. Аналогично множество X С R называется ограниченным снизу, если

2. 

Всякое число С', удовлетворяющее условию (2), называют нижней гранью числового множества X. Если числовое множество ограничено как сверху, так и снизу, его называют ограниченным, т. е. {X — ограниченное множество} <=>

2. Определение точной верхней и нижней грани. Пусть числовое множество X ограничено сверху тогда выполняется условие (1), а число С является верхней гранью множества X. Ясно, что любое число, большее С, также является верхней гранью множества X. Таким образом, ограниченное сверху числовое множество имеет бесконечно много верхних граней, среди которых особую роль играет наименьшая. Речь идет о числе М, обладающем следующими свойствами:

а) М — верхняя грань множества X;

б) Любое число М' меньшее М, не является верхней гранью множества X.

Это число М является точной верхней гранью множества X.

Определение 1. Число М называется точной верхней гранью числового множества X, если выполняются следующие условия:

Точная верхняя грань числового множества X обозначается supX (читается "супремум"). Таким образом,

Замечание 1. Число М = supX может как принадлежать, так и не принадлежать множеству X. Например, если X — множество чисел ж таких, что 1 <= х < 2, то supX = 2. 2 не пренадлежит множеству X.

Замечание 2. Из определения точной верхней грани следует, что если у числового множества X существует точная верхняя грань М, то она единственна.

Определение 2. Число m называется точной нижней гранью числового множества X, если выполняются следующие условия:

Точная нижняя грань множества X обозначается inf X (читается "инфимум"). Таким образом,

3. Существование точной верхней (нижней) грани.

Теорема 1. Если непустое множество вещественных чисел X ограничено сверху, то существует supX; если непустое множество X ограничено снизу, то существует inf X.

Билет №5 Билет №6 Билет№7

Определение предела последовательности.

Определение 1. Число a называется пределом последовательности {xn}, если для каждого ε>0 существует такой номер N_ε что для всех n∈N выполняется неравенство:

Если а — предел последовательности, то пишут или при .

С помощью логических символов это определение можно записать в виде:

Определение 2. Последовательность, у которой существует предел, называют сходящейся. Таким образом, последовательность {x_n} является сходящейся, если

Последовательность, не являющуюся сходящейся, называют расходящейся; иначе говоря, последовательность называют расходящейся, если никакое число не является ее пределом.

Заметим, что если x_n = a для всех n∈N(такую последовательность называют стационарной), то

Из определения (1) следует, что последовательность {x_n} имеет предел, равный a, тогда и только тогда, когда последовательность {x_n - а} имеет предел, равный нулю, т. е.:

Единственность предела последовательности.

Теорема 1. Числовая последовательность может иметь только один предел.

Доказательство:

►Предположим, что последовательность {x_n} имеет два различных предела a и b, причем a<b.

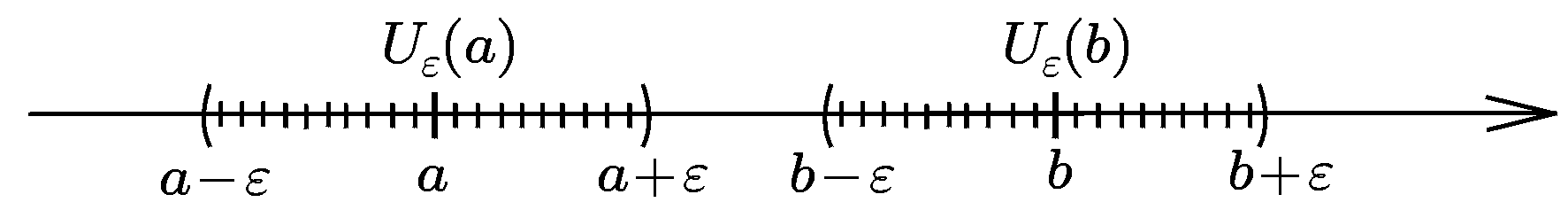
Выберем ε > 0 таким, чтобы ε-окрестности точек а и b не пересекались (не имели общих точек). Возьмем, например, ε = (b - a)/3. Так как число a — предел последовательности {x_n}, то по заданному ε > 0 можно найти номер N такой, что {x_n} ∈U_ε(a) для всех n∈N. Поэтому вне интервала U_ε(a) может оказаться лишь конечное число членов последовательности. В частности, интервал U_ε(b) может содержать лишь конечное число членов последовательности. Это противоречит тому, что b — предел последовательности (любая окрестность точки b должна содержать бесконечное число членов последовательности). Полученное противоречие показывает, что последовательность не может иметь два различных предела. Итак, сходящаяся последовательность имеет только один предел. ◄

Ограниченность сходящейся последовательности. Последовательность {x_n} называется ограниченной снизу, если существует такое число C₁, что все члены последовательности удовлетворяют условию x_n≥ C₁, т. е.

Последовательность {x_n} называется ограниченной сверху, если:

Последовательность, ограниченную как снизу, так и сверху, называют ограниченной, т. е. последовательность {x_n} называется ограниченной, если:

(5)

Таким образом, последовательность называют ограниченной, если множество ее значений ограничено.

Замечание 1. Условие (5) равносильно следующему:

В самом деле, из условия (6) следует(5), если взять С₁ = -С, С₂ = С, в из условия (5) следует (6), если взять С = max(|C₁|, |C₂|).

Геометрически ограниченность последовательности означает, что все члены последовательности содержатся в С-окрестности точки нуль.

Теорема 2. Если последовательность имеет предел, то она ограничена.

Доказательство:

►

Пусть последовательность {x_n} имеет предел, равный a. По определению предела для ε = 1 найдем номер N такой, что при всех n≥N имеет место неравенство |x_n - a|<1. Так как модуль суммы не превосходит суммы модулей, то

Поэтому при всех n>N выполняется неравенство

Положим c=max(1+|a|,|x₁|,…,|x_N-1|), тогда |xn|≤C при всех n∈N, т.е. последовательность {x_n} ограничена. ◄

Замечание 2. В силу теоремы 2 всякая сходящаяся последовательность является ограниченной. Обратное неверно: не всякая ограниченная последовательность является сходящейся. Например, последовательность {(—1)ⁿ} ограничена, но не является сходящейся

Замечание 3. Если условие (6) не выполняется, т. е.

то говорят, что последовательность {x_n} не ограничена.