Главное значение интегралов 2-го рода.
Пусть f(x)
определена на
 ,
за исключением может быть одной точки
(внутренней точки
,
за исключением может быть одной точки
(внутренней точки
 ).
).
 .
.
Кроме того, пусть
для
 ,
,
 ,
,
 .
Тогда под главным значением (V.p.)
понимается следующий предел
.
Тогда под главным значением (V.p.)
понимается следующий предел
 .
.
Билет № 21. Интегралы, зависящие от параметра
Интеграл, зависящий от параметра — математическое выражение, содержащее определённый интеграл и зависящее от одной или нескольких переменных («параметров»).
Пусть
в двумерном пространстве задана
область ![]() ,
на которой определена функция
,
на которой определена функция ![]() двух
переменных. Пусть далее, .
двух
переменных. Пусть далее, .
![]()
Функция ![]() и
называется интегралом,
зависящим от параметра.
и
называется интегралом,
зависящим от параметра.
Свойства интеграла, зависящего от параметра:
1) Непрерывность
Пусть
функция
непрерывна в
области ![]() как
функция двух переменных. Тогда
функция
как
функция двух переменных. Тогда
функция ![]() непрерывна
на отрезке
непрерывна
на отрезке ![]() .
.
2) Дифференцирование под знаком интеграла
Пусть
теперь на области
непрерывна
не только функция
,
но и её частная производная ![]() .
.
Тогда ![]() ,
или, что то же самое,
,
или, что то же самое, 
3) Интегрирование под знаком интеграла
Если
функция
непрерывна
в области
,то
![]() ,
или, что то же самое:
,
или, что то же самое:
![]()
Билет № 22. Интегралы Эйлера
Бета – функция
B(p,q)
:= p-1(1-x)q-1dx
p-1(1-x)q-1dx
P<1, q<1
Г(p):= -xxp-1dx
-xxp-1dx
p<1 сходится при p>0, q>0 и является непрерывным от p до q.
Свойства:
1. Г(p+1)
= pГ(p)
=> Г(n+1)
= n!,
n |N
|N
2. (1) = 1 =>
3.

Билет №23. Определение и свойства двойного интеграла
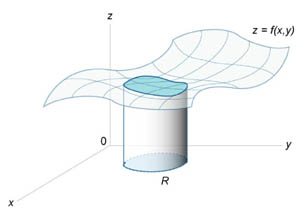
Определение двойного интеграла
Понятие интеграла может быть расширено на функции двух и большего числа переменных. Рассмотрим, например, функцию двух переменных z = f (x,y). Двойной интеграл от функции f (x,y) обозначается как
![]()
где R -
область интегрирования в плоскости
Oxy.
Если определенный интеграл ![]() от
функции одной переменной
от
функции одной переменной ![]() выражает
площадь под кривой f (x) в
интервале от x
= a до x
= b,
то двойной интеграл выражает объем под
поверхностью z
= f (x,y) выше
плоскости Oxy в
области интегрирования R (рисунок
1).
выражает
площадь под кривой f (x) в
интервале от x
= a до x
= b,
то двойной интеграл выражает объем под
поверхностью z
= f (x,y) выше
плоскости Oxy в
области интегрирования R (рисунок
1).
|
|
|
Рис.1 |
|
Рис.2 |
Формально
двойной интеграл можно ввести как
предел суммы
Римана.
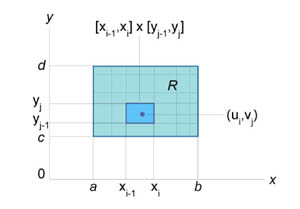
Пусть, для простоты, область
интегрирования R представляет
собой прямоугольник ![]() (рисунок
2).
(рисунок
2).
Двойной интеграл от функции f (x,y) в прямоугольной области определяется как предел суммы Римана, при котором максимальные значения Δxi и Δyj стремятся к нулю:
![]()
Чтобы определить двойной интеграл в произвольной области R, отличной от прямоугольной, выберем прямоугольник , покрывающий область R (рисунок 3), и введем функцию g (x,y), такую, что

Тогда двойной интеграл от функции f (x,y) в произвольной области R определяется как
![]()
Свойства двойного интеграла
Двойной интеграл обладает следующими свойствами:
 ,
где k -
константа;
,
где k -
константа;
Если
 в
области R,
то
в
области R,
то  ;
;
Если
 в
области R и
в
области R и  (рисунок
4), то
(рисунок
4), то  ;
;
Если на R и области R и S являются непересекающимися (рисунок5), то
 .
Здесь
.
Здесь  означает
объединение этих двух областей.
означает
объединение этих двух областей.
Билет №24.Сведение двойного интеграла к повторному:
-случай прямоугольной формы интегрирования (с доказательством)
-случай криволинейной трапеции
Сведение двойного интеграла к повторному.





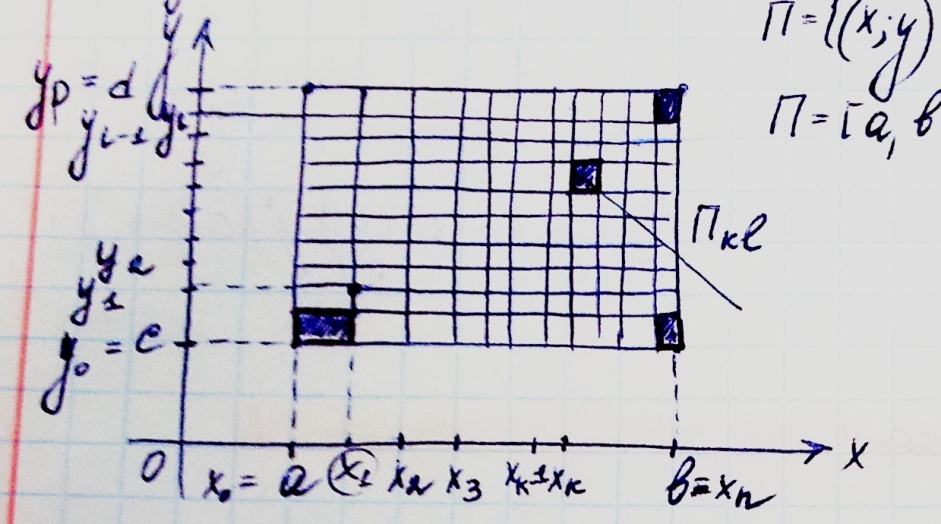
Теорема:
Пусть
f интегр по Риману на пр-нике П
Тогда
повторный интеграл


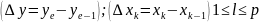













Замечание:
Пусть

Тогда
повторн интеграл



Криволинейная трапеция


Теорема
Пусть

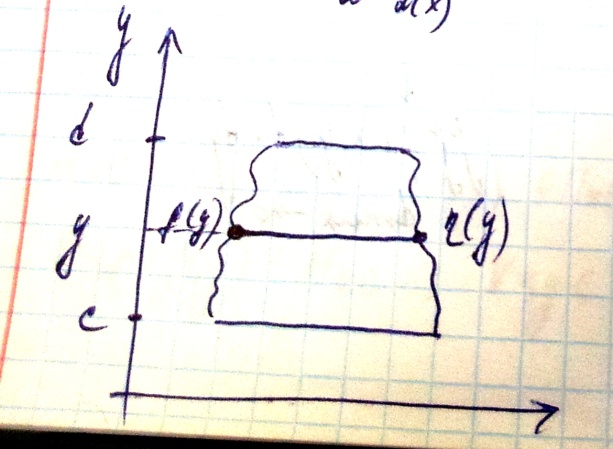
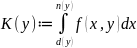




Билет №25. Тройные интегралы – теорема о сведении к повторным интегралам
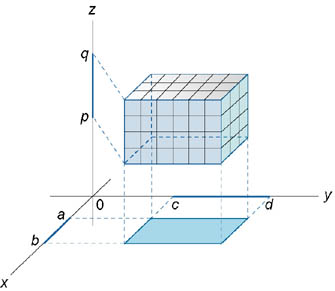






Свойство:
 - объем области D
- объем области D
Теорема о сведении тройного интеграла к повторному.
Пусть
 ,
,
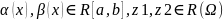
Тогда

Билет №26.Геометрический смысл модуля якобиана в двумерном случае
Определение:
Якобианом отображением F
в точке p=(u,v)
называется следующий определитель: =
=

Предположение:

 - геометрический смысл Якобиана
- геометрический смысл Якобиана
 при h->0
при h->0


Билет №27:Замена переменных в двойном интеграле
Замена переменных в двойном интеграле описывается формулой:
![]()
Теорема:
Пусть D, -
открытые, квадрируемые, ограниченные
-
открытые, квадрируемые, ограниченные
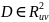 ,
,

F: x=x(u,v), y=y(u,v)- непрерывно и взаимнооднозначно отображает D на
F
непрерывно отображает замыкание
 на замыкание
на замыкание
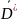
 – непрерывные
функции
для
– непрерывные
функции
для

Тогда

Билет №28: Полярные координаты, геометрический смысл якобиана в этом случае
F:
 - полярные координаты
- полярные координаты
Модуль
якобиана отображения равен ![]() .
Таким образом получаем, что
.
Таким образом получаем, что
![]() .
.
З десь
десь ![]() является
элементом площади в полярных координатах.
является
элементом площади в полярных координатах.
Переход из прямоугольных координат в полярные.

Билет №29: Геометрический смысл Якобиана в трехмерном случае.
Определение: Якобианом отображением F в точке t=(t1,t2,t3) называется следующий определитель


Билет № 30. 3амена переменных в тройном интеграле
Теорема:
Пусть: 1) Обл. Dx,
Dt
– кубируемых (измеряемые) откр, огр.

2) x
= F(t)
= {xj=xi(t1,
t2,
t3),
i=1,2,3}
Является непрерывной на
 ,
F
непрерывно отображает
на
,
F
непрерывно отображает
на
 взаимно однозначно и непрерывно диффер.
на отобра.
взаимно однозначно и непрерывно диффер.
на отобра.
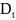 на
на

3) Якобиан
 на Dt
на Dt
J(t) непрерывно продолжим на
4) f(x)∈ C( ) (черта однозначное замыкание)
Тогда:


Билет №31. Сферические координаты, якобиан перехода от декартовых координат к сферическим
0≤θ≤π
0≤φ≤2π
0≤r≤+∞
θ, φ, r – сферические координаты
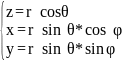

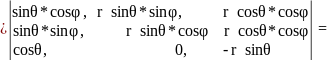




П осчитаем
этот интеграл с помощью полярных
координат
осчитаем
этот интеграл с помощью полярных
координат
0≤φ<2π
0
φ
≤r<-∞x=r cosφ
y=r cosφ
J2
=



Билет №32. Цилиндрические координаты, якобиан перехода от декартовых координат к цилиндрическим
Цилиндрические координаты,
Возьмем точку М
Соед. С нач. коорд.
Спроецир ее на oxy
Соед .
 с нач координат
с нач координатБерем плоскость м\у oz b om
Опускам перпендикуляр из М к oz
Z=h , O
 обознач. Через
p
обознач. Через
p
Опускаем перендикуляр
из
к Ox,
x=p
 =
= = 1
= 1 p=p
p=p
якобиан перехода от декартовых координат к цилиндрическим
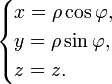
Билет №33. Замена переманных в n-кратном интеграле
 и
и
 - измеримые открытые множества
- измеримые открытые множества
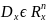 ,
,
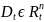
2)x=F(t)=x(t)= (x1, x2,…, xn) xi=xi(t1,…, tn)
t- вектор с координатами (t1, t2,…., tn), i1, i2,…
F: взамно-однозначно
взамно-однозначно
F непрерывнодефференцируема на
Обозначим
Fϵ (
),
т.е. все
(
),
т.е. все
 ϵ
C(
)
для любого 1≤I
, j≤h,
ϵ
C(
)
для любого 1≤I
, j≤h,
3)
J(t)= =
= не
равно 0 на
не
равно 0 на
4) J(t) непрерывно продолжим на тогда
Для
любого fϵC( )
справедлива формула
)
справедлива формула
 =
=
 =
=
Билет №34.Криволинейные интегралы первого и второго рода: определения, свойства (случай плоской кривой)
Определение:
Если существует конечный предел
интегральной суммы ![]() ,
не зависящий ни от способа разбиения
кривой на отрезки, ни от выбора точек
Mi, то он называется криволинейным
интегралом первого рода от функции f
по кривой L и обозначается
,
не зависящий ни от способа разбиения
кривой на отрезки, ни от выбора точек
Mi, то он называется криволинейным
интегралом первого рода от функции f
по кривой L и обозначается
![]()
Свойства
Линейность:
![]()
Аддитивность: если
 в
одной точке, то
в
одной точке, то
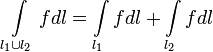
Монотонность: если
 на
на 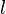 ,
то
,
то
![]()
Теорема о среднем для непрерывной вдоль функции
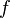 :
:
![]()
Очевидно,
что: ![]() .
.
5.
Изменение направления обхода кривой
интегрирования не влияет на знак
интеграла: ![]() .
.
6. Криволинейный интеграл первого рода не зависит от параметризации кривой.
Определение:
Если существует конечный предел
при ![]() интегральной
суммы
интегральной
суммы ![]() ,
не зависящий от способа разбиения
кривой на отрезки и выбора точек Mi, то
от называется криволинейным интегралом
второго рода от функции f(M) по кривой L
и обозначается
,
не зависящий от способа разбиения
кривой на отрезки и выбора точек Mi, то
от называется криволинейным интегралом
второго рода от функции f(M) по кривой L
и обозначается
![]() .
.
Свойства
1. Линейность:
![]()
2. Аддитивность:
![]()
3.
Монотонность: если
на ![]() ,
то
,
то
![]()
4. Оценка модуля:
![]()
Теорема о среднем: если непрерывна на , то
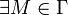 ,
такая что:
,
такая что:  6.
6. 
Билет №35. Формулы для вычисления криволинейных интегралов (случай плоской кривой, случай пространственной кривой)
Случай плоской кривой:
Криволинейный
интеграл 1-го рода при задании кривой
уравнениями ![]() ,
, ![]() (плоская
кривая) вычисляется по формуле
(плоская
кривая) вычисляется по формуле
![]()
При
явном задании кривой К уравнением
![]() криволинейный
интеграл второго рода вычисляется по
формуле
криволинейный
интеграл второго рода вычисляется по
формуле
![]()
т.е. криволинейный интеграл преобразуется в обыкновенный по х.
Случай пространственной кривой:
Криволинейный
интеграл первого рода по пространственной
кривой от функции трех переменных f (x,
у, z),
если кривая задана
уравнениями x = x(t), y = y(t), z = z(t),![]() ,
вычисляется по формуле
,
вычисляется по формуле
![]()
Вычисление криволинейного интеграла 2-го рода по пространственной кривой K; если кривая задана уравнениями x = x(t), y = y(t), z = z(t), где , проводится по формуле
![]()
![]()
Билет №36. Связь между криволинейными интегралами 2 рода и 1 рода(случай плоской кривой)
L:

L-гладкая кривая, без особых точек
P,Q
 C(L)
C(L)
 =
=
 =
=
 (t)=>
(t)=>
 =tgα
=tgα
M0M=( ,
,
τ=( )
)
τ(cosα, cosβ)
F=(P,Q) , τ=(cosα, cosβ)
I1=

I2=

Билет №37.Форма записи интеграла 2 рода с использованием направляющих косинусоидов касательной (случай плоской кривой, случай пространственной кривой)
Плоский случай
Пусть дан криволинейный интеграл второго рода по плоской кривой
![]() .
.
Ответ на поставленный вопрос дают следующие две теоремы.
Теорема
1. Для
того чтобы не зависел от пути
интегрирования необходимо и достаточно,
чтобы существовала такая функция ![]() ,
что
,
что
.![]()
Теорема
2. Если
в односвязной области существуют и
непрерывны  и
и ![]() ,
то для того, чтобы было выполнено условие
теоремы 1, необходимо и достаточно,
чтобы
,
то для того, чтобы было выполнено условие
теоремы 1, необходимо и достаточно,
чтобы
 .
.
Пространственный случай
В случае интегралов по пространственной кривой соответствующие теоремы приобретают следующий вид.
Теорема
1. Для
того чтобы ![]() не
зависел от пути интегрирования необходимо
и достаточно, чтобы существовала такая
функция,
не
зависел от пути интегрирования необходимо
и достаточно, чтобы существовала такая
функция, ![]() что
что ![]() .
.
Для
формулировки второй теоремы введем
понятие ротора векторной
функции. Пусть ![]() .
Тогда ротор этой функции определяется
так:
.
Тогда ротор этой функции определяется
так:

![]()
Теорема 2. Для того чтобы не зависел от пути интегрирования необходимо и достаточно, чтобы выполнялось условие
![]() .
.
Билет №38 и 39. Интегральная формула Грина. Доказательство формулы Грина в случае элементарной области относительно оси Ох.Применение формулы Грина для вычисления площадей
Пусть функции P(x,y), Q(x,y), P'y(х,у), Q'x(х,у) непрерывны в замкнутой области D, ограниченной контуром L .
Пусть контур L, кроме того, пересекается прямыми, параллельными осям координат, не более чем в двух точках. Пусть уравнение АСВ есть y = y1(x) при a ≤ x ≤ b , и уравнение АКВ есть y = y2(x) при a ≤ x ≤ b. Преобразуем двойной интеграл:

здесь
символ
![]() означает
криволинейный интеграл по замкнутому
контуру L.
означает
криволинейный интеграл по замкнутому
контуру L.
Аналогично
получается
![]()
Вычитая из формулы (3.9) формулу (3.8), получаем формулу Грина
![]()
В
формулах (3.8), (3.9) и (3.10) направление
обхода контура - положительное (против
часовой стрелки), т. е. область D
при движении по контуру L
всё время остается слева. С помощью
формулы Грина (3.10) можно получить
выражения площади плоской фигуры через
криволинейный интеграл по контуру этой
ф игуры.
Для этого достаточно подобрать P(x,y)
и Q(х,y) такими,
чтобы в области D
выполнялось условие
игуры.
Для этого достаточно подобрать P(x,y)
и Q(х,y) такими,
чтобы в области D
выполнялось условие
![]()
тогда двойной интеграл в формуле (3.10) будет давать величину S площади области D.
Билет №40. Условия, обеспечивающие независимость криволинейного интеграла второго рода от пути интегрирования (случай плоской кривой – с доказательством, случай пространственной кривой)

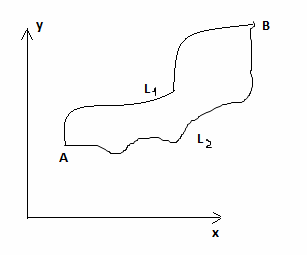


Рассмотрим
 ,
,
 ,
,
 .
.
1)
 ,
,
 .
.
Определение. Ф-ия
 называется
потенциалом поля
,
если
называется
потенциалом поля
,
если
 .
.
 .
.
 .
.
2)

 .
.
Билет №41. Критерий потенциальности поля в ограниченной односвязной области из плоскости (с доказательством)
Теорема. Пусть
область D-ограниченная,
односвязная,
 .
.
 .
Тогда любые пары точек
.
Тогда любые пары точек
 из D
из D
 не зависит от кусочно-гладкой кривой,
соединяющей точки A
и B,
тогда и только тогда, когда поле
=(P,Q)
потенциально. При этом
не зависит от кусочно-гладкой кривой,
соединяющей точки A
и B,
тогда и только тогда, когда поле
=(P,Q)
потенциально. При этом
 .
.
Теорема 2. Пусть
область D
– ограниченная, односвязная, открытая,
.
P,Q,
 .
Тогда поле является потенциальным в
области D
тогда и только тогда, когда
.
Тогда поле является потенциальным в
области D
тогда и только тогда, когда

 .
.
 .
.

 .
.

 Тогда поле
потенциально.
Тогда поле
потенциально.
 .
.
Пример.
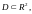
 ,
,
 .
.
 .
.
Билет №42.Критерий потенциального поля в трехмерном случае
Билет №43.Определение поверхностного интеграла первого рода. Вычисление поверхностного интеграла первого рода в случае явного уравнения для поверхности
Поверхностный
интеграл первого рода является таким
же обобщением двойного интеграла, как
криволинейный интеграл п ервого
рода по отношению к определённому
интегралу.
ервого
рода по отношению к определённому
интегралу.
Пусть S - поверхность в трёхмерном пространстве Oxyz, а F(x,y,z) - непрерывная функция, определённая в точках этой поверхности. Поверхность S сетью линий разобьём на n участков ΔS1, ΔS2, ...., ΔSi, ..., ΔSn, не имеющих общих внутренних точек (рис. 3.8). Площади "элементарных" участков обозначим теми же буквамиSi(i = 1,...,n), а наибольший из диаметров этих участков - через λ На каждом "элементарном" участке ΔSi произвольным образом выберем по точке Mi(xi,yi,zi) (i = 1,...,n) и составим сумму

которая называется интегральной суммой для функции F(x,y,z) по поверхности S.
Определение. Если существует конечный предел

не
зависящий от способа разбиения
поверхности S на
"элементарные" участки ΔSi и
от выбора точек Mi![]() ΔSi(i=1,....n),
то он называется поверхностным
интегралом первого рода от функции
f(x,y,z) по поверхности S и
обозначается
ΔSi(i=1,....n),
то он называется поверхностным
интегралом первого рода от функции
f(x,y,z) по поверхности S и
обозначается

Вычисление поверхностных интегралов первого рода обычно производится путём их сведения к двойным интегралам
.
Билет №44: Определение поверхностного интеграла второго рода, связь с поверхностным интегралом первого рода
Поверхностный
интеграл второго рода от
векторного поля ![]() по
ориентированной поверхности S (или
поток векторного
поля
через
поверхность S)
может быть записан в одной из следующих
форм:
по
ориентированной поверхности S (или
поток векторного
поля
через
поверхность S)
может быть записан в одной из следующих
форм:
Если поверхность S ориентирована внешней нормалью, то
![]()
Если поверхность S ориентирована внутренней нормалью, то

Величина ![]() называется векторным
элементом поверхности.
Точка обозначает скалярное произведение
соответствующих векторов. Частные
производные, входящие в последние
формулы, вычисляются следующим образом:
называется векторным
элементом поверхности.
Точка обозначает скалярное произведение
соответствующих векторов. Частные
производные, входящие в последние
формулы, вычисляются следующим образом:

Связь с поверхностным интегралом первого рода:
Интеграл
от ![]() -формы
-формы ![]() по
множеству
по
множеству ![]() в
стандартно ориентированном пространстве
в
стандартно ориентированном пространстве ![]() с
формой объема
с
формой объема ![]() определяется
равенством
определяется
равенством
|
|
При
изменении ориентации ( ![]() )
интеграл меняет знак.
)
интеграл меняет знак.
Интеграл
от ![]() -формы
-формы ![]() по
ориентированной
-мерной
поверхности
по
ориентированной
-мерной
поверхности ![]() с
параметризацией
с
параметризацией ![]() определяется
равенством
определяется
равенством
|
|
Интеграл
от формы ![]() по
гиперповерхности
называется
потоком вектора
по
гиперповерхности
называется
потоком вектора ![]() через
поверхности
.
В трехмерном случае
через
поверхности
.
В трехмерном случае
|
|
где ![]() .
Равенство
.
Равенство
|
|
где ![]() --
вектор единичной нормали, согласованный
с ориентацией поверхности
,
устанавливает связь поверхностных
интегралов 2-го и 1-го родов.
--
вектор единичной нормали, согласованный
с ориентацией поверхности
,
устанавливает связь поверхностных
интегралов 2-го и 1-го родов.
Билет №45. Поток векторного поля.
Рассмотрим кусок
поверхности
![]() ,
заданной уравнением
,
заданной уравнением
![]() .
Пусть выполняется условие
.
Пусть выполняется условие
![]() ,
что означает, что в каждой точке
поверхности существует нормаль с
направляющим вектором
,
что означает, что в каждой точке
поверхности существует нормаль с
направляющим вектором ![]() .
Выберем одну из сторон поверхности
следующим образом: построим на поверхности
достаточно малый замкнутый контур, на
котором задано направление обхода.
Построим вектор нормали в точке
поверхности, лежащей внутри контура.
Если из конца вектора нормали обход
контура кажется происходящим против
часовой стрелки, то будем называть
сторону поверхности, обращенную к
вектору нормали положительной стороной.
Таким образом, будем рассматривать
ориентированную двухстороннюю
поверхность, а односторонние поверхности
лист Мебиуса, бутылку Клейна оставим
в покое. Потоком векторного поля
.
Выберем одну из сторон поверхности
следующим образом: построим на поверхности
достаточно малый замкнутый контур, на
котором задано направление обхода.
Построим вектор нормали в точке
поверхности, лежащей внутри контура.
Если из конца вектора нормали обход
контура кажется происходящим против
часовой стрелки, то будем называть
сторону поверхности, обращенную к
вектору нормали положительной стороной.
Таким образом, будем рассматривать
ориентированную двухстороннюю
поверхность, а односторонние поверхности
лист Мебиуса, бутылку Клейна оставим
в покое. Потоком векторного поля
![]() через
ориентированную поверхность называется
поверхностный интеграл по площади
поверхности (1-го рода)
через
ориентированную поверхность называется
поверхностный интеграл по площади
поверхности (1-го рода)
![]() ,
где -
,
где -
 единичный вектор нормали, направленный
в положительную сторону. Выбор
положительной стороны обычно диктуется
физическими условиями задачи.
единичный вектор нормали, направленный
в положительную сторону. Выбор
положительной стороны обычно диктуется
физическими условиями задачи.
Билет№46. Формула Остроградского-Гауса. Формула Стокса.
Формула Остроградского-Гауса.
![]()
где ![]() и
и ![]() —
дифференциалы объёма и поверхности
соответственно. В современной записи
—
дифференциалы объёма и поверхности
соответственно. В современной записи ![]() —
элемент объёма,
—
элемент объёма, ![]() —
элемент поверхности.
—
элемент поверхности. ![]() —
функции, непрерывные вместе со своими
частными производными первого порядка
в замкнутой области пространства,
ограниченного замкнутой гладкой
поверхностью.
—
функции, непрерывные вместе со своими
частными производными первого порядка
в замкнутой области пространства,
ограниченного замкнутой гладкой
поверхностью.
Формула Стокса
Пусть
на ориентируемом
многообразии ![]() размерности
размерности ![]() заданы
ориентируемое
заданы
ориентируемое ![]() -мерное подмногообразие
-мерное подмногообразие ![]() и дифференциальная
форма
степени
и дифференциальная
форма
степени ![]() класса
класса ![]() (
(![]() ).
Тогда, если граница подмногообразия
).
Тогда, если граница подмногообразия ![]() положительно
ориентирована, то
положительно
ориентирована, то
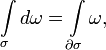
где ![]() обозначает
внешний дифференциал формы
.
обозначает
внешний дифференциал формы
.
Билет №47. Градиент. Дивергенция векторного поля, ротор векторного поля
Градиентом дифференцируемого скалярного поля u(M)=u(x,y,z) называется вектор
![]()
Дивергенцией
(или расходимостью) дифференцируемого
векторного поля
![]() называется
скаляр
называется
скаляр![]() .
.
Ротором
векторного поля![]() (M)
наз. вспомогательное векторное поле
rot
(M),
вектора которого в каждой точке
пространства определяют ориентацию
плоскости, в которой циркуляция вокруг
точки максимальна, а модуль ротора
|rot
(M)|
дает значение этой циркуляции.
(M)
наз. вспомогательное векторное поле
rot
(M),
вектора которого в каждой точке
пространства определяют ориентацию
плоскости, в которой циркуляция вокруг
точки максимальна, а модуль ротора
|rot
(M)|
дает значение этой циркуляции.
Ротор векторного поля (M) = {P, Q, R} удобно записывать в виде оператора
rot
(M) =
![]() x
(M)
=
x
(M)
=