Билет №1. Необходимое условие сходимости числового ряда с неотрицательными членами

Формулировка:

Если для числового ряда

с неотрицательными членами существует такое число  ,  , что, начиная с некоторого номера, выполняется неравенство  , то данный ряд сходится.

Предельная форма :

Условие радикального признака равносильно следующему:

То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:

Если для ряда , то если   ряд сходится, если   ряд расходится, если   вопрос о сходимости ряда остается открытым.

Доказательство:

1 случай. Пусть  .

Очевидно, что существует такое  , что  . Поскольку существует предел  , то подставив в определение предела выбранное   получим:

Раскрыв модуль, получаем: , ,

Поскольку  , то ряд   сходится. Следовательно ряд   тоже сходится

2 Случай. Пусть .

Очевидно, что существует такое  , что  . Поскольку существует предел  , то подставив в определение предела выбранное   получим:

Раскрыв модуль, получаем:

Поскольку  , то ряд   расходится. Следовательно ряд   тоже расходится.

Билет № 2. Обобщенный гармонический ряд с вещественным показателем р

Пусть даны два ряда   и  , у которых члены a_n и b_n положительны для всех n. Тогда справедливы следующие предельные признаки:

Если  , то оба ряда   и   либо сходятся, либо расходятся;

Если 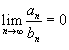 , то ряд   сходится, если сходится ряд  ;

Если 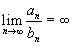 , то ряд   расходится, если расходится ряд  .

Так называемый обобщенный гармонический ряд   сходится при p > 1 и расходится при 0 < p ≤ 1. р это показатель.

Билет №3. Признаки сравнения для числовых рядов с неотрицательными членами

1. 

2. Все и

Предположим, что . Тогда, если сходится, то сходится

Если расходится, то расходится

сходится при α>1 и расходится при α≤1

сходится, если 0≤q≤1 и расходится, если q>1

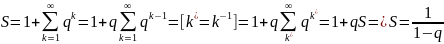
3. Все и

если сходится, то сходится

Если расходится, то расходится

Билет №4. Признак Даламбера для числовых рядов с положительными членами

, если q<1 , то сходится

Если q>1, то расходится

, , если

, то ряд сходится

, то ряд расходится

, то дополнительное исследование

Билет №5.Радикальный признак коши

Если , то ex

Если q>1, расх.

Если q=1?доп исследование

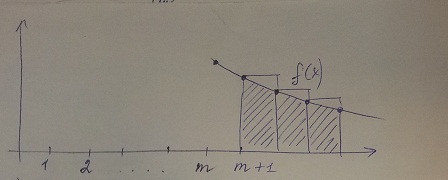
Билет №6.Интегральный признак сходимости ряда

f(x)

f(x)

тогда ряд (1)-сход

1) * <0

2)| | |<|

Билет №7 : Признак Лейбница для знакочередующихся числовых рядов

, 1) * ; 2) | | 0 , | | монотонно убывает, т.е. | |<| |

1)Sign =sign

2)| |<| |

Пусть интегральный признак Коши: (1), причем

Тогда ряд (1), (i) , если (i) сходится, то (1) сходится, если (i) расходится, то (1) расходится.

Билет № 8: Признаки Дирихле и Абеля для числовых рядов

Признак Дирихле:

(1)

1. монотонно стремится к 0

2. ограничена, т.е. Ǝ В>0: | |<B для любого n

Тогда ряд (1) сходится

Признак Абеля:

Пусть (1)

1. монотонна и ограничена

2. - сходится

Тогда ряд (1) сходится

Билет №9. Равномерная сходимость функциональных рядов

(1)

 — n-ная частичная сумма.

Определение: Будем говорить, что ряд (1) сходится поточечно (равномерно) к функции f(x) на множестве Х , если для ∀ х ∈ Х.

Сходимость

Ряд называется сходящимся поточечно, если последовательность его частичных сумм сходится поточечно.

Ряд называется сходящимся равномерно, если последовательность его частичных сумм сходится равномерно.

Необходимое условие равномерной сходимости

Билет №10. Признак Вейерштрасса равномерной и абсолютной сходимости функциональных рядов

(1)

Пусть ∀ n ∈ ℕ ∀ x ∈ X : | u_n(x)|≤α_n, где , тогда ряд (1) равномерно и абсолютно сходится

- сходится абсолютно

Билет № 11.Теорема о непрерывности суммы равномерно сходящегося ряда

Если члены функционального ряда   - непрерывные функции, и этот ряд равномерно сходится на отрезке  , то сумма этого ряда непрерывна на  .

Билет№12. Интегрирование и дифференцирование равномерно сходящегося функционального ряда

Интегрированиеравномерно сходящегося ряда

Тогда для любого ϵ[a,b] ряд равномерно сходится на отрезке [a,b] и имеет место формула =

дифференцирование равномерно сходящегося функционального ряда

: 1) ϵC[a,b] , (x)ϵ C[a,b]

2) равномерно сходится на [a,b]

3) сущ тогда ряд из сходится равномерно на отрезке [a,b] и его сумма

непрерывная на [a,b] и имеет место формула

Билет №13. Признаки Дирихле и Абеля равномерной сходимости функционального ряда

Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция  .

 — n-ная частичная сумма.