1.9. Алгебра событий.

Определение: Два события A и B называют равными и пишут A = B, если наступление события A влечёт за собой наступление события B, и, наоборот, наступление события B влечёт за собой наступление события A.

Пример: Брошены две игральные кости. Событие A – сумма выпавших на костях очков чётная, событие B – на костях чётности очков совпадают (т.е. на обеих костях выпало либо чётное, либо нечётное). Следовательно, A = B.

Определение: Объединением (или суммой) событий A и B называется событие, состоящее в наступлении события A или события B, или обоих этих событий.

Обозначается: или A + B. В случае объединения нескольких событий:

или A₁ + A₂ + … + A_k

Определение: Пересечением (или произведением) событий A и B называется событие, состоящее в одновременном наступлении как события A, так и события B.

Обозначается: или A·B. В случае объединения нескольких событий:

или A₁ · A₂ · …· A_k

Определение: Разностью событий A и B называется событие С, состоящее в том, что наступает событие A, но не наступает событие B.

С = A\B.

Определение: Противоположными называются два единственно возможных события, образующих полную группу.

Ā – событие, противоположное событию A.

Определение: Множество всех элементарных событий, которые могут появиться в испытании, называется пространством элементарных событий Ω:

Определение: Пространство элементарных событий Ω вместе с алгеброй событий F и вероятностью Р образует тройку (Ω, F, P), которая называется вероятностным пространством.

Определение: Если множество элементарных исходов Ω конечно или счетно, то соответствующее вероятностное пространство называется дискретным.

Напомним, что в теории множеств, счётное множество есть бесконечное множество, элементы которого возможно пронумеровать натуральными числами.

1.10. Теоремы сложения вероятностей.

Теорема 1: Вероятность суммы конечного числа несовместных событий A₁, A₂, …, A_n равна сумме вероятностей этих событий:

Доказательство: Докажем это равенство для суммы двух событий A₁+A₂, где A₁ и A₂ – несовместны.

Пусть событию A₁ благоприятствует m₁ элементарных исходов, а событию A₂ – m₂ элементарных исходов. Т.к. A₁ и A₂ – несовместны (A₁∩A₂=Ø), то событию A₁+A₂ благоприятствует m₁+m₂ элементарных исходов из общего числа n исходов. Тогда, получаем:

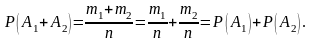
Для произвольного числа попарно несовместных событий доказательство проводится методом математической индукции.

Пример: Для отправки груза со склада может быть выделена одна из двух машин различного вида. Известны вероятности выделения каждой машины: P(A₁) = 0,2; P(A₂) = 0,4.

Тогда вероятность того, что к складу будет подана одна из этих машин, равна P(A₁+A₂) = 0,2 + 0,4 = 0,6.

Теорема 2: Сумма вероятностей попарно несовместных событий A₁, A₂, …, A_n, образующих полную группу, равна единице:

Доказательство: Т.к. появление одного из событий полной группы достоверно, а вероятность достоверного события равна единице, то P(A₁+A₂+…+A_n) = 1. Любые два события полной группы несовместны, тогда (по теореме 1) имеем:

Пример: Консультационный пункт института получает пакеты с контрольными работами из городов A, B и C. Вероятность получения пакета из города A равна 0,7, из города B – 0,2. Найти вероятность того, что очередной пакет будет получен из города C.

Решение: События «пакет получен из города A», «пакет получен из города B», «пакет получен из города C» образуют полную группу, следовательно:

0,7 + 0,2 + p = 1 => p = 1 – 0,9 = 0,1.

Теорема 3: Сумма вероятностей противоположных событий равна единице:

P(A) + P(Ā) = 1.

Доказательство: События A и Ā образуют полную группу, следовательно, по теореме 2 имеем:

Заметим, что при вычислении P(A) удобнее бывает вычислить P(Ā) и применить формулу:

Пример: В ящике находится 10 деталей, из которых 6 стандартных. Найти вероятность того, что среди четырех, наудачу извлечённых деталей, есть хоть одна стандартная.

Решение: Пусть событие A – «среди извлечённых деталей есть хоть одна стандартная». Тогда событие Ā – «среди извлечённых деталей нет ни одной стандартной».