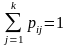5. Последовательности, образующие цепь Маркова.

А.А. Марков (1856 - 1922гг) – великий русский математик, ученик П.Л. Чебышёва, заложивший основы новой ветви теории вероятностей – теории случайных, или «стохастических» процессов.

Определение: Цепью Маркова называют последовательность испытаний, в каждом из которых появляется только одно из k несовместных событий А₁, А₂, …, А_k полной группы, причем условная вероятность р_ij(s) того, что в s-м испытании наступит событие A_j (j=1, 2, …, k), при условии, что в (s-1)-м испытании наступило событие A_i (i=1, 2, …, k), не зависит от результатов предшествующих испытаний.

Пример: Если последовательность испытаний образует цепь Маркова и полная группа состоит из четырех несовместных событий А₁, А₂, А₃, А₄, причем известно, что в шестом испытании появилось событие А₂, то условная вероятность того, что в седьмом испытании наступит событие А₄, не зависит от того, какие события появились в первом, втором, и т.д., в пятом испытаниях.

Заметим, что независимые испытания являются частным случаем цепи Маркова. Таким образом, понятие цепи Маркова является обобщением понятия независимых испытаний.

Пусть некоторая система в каждый момент времени находится в одном из k состояний: в первом, втором, и т.д., k-ом. В отдельные моменты времени в результате испытания состояние системы изменяется, то есть система переходит из одного состояния, например i, в другое, например j. В частности, после испытания система может остаться в том же состоянии («перейти» из состояния i в состояние j=i).

Таким образом, события называют состояниями системы, а испытания – изменениями её состояний.

Определение цепи Маркова можно дать в новой терминологии следующим образом.

Определение: Цепью Маркова называют последовательность испытаний, в каждом из которых система принимает только одно из k состояний полной группы, причем условная вероятность p_ij(s) того, что в s-ом испытании система будет находиться в состоянии j, при условии, что после (s-1)-го испытания она находилась в состоянии i, не зависит от результатов остальных, ранее произведенных испытаний.

Различают цепи Маркова с дискретным и непрерывным временем.

Определение: Цепью Маркова с дискретным временем называют цепь, изменение состояний которой происходит в определенные фиксированные моменты времени.

Определение: Цепью Маркова с непрерывным временем называют цепь, изменение состояний которой происходит в любые случайные возможные моменты времени.

Дадим еще два необходимых определения.

Определение: Цепь Маркова называют однородной, если условная вероятность p_ij(s) (перехода системы из состояния i в состояние j) не зависит от номера испытания.

Поэтому вместо p_ij(s) пишут просто p_ij.

Определение: Переходной вероятностью p_ij называют условную вероятность того, что из состояния i (в котором система оказалась в результате некоторого испытания, безразлично какого номера) в итоге следующего испытания система перейдет в состояние j.

Таким образом, в обозначении p_ij первый индекс i – номер предшествующего состояния, а второй индекс j – последующего.

– вероятность «перехода» из 1-го состояния в 1-ое;

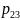– вероятность перехода из 2-го состояния в 3-е.

Пусть число состояний конечно и равно k.

Определение: Матрицей перехода системы называют матрицу, которая содержит все переходные вероятности этой системы: