2.2.1. Функция распределения вероятностей случайной величины.

Определение: Функцией распределения вероятностей (или кратко – функцией распределения) называется функция F(x), определяющая вероятность того, что случайная величина X в результате испытания примет значение, меньшее x ( ), т.е. F(x) = P(X < x).

Геометрический смысл: Функция распределения вероятностей F(x) – это вероятность того, что случайная величина X примет значение, которое изображается на числовой оси точкой, лежащей левее точки x.

Заметим, что F(x) – одна из форм задания закона распределения вероятностей. Это особенно важно для непрерывной случайной величины, которую нельзя задать в виде таблицы.

Теперь можно дать более точное определение непрерывной случайной величины.

Определение: Случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.

Рассмотрим основные свойства функции распределения:

Свойство 1: Значения функции распределения принадлежат отрезку [0, 1]:

Доказательство: Свойство вытекает из определения функции распределения как вероятности: вероятность – неотрицательное число, не превышающее единицы.

Свойство 2: Функция распределения вероятностей F(x) – неубывающая функция, т.е. F(x₂) ≥ F(x₁), если x₂ > x₁.

Доказательство: Пусть x₂ > x₁. Событие A = (X < x₂) можно подразделить на два несовместных события: X < x₁ с вероятностью P(X < x₁); x₁ ≤ X < x₂ с вероятностью P(x₁ ≤ X < x₂).

По теореме сложения несовместных событий имеем:

А это означает, что

Так как любая вероятность – число неотрицательное, то

Из этого свойства вытекают три следствия. Рассмотрим их.

Следствие 1: Вероятность того, что случайная величина примет значение, заключенное в промежутке [a, b), равна приращению функции распределения вероятностей на этом промежутке:

Доказательство: При x₂ = b, x₁ = a это утверждение вытекает из формулы .

Пример: Случайная величина X задана функцией распределения:

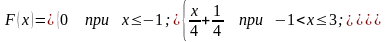
Найти вероятность того, что в результате испытания X примет значение, принадлежащее [0; 2), т.е.

Решение:

Следствие 2: Вероятность того, что непрерывная случайная величина X примет одно определённое значение, равна нулю.

Доказательство: Рассмотрим формулу

Положим a = x₁, b = x₁ + Δx, тогда получим:

Устремим Δx к нулю. Так как X – непрерывная случайная величина, то ее функция распределения F(x) непрерывна. В силу непрерывности F(x) в точке x₁ имеем:

Таким образом,

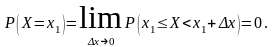
Следствие 3: Если X – непрерывная случайная величина, то:

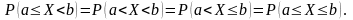
_{Доказательство:} Докажем, что

Разобьем интересующее нас событие на два несовместных события и воспользуемся теоремой о вероятности суммы несовместных событий:

Для непрерывной случайной величины вероятность попасть в точку равна нулю:

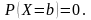
Тогда получаем

Аналогично доказываются остальные равенства.

Пример: На практике интересуются вероятностью того, что размеры деталей не выходят за дозволенные границы, но не ставят вопрос о вероятности их совпадения с проектным размером.

Заметим, что для непрерывной случайной величины факт P(X = x₁) = 0 не означает, что событие X = x₁ невозможно. В результате испытания случайная величина обязательно примет одно из возможных значений. В частности, это значение может оказаться равным x₁.

Свойство 3: Если возможные значения случайной величины принадлежат интервалу (a, b), то:

1) F(x) = 0 при x ≤ a;

2) F(x) = 1 при x ≥ b.

Доказательство: 1) Рассмотрим x₁ ≤ a. Тогда событие, состоящее в том, что X < x₁, невозможно, так как значения X принадлежат интервалу (a, b). Следовательно, P(X < x₁) = 0.

2) Рассмотрим x₂ ≥ b. Событие X < x₂ достоверно (т.к. все возможные значения X меньше x₂). Следовательно, P(X < x₂) = 1.

Из этого свойства, очевидно, вытекает следствие.

Следствие: Если возможные значения непрерывной случайной величины расположены на всей оси ОХ, то справедливы следующие предельные соотношения:

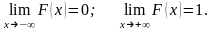
Доказанные свойства позволяют представить, как выглядит график функции распределения вероятностей непрерывной случайной величины.

Из первого свойства следует, что график расположен в полосе, ограниченной прямыми y = 0, y = 1.

Из второго свойства следует, что при увеличении x внутри интервала (a; b) график представляет собой график неубывающей функции.

Из третьего свойства следует, что при x ≤ a функция принимает нулевое значение (y = 0), а при x ≥ b функция равна единице (y = 1).

Таким образом, график функции распределения вероятностей F(x) непрерывной случайной величины может иметь вид:

График функции распределения вероятностей F(x) дискретной случайной величины имеет ступенчатый вид.

Если закон распределения вероятностей дискретной случайной величины задан в виде таблицы:

X
P

Если x ≤ x₁, то P(X < x) = 0 по свойству 3.

Если x₁ < x ≤ x₂, то P(X < x) = P(X = x₁) = p₁.

Если x₂ < x ≤ x₃, то по теореме о вероятности суммы несовместных событий P(X < x) = P(X = x₁) + P(X = x₂) = p₁ + p₂.

Если x₃ < x ≤ x₄, то P(X < x) = p₁ + p₂ + p₃.

Если x > x₄, то P(X < x) = 1, так как данное событие достоверно.

Тогда график функции распределения вероятностей F(x) имеет вид: