5.2.Групповая и общая средние.

Существуют понятия групповой и общей средней. Заметим, что под термином «группа» можно понимать также частичный интервал.

Пусть все значения количественного признака Х совокупности (генеральной или выборочной) разбиты на несколько групп. Рассматривая каждую группу, как самостоятельную совокупность, можно найти ее среднее арифметическое.

Определение: Групповой средней называется среднее арифметическое значений признака, принадлежащих группе.

Определение: Общей средней называется среднее арифметическое значений признака, принадлежащих всей совокупности.

Теорема: Общая средняя равна среднему арифметическому групповых средних, взвешенному по объемам групп.

Пример: Найти общую среднюю совокупности, состоящей из следующих двух групп:

Группа: №1 №2

Значение признака: 1, 6 1, 5

Частота: 10, 15 20, 30

Объем: 10+15=25 20+30=50

Решение: Найдем групповые средние:

Найдем общую среднюю по групповым средним:

Заметим, что для упрощения расчета общей средней совокупности большого объема целесообразно разбить эту совокупность на несколько групп, найти групповые средние и по ним вычислить общую среднюю.

5.3.Отклонение от общей средней и его свойство.

Рассмотрим отклонение от общей средней и его свойство. Пусть дана совокупность (генеральная или выборочная) объема n:

хi			…
			…

( далее для удобства записи будем использовать знак Σ). Найдем общую среднюю:

, тогда = (1)

Так как – постоянная величина, то

(2)

Определение: Отклонением называется разность х_i – между значением признака и общей средней.

Теорема: Сумма произведений отклонений на соответствующие частоты равна нулю: .

Доказательство: Учитывая формулы (1) и (2), имеем:

.

Что и требовалось доказать.

Следствие: Среднее значение отклонения равно нулю.

Действительно, = = 0.

Пример: Дано распределение количественного признака Х:

хi	1	2	3
ni	10	4	6

Убедимся, что сумма произведений отклонений на соответствующие частоты равна нулю.

Решение:

.

5.4.Генеральная и выборочная дисперсии.

Определение: Выборочной дисперсией называется среднее арифметическое квадратов отклонений значений признака выборочной совокупности от средней выборочной :

= , если х_i различны

или = средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.

Определение: Генеральной дисперсией D_г называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от генеральной средней :

D_г = , если х_i различны

или = – средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.

Пример: Генеральная совокупность задана таблицей распределения:

Xi	2	4	5	6
Ni	8	9	10	3

Найти D_г.

Решение: = = 4,

D_г = = 1,8.

Определение: Выборочным средним квадратическим отклонением или стандартом называется квадратный корень из выборочной дисперсии

=

Определение: Генеральным средним квадратическим отклонением или стандартом называется квадратный корень из генеральной дисперсии

= .

Теорема: Дисперсия (генеральная или выборочная) равна средней квадратов значений признака минус квадрат общей средней

D = – .

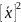Доказательство:

D = = = - 2 +

+ = - 2 - = - .

Что и требовалось доказать.

Пример: Найти дисперсию по данному распределению.

	1	2	3	4
ni	20	15	10	5

Решение:

= = 2

= = 5

D= - = 5 - 2² = 1.

Определение: Коэффициентом вариации V называется выраженное в процентах отношение выборочного среднего квадратического отклонения к выборочной средней:

Он служит для сравнения величин рассеяния двух вариационных рядов. Ряд, у которого коэффициент вариации больше, имеет большее рассеяние.