13.1.3.Корреляционная таблица.

При большом числе наблюдений одно и то же значение х может встретиться раз, одно и то же значение у может встретиться раз, одна и та же пара чисел (х,у) может наблюдаться раз. Поэтому данные наблюдений группируют, т.е. подсчитывают частоты .

Все сгруппированные данные записывают в виде таблицы, которую называют корреляционной.

Пример: Дана корреляционная таблица:

Y \ X	10	20	30	40
0,4	5	-	7	14	26
0,6	-	2	6	4	12
0,8	3	19	-	-	22
	8	21	13	18	n=60

Здесь наблюдаемые значения Х расположены по горизонтали: (10; 20; 30; 40). Наблюдаемые значения Y расположены по вертикали: .

На пересечении строк и столбцов находятся частоты наблюдаемых пар. Например, = 5 указывает на то, что пара значений (10; 0,4) наблюдалось 5 раз. Прочерк означает, что соответствующая пара значений не наблюдалась.

Не трудно вычислить частоты . Приведем два примера вычисления этих частот:

для Y = 0,4 = 5+7+14 = 26,

для Х = 10 = 5+3 = 8.

Указывается также n – сумма всех частот (общее число всех наблюдений n). Очевидно, что

.

В нашем примере:

.

13.1.4.Отыскание параметров выборочного уравнения линейной регрессии по сгруппированным данным.

Пусть получено большое число данных (для удовлетворительной оценки искомых параметров должно быть хотя бы 50 наблюдений), среди них есть повторяющиеся, и они сгруппированы в виде корреляционной таблицы.

Возьмём систему уравнений, полученную для определения параметров уравнения прямой линии регрессии Y на X:

(1)

Запишем систему (1) так, чтобы она отражала данные корреляционной таблицы:

, , ,

(учтено, что пара чисел (x, y) наблюдались раз).

Тогда, сократив на n, получим:

(2)

Решив эту систему, найдём параметры , тогда искомое уравнение линейной регрессии имеет вид:

(3)

Однако, более целесообразно, введя выборочный коэффициент корреляции, написать уравнение линейной регрессии в ином виде.

Из второго уравнения системы (2) следует Подставим это в уравнение в (3):

(4)

Найдём из системы (1) коэффициент регрессии, учитывая что :

(5)

Умножим обе части равенства (5) на дробь :

,

,

.

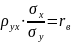Подставим найденный коэффициент в формулу (3) и получим выборочное уравнение линейной регрессии Y на X:

.

Аналогично находят выборочное уравнение линейной регрессии X на Y:

= ,

где

Следует заметить, что является оценкой коэффициента корреляции:

Действительно, используя метод моментов, т.е. заменив числовые характеристики их оценками, получим:

13.1.5.Выборочное корреляционное отношение.

Поставим вопрос: Как оценить тесноту любой корреляционной связи?

Пусть данные наблюдений над количественными признаками X и Y сведены в корреляционную таблицу. Можно считать, что тем самым наблюдаемые значения Y разбиты на группы. Каждая группа содержит те значения Y, которые соответствуют определенному значению X.

Пример: Дана корреляционная таблица

Y \ X	8	9
3	4	13
5	6	7
	10	20
	4,2	3,7

Здесь , таким образом:

К первой группе относятся те 10 значений Y (4 раза встречается значение и 6 раз – значение ), которые соответствуют значению .

Ко второй группе относятся те 20 значений Y, которые соответствуют значению .

Условные средние теперь можно назвать групповыми средними: групповая средняя первой группы ; групповая средняя второй группы . Так как все значения признака Y разбиты на группы, можно представить общую дисперсию признака в виде:

(1)

Докажем справедливость следующих утверждений:

1. Если признак Y связан с признаком X функциональной зависимостью, то .

2. Если признак Y связан с признаком X корреляционной зависимостью, то

Доказательство:

1. Если признак Y связан с признаком X функциональной зависимостью, то определенному значению X соответствует одно значение Y. В этом случае в каждой группе содержатся равные между собой значения Y. Следовательно, для каждой группы.

Например, если значению соответствует значение и , то в группе содержится 5 значений

Следовательно, средняя арифметическая групповых дисперсий (взвешенная по объемам групп), т.е. внутригрупповая дисперсия и формула (1) имеет вид: . Что и требовалось доказать.

2. Если признак Y связан с признаком X корреляционной зависимостью, то определенному значению X соответствуют различные значения Y (образующие группу).

В этом случае для каждой группы. Следовательно, средняя арифметическая групповых дисперсий, (взвешенная по объемам групп) . Тогда одно положительное слагаемое меньше суммы двух положительных слагаемых

=> < 1.

Что и требовалось доказать.

Уже из приведённых рассуждений видно, что чем связь между признаками X и Y ближе к функциональной, тем меньше и, следовательно, тем больше приближается к

Тогда дробь стремится к единице:

1.

Целесообразно, в качестве меры тесноты корреляционной зависимости рассматривать или .

Для оценки тесноты линейной корреляционной связи между признаками X и Y в выборке служит выборочный коэффициент корреляции. В случае нелинейной корреляции выборочный коэффициент корреляции утрачивает своё значение, как мера связи.

Для оценки тесноты нелинейной корреляционной связи вводятся новые сводные характеристики:

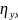– выборочное корреляционное отношение Y к X (греческая буква «эта»

– выборочное корреляционное отношение X к Y.

Определение: Выборочным корреляционным отношением признака Y к признаку X называется отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению признака Y:

или в других обозначениях

,

где n – объем выборки;

– частота значения x признака X;

частота значения y признака Y;

– общая средняя признака Y;

– условная средняя признака Y.

– межгрупповое среднее квадратическое отклонение.

– общее среднее квадратическое отклонение.

Аналогично определяется выборочное корреляционное отношение признака X к признаку Y:

Пример: По данным корреляционной таблицы найти

Y \ X	10	20	30
15	4	28	6	38
25	6	-	6	12
	10	28	12
	21	15	20

Решение: