30. Задача анализа и синтеза автоматов
По аналогии с задачей синтеза СФЭ можно
поставить задачу синтеза для автоматов.
Имеется неограниченный набор базисных
автоматов
.
Требуется собрать автомат
с наперед заданным функционированием.
При этом задача синтеза сталкивается
с определенными проблемами.
Допустим, что нужно присоединить выход
автомата
к входу автомата
.
Это возможно при условии
,
так как иначе второй автомат не поймет
сигналы, поступающие с первого. Это
приводит к запутанной ситуации, когда
некоторые соединения невозможны.
Чтобы преодолеть это препятствие, вводится понятие структурного автомата, в котором все алфавиты (входной, выходной и внутренних состояний) кодируются двоичными словами.
Пусть
– конечное множество из
элементов, а
– множество двоичных слов длины
,
где
.
Произвольное инъективное отображение
будем называть кодированием множества
двоичными словами.
Произведем кодирование алфавитов для произвольного автомата :
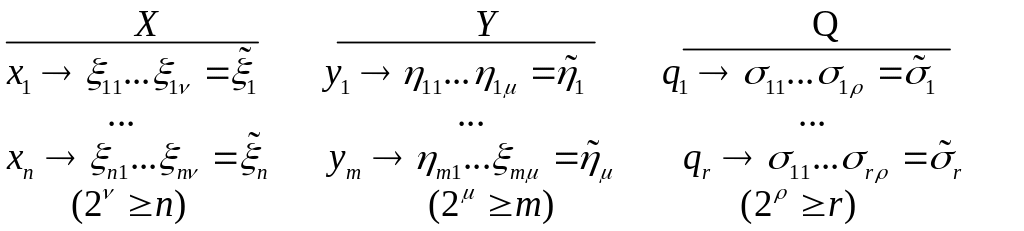
Обозначим закодированные вход, выход
и состояние автомата в момент времени
соответственно
.
Тогда закон функционирования представится
в виде
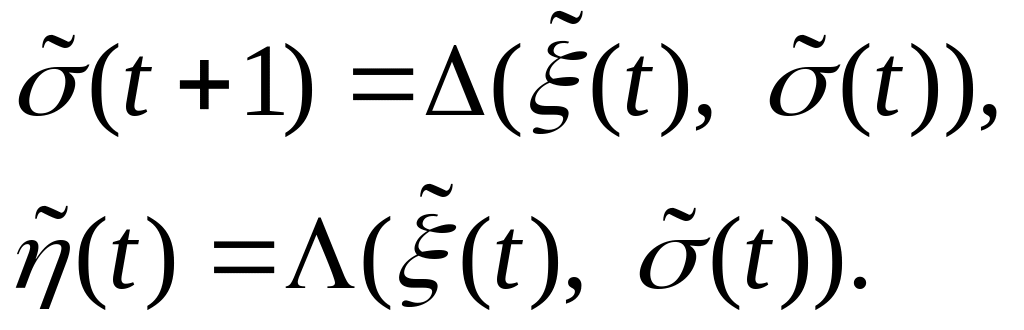(2)
Полученный после кодирования автомат
называют структурным. Будем считать,
что структурный автомат имеет
двоичных входов,
двоичных выходов, а внутреннее состояние
автомата задается двоичным словом длины
.
На рис. 3 показан абстрактный автомат
и соответствующий ему структурный
автомат.
…
…
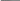
Рис. 3
Переход к структурному автомату обеспечивает два важных для синтеза преимущества.
1. Совместимость входов и выходов, так как через них передается двоичная информация. Мы не будем давать общее определение схемы из структурных автоматов – оно аналогично СФЭ.
2. Запишем соотношения (2) в «координатах»:
(3)
Из (3) следует, что закон функционирования структурного автомата задается системой булевых функций.
31.Элементарные автоматы
Выделим простейшие структурные автоматы и дадим им название.
Отметим сначала, что функциональный элемент, имеющий только одно состояние, можно рассматривать как автомат без памяти.
Перейдем к автоматам с двумя состояниями.
Пусть автомат имеет один двоичный вход
и один двоичный выход
,
совпадающий с внутренним состоянием:
:
Рис. 4.
Для задания автомата, показанного на рис. 4, достаточно задать только таблицу переходов:
Таблица 3
-
Вход
Состояние
0
1
0
*
*
1
*
*
Вместо звездочек нужно поставить 0 и 1. Это можно сделать 16 способами, однако, не все они приемлемы. Допустим, например, что в первом столбце таблицы 3 оба элементы нули. Такой автомат, оказавшись в состоянии 0, более из него не выйдет, то есть будет работать как функциональный элемент. Анализ аналогичный ситуаций показывает, что для того чтобы получился автомат, не сводящийся к автомату без памяти, надо потребовать, чтобы в каждом столбце таблицы 3 встречались и ноль и единица. Таких таблиц всего четыре.
Таблица 4 Таблица 5
-
Вход
Состояние
0
1
Вход
Состояние
0
0
0
0
1
1
1
1
0
0
1
1
1
0
Таблица 6 Таблица 7
-
Вход
Состояние
0
1
0
1
0
1
0
1
Вход |
Состояние |
|
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
Имеем только два простейших автомата, так как 7 получается из 4, а 6 из 5 путем инверсии внутренних состояний.
Автомат, задаваемый таблицей 4, называется
задержкой или
-триггером:
,
то есть этот автомат задерживает сигнал на один такт.
Автомат, задаваемый таблицей 5, называется
триггером со счетным входом или
-триггером.
Состояние автомата меняется на
противоположное, если на вход поступает
1, и остается без изменения, если на вход
поступает 0:
.
Пусть в начальный момент времени -триггер находится в состоянии 0. Если в некоторый момент времени -триггер находится в состоянии 0, то это означает, что на вход автомата поступило четное число единиц. Если в состоянии 1, то – нечетное. Таким образом, -триггер считает количество единиц на входе, но так как он имеет всего два состояния, то и считает до двух.
При физической реализации триггеров используют два выхода: прямой и инверсный (рис. 5). Если поменять их местами, то из -триггера получится автомат, задаваемый таблицей 7, а из -триггера – автомат, задаваемый таблицей 6.
Рис. 5.