25. Элементарные методы синтеза схем из функциональных элементов. Метод синтеза, основанный на более компактной реализации множества всех конъюнкций .

2. Метод синтеза, основанный на более компактной реализации множества всех конъюнкций .

На рис. 6 представлено индуктивное построение многополюсника ( ), реализующего множество всех конъюнкций . Имеем

,

,

.

_…

…

…

Базис индукции Индуктивный переход

Рис. 6

Для построения схемы, реализующей функцию , нужно в многополюснике отобрать выходы, соответствующие членам ее совершенной ДНФ , подключить их к схеме (см. рис. 3), осуществляющей логическое сложение, и удалить лишние элементы. Это потребует не более

элементов .

Таким образом, этот метод (алгоритм ) дает

.

26.Элементарные методы синтеза схем из функциональных элементов. Метод синтеза, основанный на разложении функции по переменной .

3. Метод синтеза, основанный на разложении функции по переменной .

для краткости положим

, .

На рис. 7 представлена индуктивная процедура построения схемы для .



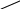
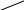
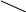
0 1

Базис индукции

Индуктивный переход

Рис. 7

На основании этого метода имеем алгоритм :

,

.

Окончательно имеем

.

Итак, мы видим, что построены алгоритмы и в некотором смысле дают возможность получить все более компактные реализации для функций и, в конечном счете, все более хорошие оценки для функций Шеннона. С другой стороны, получение более хороших результатов синтеза достигается за счет некоторого усложнения алгоритма.