
- •1. Введение
- •1) Задачи курса сопротивления материалов, реальный объект и расчетная схема.
- •2) Классификация тел по геометрическим параметрам (определения стержня, пластины, оболочки).
- •3) Классификация внешних сил.
- •4) Основные определения.
- •5)Перемещения
- •6) Деформации (абсолютные и относительные, продольные и поперечные).
- •7) Напряжения (нормальное и касательное напряжения), понятие о напряженном состоянии в точке.
- •8) Коэффициент запаса.
- •9) Общий вид условия прочности.
- •10) Внутренние силы. Метод сечений.
- •11) Основные гипотезы о свойствах материала.
- •12) Внутренние силовые факторы в стержне при центральном растяжении-сжатии.
- •13) Нормальные напряжения в поперечных и наклонных сечениях прямого стержня.
- •14) Гипотеза плоских сечений.
- •15) Продольные и поперечные деформации, коэффициент Пуассона.
- •16) Закон Гука при одноосном растяжении-сжатии.
- •17) Перемещения поперечных сечений стержня и его удлинение.
- •18) Построения эпюр продольных сил, нормальных напряжений и осевых перемещений на примере бруса.
- •19) Статически определимые и статически неопределимые задачи на растяжение-сжатие.
- •20)Температурные деформации и напряжения.
- •21) Экспериментальное определение механических характеристик материалов при центральном растяжении и сжатии. Механические характеристики материала.
- •22) Пластические и хрупкие материалы.
- •23) Закон разгрузки и повторного нагружения.
- •31) Осевые, полярные и центробежные моменты инерции.
- •32) Изменение моментов инерции при параллельном переносе и повороте осей координат.
- •33) Главные оси и главные моменты инерции.
- •34) Моменты инерции простых фигур.
- •35) Алгоритм определения положения центра тяжести сечения и вычисления моментов инерции для составных сечений. Применение понятий геометрических характеристик в расчетах.
- •4. Кручение
- •36)Понятие о чистом сдвиге.
- •37) Связь между модулями упругости первого и второго рода и коэффициентом Пуассона.
- •38) Кручение прямого стержня круглого поперечного сечения.
- •39) Угол закручивания
- •41) Построение эпюр крутящих моментов , касательных напряжений, и углового закручивания
- •42)Виды изгиба стержня
- •49) 54)Метод начальных параметров
42)Виды изгиба стержня
Изгиб называется плоским или прямым, если плоскость действия нагрузки проходит через главную центральную ось инерции сечения (рис.6.1).
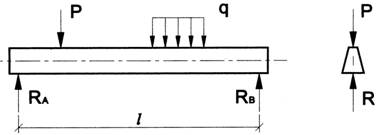
Рис.6.1
При
плоском поперечном изгибе в балке
возникают два вида внутренних усилий:
поперечная сила Q и
изгибающий момент M.
В раме при плоском поперечном изгибе
возникают три усилия:
продольная N, поперечная Q силы
и изгибающий момент M.Если
изгибающий момент ![]() является
единственным внутренним силовым
фактором, то такой изгиб
называется чистым (рис.6.2).
При наличии поперечной силы
является
единственным внутренним силовым
фактором, то такой изгиб
называется чистым (рис.6.2).
При наличии поперечной силы ![]() изгиб
называется поперечным.
Строго говоря, к простым видам сопротивления
относится лишь чистый изгиб; поперечный
изгиб относят к простым видам сопротивления
условно, так как в большинстве случаев
(для достаточно длинных балок) действием
поперечной силы при расчетах на прочность
можно пренебречь.
изгиб
называется поперечным.
Строго говоря, к простым видам сопротивления
относится лишь чистый изгиб; поперечный
изгиб относят к простым видам сопротивления
условно, так как в большинстве случаев
(для достаточно длинных балок) действием
поперечной силы при расчетах на прочность
можно пренебречь.
Косой изгиб - изгиб, при котором нагрузки действуют в одной плоскости, не совпадающей с главными плоскостями инерции.
Сложный изгиб - изгиб, при котором нагрузки действуют в различных (произвольных) плоскостях.
Далее будем рассматривать плоский изгиб, то есть все силы будем прилагать в плоскости симметрии балки.

43) Внутренние силовые факторы и дифференциальные зависимости при прямом поперечном изгибе
При действии на брус внешних нагрузок, расположенных на одной плоскости, проходящей через ось бруса, в каждом поперечном сечении возникают внутренние силовые факторы:
1) продольная сила приложена в центре тяжести сечения, действующая перпендикулярна к сечению; Продольная сила по величине и знаку равна сумме проекций всех внешних сил, приложенных к левой части бруса, на его продольную ось, или сумме проекций (на ту же ось), взятой с обратным знаком, всех внешних сил, приложенных к правой части бруса : Продольная сила в сечении положительна при растяжении и отрицательна при сжатии.
2) поперечная сила , действующая в плоскости поперечного сечения, проходящая через его центр тяжести; Поперечная сила в любом поперечном сечении балки равна сумме проекций всех действующих сил слева от сечения на ось, перпендикулярную оси балки и сумме проекций всех сил справа от сечения, но с обратным знаком. Поперечная сила имеет положительное значение, если относительно сечения она стремится повернуть балку по часовой стрелке (рис а), и отрицательное – если против часовой (рис б).
3) изгибающий момент ,действующий в плоскости, перпендикулярной к поперечному сечению. Изгибающий момент в любом сечении балки численно равен алгебраической сумме моментов, действующих на балку внешних сил, относительно центра тяжести этого сечения. Изгибающий момент имеет положительное значение, если он действует так, что ось балки изгибается выпуклостью вниз (рис а) и отрицательное – выпуклостью вверх (рис б).
![]() ,
,
![]() ,
,
![]() .
.
Интенсивность распределенной нагрузки равна первой производной по абсциссе сечения от поперечной силы или второй производной от изгибающего момента.
Поперечная сила в сечении равна первой производной от изгибающего момента по абсциссе сечения (теорема Д.И.Жуковского). Полученные зависимости используют при построении эпюр поперечных сил и изгибающих моментов.
44) Правила построения эпюр внутренних силовых факторов в балках
1) На участках балки, на которых поперечная сила положительна, изгибающий момент возрастает (слева направо), а на участках, на которых она отрицательна – убывает.
2) Чем больше по абсолютной величине значение поперечной силы , тем круче линия, ограничивающая эпюру .
3) На участке балки, на котором поперечная сила имеет постоянное значение, эпюра ограничена прямой линией.
4) Если на границе соседних участков балки эпюра не имеет скачка, то линии, ограничивающие эпюру на этих участках, сопрягаются без перелома, т.е имеют в точке общую касательную.
5) Если на границе соседних участков балки в эпюре имеется скачок, то линии, ограничивающие эпюру на этих участках, сопрягаются с переломом.
6) Изгибающий момент достигает максимума или минимума в сечениях балки, в которых поперечная сила равна нулю; касательная к линии, ограничивающей эпюру , в этом сечении параллельна оси эпюр.
7) На участках действия распределенной нагрузки поперечные силы изменяются по длине балки (если интенсивность постоянна, то поперечные силы изменяются по линейному закону).
8) На участках балки, на которых распределенная нагрузка отсутствует, поперечные силы постоянны, а изгибающие моменты меняются по линейному закону
Правило
знаков.
К рутящий
момент будем считать положительным,
если, идя слева или справа, он вращает
вал против хода часовой стрелки, и
отрицательным, если наоборот(рисунок
5.4).
Правила
построения эпюры Мкр:
1. Разбиваем
вал на грузовые участки.
2.
Обозначаем сечения 1 – 4.
3.Определяем
значения Мкр
j с
учетом правила знаков.
рутящий
момент будем считать положительным,
если, идя слева или справа, он вращает
вал против хода часовой стрелки, и
отрицательным, если наоборот(рисунок
5.4).
Правила
построения эпюры Мкр:
1. Разбиваем
вал на грузовые участки.
2.
Обозначаем сечения 1 – 4.
3.Определяем
значения Мкр
j с
учетом правила знаков.
45) Нормальные напряжения при чистом изгибе
При
плоском изгибе в общем случае возникают
внутренние
силовые факторы:
продольная сила N,
поперечная сила Q
и изгибающий момент М. N>0,
если продольная сила растягивающая;
при М>0 волокна сверху балки сжимаются,
снизу растягиваются.
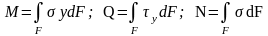 .
.
Слой,
в котором отсутствуют удлинения,
называется нейтральным
слоем (осью,
линией). При N=0
и Q=0,
имеем случай чистого
изгиба.
Нормальные напряжения:
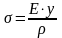 ,
— радиус кривизны нейтрального слоя,
y
— расстояние от некоторого волокна до
нейтрального слоя. Закон
Гука при изгибе:
,
— радиус кривизны нейтрального слоя,
y
— расстояние от некоторого волокна до
нейтрального слоя. Закон
Гука при изгибе:
 ,
откуда (формула Навье):
,
откуда (формула Навье):
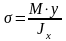 ,
Jx
— момент инерции сечения относительно
главной центральной оси, перпендикулярной
плоскости изгибающего момента, EJx
— жесткость при изгибе,
,
Jx
— момент инерции сечения относительно
главной центральной оси, перпендикулярной
плоскости изгибающего момента, EJx
— жесткость при изгибе,
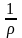 — кривизна нейтрального слоя.
— кривизна нейтрального слоя.
Максимальные
напряжения при изгибе возникают в
точках, наиболее удаленных от нейтрального
слоя:
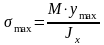 ,
Jx/ymax=Wx—момент
сопротивления сечения при изгибе,
,
Jx/ymax=Wx—момент
сопротивления сечения при изгибе,
 .
.
46) Нормальные и касательные напряжения при прямом поперечном изгибе Нормальные напряжения, возникающие при поперечном изгибе, с достаточной для практических целей точностью могут определяться по формулам чистого изгиба. Поэтому условия прочности по нормальным напряжениям имеют тот же вид, что и для чистого изгиба.
Касательные напряжения в поперечных сечениях балки появляются при нагружении балки сосредоточенными и распределенными силами. Величина их определяется формулой Журавского:
 ,
,
где ![]() -
поперечная сила,
-
поперечная сила,
![]() -
статический момент отсеченной части
сечения относительно нейтральной оси,
-
статический момент отсеченной части
сечения относительно нейтральной оси,
b - ширина сечения,
![]() -
осевой момент инерции.
-
осевой момент инерции.
Эпюра касательных напряжений показана на рис.6.6.
Условие прочности по касательным напряжениям будет иметь вид:
![]()
где ![]() -
наибольшая по модулю поперечная сила,
-
наибольшая по модулю поперечная сила,
- статический момент инерции верхней половины сечения.
Или это
Формулы
для определения нормального напряжения
для чистого изгиба приближенно годятся
и когда Q0.
Это случай поперечного
изгиба. При
поперечном изгибе, кроме изгибающего
момента М, действует поперечная сила
Q
и в сечении возникают не только нормальные
,
но и касательные
напряжения. Касательные напряжения
определяются формулой
Журавского:
 ,
где Sx(y)
— статический момент относительно
нейтральной оси той части площади,
которая расположена ниже или выше слоя,
отстоящего на расстоянии "y"
от нейтральной оси; Jx
— момент инерции всего
поперечного сечения относительно
нейтральной оси, b(y)
— ширина сечения в слое, на котором
определяются касательные напряжения.
,
где Sx(y)
— статический момент относительно
нейтральной оси той части площади,
которая расположена ниже или выше слоя,
отстоящего на расстоянии "y"
от нейтральной оси; Jx
— момент инерции всего
поперечного сечения относительно
нейтральной оси, b(y)
— ширина сечения в слое, на котором
определяются касательные напряжения.
Д ля
прямоугольного сечения:
ля
прямоугольного сечения:
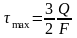 ,
F=bh,
для круглого сечения:
,
F=bh,
для круглого сечения: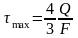 ,
F=R2,
для сечения любой формы
,
F=R2,
для сечения любой формы
 ,
,
k— коэфф., зависящий от формы сечения (прямоугольник: k= 1,5; круг - k= 1,33).
M max
и Qmax
определяются из эпюр изгибающих моментов
и поперечных сил. Для этого балка
разрезается на две части и рассматривается
одна из них.
max
и Qmax
определяются из эпюр изгибающих моментов
и поперечных сил. Для этого балка
разрезается на две части и рассматривается
одна из них.
Д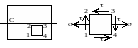 ействие
отброшенной части заменяется внутренними
силовыми факторами М и Q,
которые определяются из уравнений
равновесия. В некоторых вузах момент
М>0 откладывается вниз, т.е. эпюра
моментов строится на растянутых волокнах.
При Q=
0 имеем экстремум эпюры моментов
ействие
отброшенной части заменяется внутренними
силовыми факторами М и Q,
которые определяются из уравнений
равновесия. В некоторых вузах момент
М>0 откладывается вниз, т.е. эпюра
моментов строится на растянутых волокнах.
При Q=
0 имеем экстремум эпюры моментов
47)
Расчёт на прочность при изгибе
два условия прочности, относящиеся к
различным точкам балки: а) по нормальным
напряжениям
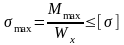 ,
(точки наиболее удаленные от С); б) по
касательным напряжениям
,
(точки наиболее удаленные от С); б) по
касательным напряжениям
 ,
(точки на нейтр.оси). Из а) определяют
размеры балки:
,
(точки на нейтр.оси). Из а) определяют
размеры балки:
 ,
которые проверяют по б). В сечениях балок
могут быть точки, где одновременно
большие нормальные и большие касательные
напряжения. Для этих точек находятся
эквивалентные напряжения, которые не
должны превышать допустимых. Условия
прочности проверяются по различным
теориям прочности
,
которые проверяют по б). В сечениях балок
могут быть точки, где одновременно
большие нормальные и большие касательные
напряжения. Для этих точек находятся
эквивалентные напряжения, которые не
должны превышать допустимых. Условия
прочности проверяются по различным
теориям прочности
I-я:
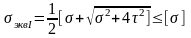 ;
II-я:
;
II-я: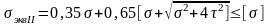 (при коэфф.Пуассона =0,3);
— применяются редко.
(при коэфф.Пуассона =0,3);
— применяются редко.
III-я: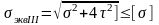 ,
IV-я:
,
IV-я: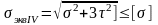 ,
,
теория
Мора:
 ,
,
 (используется для чугуна, у которого
допускаемое напряжение на растяжение
[р][с]
– на сжатие).
(используется для чугуна, у которого
допускаемое напряжение на растяжение
[р][с]
– на сжатие).
48)Определение перемещений при изгибе и Интегрирование дифференциального уравнения упругой линии
И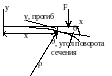 меем
закон Гука при изгибе:
меем
закон Гука при изгибе:
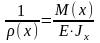 ,
где (х)
— радиус кривизны изогнутой оси балки
в сечении х, М(х) — изгибающий момент
в том же сечении, EJ
— жесткость балки. Из высшей математики
известно:
,
где (х)
— радиус кривизны изогнутой оси балки
в сечении х, М(х) — изгибающий момент
в том же сечении, EJ
— жесткость балки. Из высшей математики
известно:
 —
дифференциальное уравнение изогнутой
оси балки.
—
дифференциальное уравнение изогнутой
оси балки.
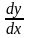 — тангенс угла между осью х и касательной
к изогнутой оси. Эта величина очень мала
(прогибы балки малы)
ее квадратом пренебрегают и угол поворота
сечения приравнивают тангенсу.
Приближенное дифференциальное
ур-ние изогнутой оси балки:
— тангенс угла между осью х и касательной
к изогнутой оси. Эта величина очень мала
(прогибы балки малы)
ее квадратом пренебрегают и угол поворота
сечения приравнивают тангенсу.
Приближенное дифференциальное
ур-ние изогнутой оси балки:
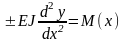 .
Если ось y
направлена вверх, то знак (+). В некоторых
вузах ось y
направляется вниз (—).
Интегрируя дифф. уравнение, получаем:
.
Если ось y
направлена вверх, то знак (+). В некоторых
вузах ось y
направляется вниз (—).
Интегрируя дифф. уравнение, получаем:
 — ур-ние
углов поворота,
интегрируем второй раз:
— ур-ние
углов поворота,
интегрируем второй раз:
 — получаем ур-ние
прогибов.
Постоянные интегрирования С и D
находятся из граничных условий, которые
зависят от способов закрепления балки.
— получаем ур-ние
прогибов.
Постоянные интегрирования С и D
находятся из граничных условий, которые
зависят от способов закрепления балки.
! то же есть в лекции, но в лекции попонятнее
