
- •Билет №10
- •Вопрос 11
- •Вопрос 12
- •Вопрос 13
- •Вопрос 14
- •Алгоритм определения линии пересечения двух плоскостей:
- •Вопрос 15
- •Вопрос 21. Линейчатые развертываемые поверхности
- •Поверхность с ребром возврата
- •Коническая поверхность
- •Цилиндрическая поверхность
- •Билет №22 Поверхности вращения общего вида
- •Билет №23 Линейчатые поверхности вращения
- •Проецирующие поверхности
- •Билет №25 Поверхности с плоскостью параллелизма (поверхности Каталана)
- •Цилиндроиды
- •Коноиды
- •Косая плоскость (гиперболический параболоид)
- •27. Пересечение поверхности плоскостью частного и общего положения. Алгоритм определения точек линии пересечения. Определение видимости и натуральной величины сечения.
- •28. Сечение поверхностей вращения. Сечения цилиндра, конуса, сферы плоскостями частного положения.
- •29. Пересечение прямой линии с поверхностью. Алгоритм определения точек линии пересечения. Определение видимости прямой.
Проецирующие поверхности
На комплексном чертеже задачи решаются проще, если цилиндрические и призматические поверхности занимают проецирующее положение, т.е. перпендикулярное одной из плоскостей проекций (см. рис.2). При таком положении поверхности одна из проекций образующей вырождается в точку, а проекция поверхности - в линию. Вырожденная проекция поверхности, подобно проецирующей плоскости, обладает «собирательным свойством»: проекция любой линии, расположенной на поверхности, находится на вырожденной проекции поверхности. На рис. 2 а, б показаны случаи, когда горизонтальная проекция поверхности «собирает» на себя все горизонтальные проекции точек, расположенных на поверхности; на рис. 2 в, г - случаи, когда фронтальные проекции поверхностей «собирают» на себя все фронтальные проекции точек, расположенных на поверхности. Принадлежность точек поверхности определяется в этом случае принадлежностью проекций точек вырожденной проекции поверхности.
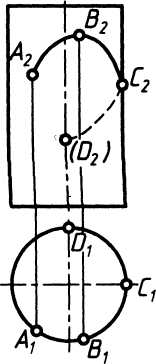
a)
Билет № 24
Нелинейчатые (криволинейные) поверхности вращения.
Такие поверхности имеют в меридиональном сечении кривую второго порядка или две прямые, на которые распадаются кривые второго порядка. По виду главного меридиана и расположению оси вращения поверхности вращения имеют разные названия. На рис. 1 представлена группа поверхностей, имеющих в качестве образующей кривую второго порядка, а в качестве оси вращения - проецирующую прямую m.
Рассмотрим подробнее эти поверхности.
Сфера. Это поверхность, образованная вращением окружности вокруг одного из своих диаметров. Ось вращения проходит через центр окружности. Уравнение поверхности: х2 + у2 + z2 = r2.
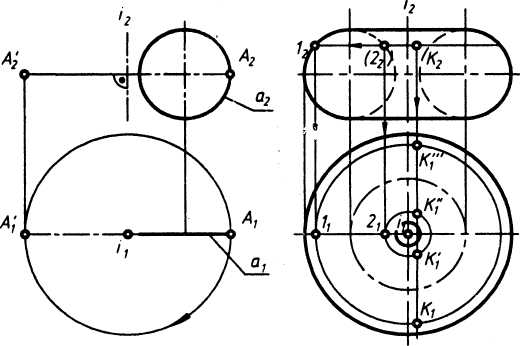
На рис. 2 дан комплексный чертеж сферы, заданной очерками. Пусть ось вращения - горизонтально-проецирующая прямая, тогда фронтальным очерком сферы будет фронтальная проекция главного меридиана а2, а горизонтальным очерком - горизонтальная проекция экватора b1. Для построения недостающих проекций К1 и К’ точек К и К’ расположенных на поверхности, используют параллель. Видимость точек на поверхности определяют на фронтальной плоскости проекций П2 меридианом, а на П1 -экватором сферы. Невидимыми будут точки за меридианом и под экватором.
Тор открытый (или круговое кольцо). Ось вращения не пересекает образующую окружность, но лежит в ее плоскости. Уравнение поверхности: (x2 + y2 +z2 + a2 –b2)2 =4a2(x2 + y2); где а>b
На рис. 3а дана геометрическая часть определителя кругового кольца. Зная, что каждая точка линии а описывает окружность, плоскость которой перпендикулярна оси i, а центр расположен на оси, можно построить очерки поверхности. На рис. 3б, заданы очерки этой поверхности. По фронтальной проекции точки К, расположенной на поверхности, строят горизонтальные проекции ее. Если известно, на видимой части поверхности расположена точка К или на невидимой, то можно проводить ее возможные параллели. В данном случае возможны две параллели, пересекающие образующую в двух точках 1 и 2, следовательно, при положении К2 на поверхности возможны четыре положения точек К1.
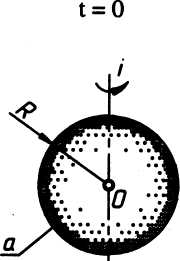
Тор закрытый. Ось вращения пересекает образующую окружность, но не проходит через ее центр (см. рис.1). Уравнение поверхности: (x2 + y2 +z2 + a2 –b2)2 =4a2(x2 + y2); где а<b
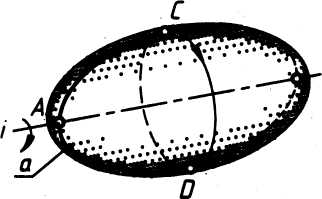
Эллипсоид вращения. Поверхность, образованная вращением эллипса вокруг своей оси. Поверхность, образованная вращением вокруг малой оси, называется сжатым эллипсоидом вращения (рис. 4 а), а вращением вокруг большой оси - вытянутым эллипсоидом вращения (рис. 4 б).
Уравнение сжатого эллипсоида: а2(х2 + у2) + b2z2 = a2b2.
Уравнение вытянутого эллипсоида: b2(х2 + у2) + a2z2 = a2b2.
Параболоид вращения. Поверхность, образованная вращение параболы вокруг ее оси (рис. 5). Уравнение поверхности: х2 + у2 = 2pz.
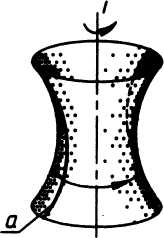
Гиперболоид вращения. Поверхность, образованная вращением гиперболы вокруг мнимой оси, называется однополостным гиперболоидом вращения (рис. 6 а). Поверхность, образованная вращением гиперболы вокруг ее действительной оси, называется двухполостным гиперболоидом вращения (рис. 6б).
Уравнение двухполостного гиперболоида вращения: b2z2 - a2 (х2 + у2) = a2b2.
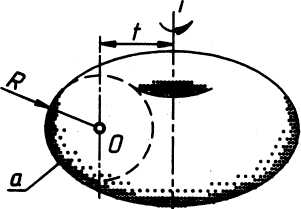
тор открытый
тор закрытый
сфера
эллипсоид вытынутый
Двухполосный
гиперболоид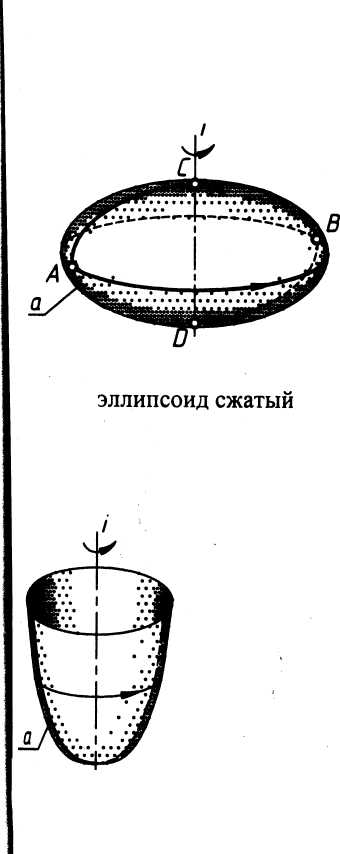
Гиперболоид
Рис. 1
Рис. 3
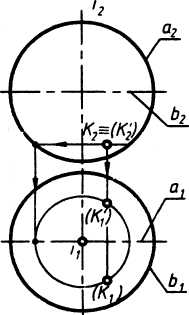
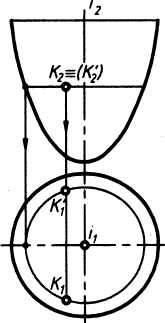
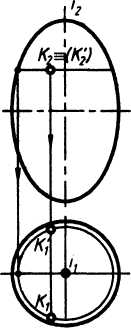
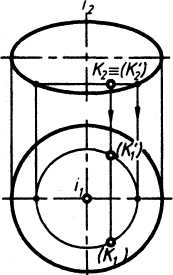
а) б)
Рис. 4 Рис. 5
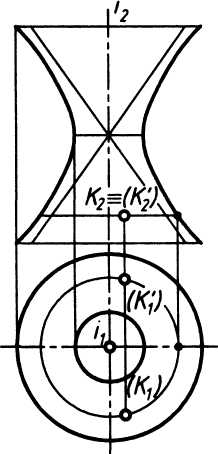
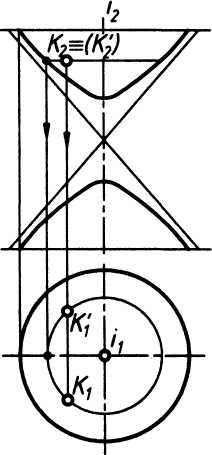
а) Рис. 6 б)
